2023-2024学年初中数学八年级上册 4.3 一元一次不等式的解法 同步分层训练基础卷(湘教版)
试卷更新日期:2023-12-11 类型:同步测试
一、选择题
-
1. 不等式的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、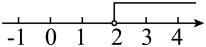 2. 关于x的不等式解集为 , 则a的值为( )A、2 B、 C、1 D、3. 以下是一元一次不等式的是( )A、 B、 C、 D、4. 若不等式的解集为 , 则的取值范围是( )A、 B、 C、 D、5. 如果式子 有意义,那么x的取值范围在数轴上表示出来,正确的是( )A、
2. 关于x的不等式解集为 , 则a的值为( )A、2 B、 C、1 D、3. 以下是一元一次不等式的是( )A、 B、 C、 D、4. 若不等式的解集为 , 则的取值范围是( )A、 B、 C、 D、5. 如果式子 有意义,那么x的取值范围在数轴上表示出来,正确的是( )A、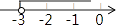 B、
B、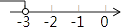 C、
C、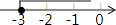 D、
D、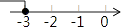 6. 关于 , 的方程组 , 已知 , 则的取值范围为( )A、 B、 C、 D、7. 已知实数 , 同时满足三个条件:① ;② ;③ ,那么实数 的取值范围是( )A、 B、 C、 D、8. 老师设计了接力游戏,用合作的方式完成解一元一次不等式,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成解答.过程如图所示:
6. 关于 , 的方程组 , 已知 , 则的取值范围为( )A、 B、 C、 D、7. 已知实数 , 同时满足三个条件:① ;② ;③ ,那么实数 的取值范围是( )A、 B、 C、 D、8. 老师设计了接力游戏,用合作的方式完成解一元一次不等式,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成解答.过程如图所示:
接力中,自己负责的一步出现错误的是( )
A、只有乙 B、甲和乙 C、乙和丙 D、乙和丁二、填空题
-
9. 不等式的解集为 .10. 用不等式表示:a与2的差大于-1 .11. 不等式的非负整数解有个.12. 若关于的分式方程的解小于 , 则的取值范围是13. 关于x的方程的解是正数,则符合条件的a的所有正整数解之和为 .
三、解答题
-
14. x取哪些整数时,不等式与都成立?15. 解不等式: , 并把它的解集在数轴上表示出来.
四、综合题
-
16. 对于两个数 , 我们定义:①表示这两个数的平均数,例如;
②表示这两个数中更大的数,当时,;当时,;例如: . 根据以上材料,解决下列问题:
(1)、填空: , ;(2)、已知 , 求的取值范围;(3)、已知 , 求和的值.17. 定义:已知平面上两点 , , 称为A,B两点之间的折线距离.例如点与点之间的折线距离为 . 如图,已知平面直角坐标系中点 , .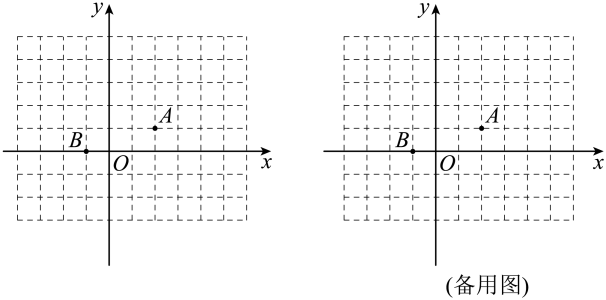 (1)、;(2)、过点B作直线l平行于y轴,求直线l上与点A的折线距离为5的点的坐标;(3)、已知点 , 且 , 求n的取值范围;(4)、已知平面上点P与原点O的折线距离为3,即 , 直接写出所有满足条件的点P围成的图形面积.
(1)、;(2)、过点B作直线l平行于y轴,求直线l上与点A的折线距离为5的点的坐标;(3)、已知点 , 且 , 求n的取值范围;(4)、已知平面上点P与原点O的折线距离为3,即 , 直接写出所有满足条件的点P围成的图形面积.