安徽省合肥市包河区2023-2024学年八年级上学期期中数学试卷

试卷更新日期：2023-12-11 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. 在平面直角坐标系中，点（－1，2）在（）.

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 在函数 $y = \sqrt{x - 1}$ 中，自变量 $x$ 的取值范围是（）

A、 $x \geq 1$ B、 $x \geq - 1$ C、 $x \leq 1$ D、 $x \leq - 1$

查看试题解析
3. 如图，为了估计池塘两岸 $A$ ， $B$ 间的距离，在池塘的一侧选取点 $P$ ，测得 $P A = 15$ 米， $P B = 11$ 米，那么 $A$ ， $B$ 间的距离不可能是（）

A、 $5$ 米 B、 $8.7$ 米 C、 $27$ 米 D、 $18$ 米

查看试题解析
4. 已知一次函数 $y = k x （ k \neq 0 ）$ 经过点 $（ 1 ， 2 ）$ ，则下列不在该函数图象上的点是（）

A、 $（ 0 ， 0 ）$ B、 $（ - 1 ， - 2 ）$ C、 $（ 1 ， - 2 ）$ D、 $（ 3 ， 6 ）$

查看试题解析
5. 在平面直角坐标系中，将线段 $A B$ 平移后得到线段 $A' B'$ ，若点 $A （ - 1 ， 2 ）$ 的对应点 $A'$ 的坐标为 $（ 3 ， - 4 ）$ ，那么点 $B （ 2 ， 4 ）$ 的对应点 $B'$ 的坐标为（）

A、 $（ - 2 ， - 2 ）$ B、 $（ - 2 ， 6 ）$ C、 $（ - 2 ， 10 ）$ D、 $（ 6 ， - 2 ）$

查看试题解析
6. 点 $M （ - 2 ， y_{1} ）$ ， $N （ 3 ， y_{2} ）$ 是函数 $y = - \frac{1}{2} x + b$ 图象上两点，则 $y_{1}$ 与 $y_{2}$ 的大小关系（）

A、 $y_{1} > y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} = y_{2}$ D、无法确定

查看试题解析
7. 如图，BE、CF都是△ABC的角平分线，且∠BDC=130°，则∠A=（）

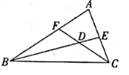A、50° B、60° C、70° D、80°

查看试题解析
8. 在平面直角坐标系 $x O y$ 中，已知点 $A （ - 2 ， 1 ）$ ， $B （ 1 ， 1 ） .$ 若直线 $y = m x$ 与线段 $A B$ 有交点，则 $m$ 的值可以是（）

A、 $- \frac{1}{3}$ B、 $- \frac{2}{3}$ C、 $\frac{1}{3}$ D、 $\frac{2}{3}$

查看试题解析
9. 在物理实验课上，小鹏利用滑轮组及相关器材进行实验，他把得到的拉力 $F （ N ）$ 和所悬挂物体的重力 $G （ N ）$ 的几组数据用电脑绘制成如图象 $（$ 不计绳重和摩擦 $）$ ，请你根据图象判断以下结论正确的序号有（）
$①$ 物体的拉力随着重力的增加而增大； $②$ 当物体的重力 $G = 7 N$ 时，拉力 $F = 2.2 N$ ； $③$ 拉力 $F$ 与重力 $G$ 成正比例函数关系； $④$ 当滑轮组不悬挂物体时，所用拉力为 $0.5 N$ ．

A、 $① ②$ B、 $② ④$ C、 $① ④$ D、 $③ ④$

查看试题解析
10. 在平面直角坐标系中，对于平面内任意一点 $（ x ， y ）$ ，规定以下两种变化： $① f （ x ， y ） = （ - x ， y ）$ ， $② g （ x ， y ） = （ x ， x - y ） .$ 按照该规定： $f （ g （ - 1 ， 2 ）） =$ （）

A、 $（ 1 ， - 3 ）$ B、 $（ 3 ， 1 ）$ C、 $（ 2 ， - 1 ）$ D、 $（ 3 ， - 1 ）$

查看试题解析

二、填空题（本大题共5小题，共15.0分）

11. 在 $△ A B C$ 中， $∠ A = 25 °$ ， $∠ B = 55 °$ ，则 $∠ C =$ $°$ ．

查看试题解析
12. 点 $P （ 3 ， - 2 ）$ 到 $x$ 轴的距离为个单位长度．

查看试题解析
13. 已知直线 $y = - 2 x + 1$ 向下平移 $m （ m > 0 ）$ 个单位后经过点 $（ 1 ， - 3 ）$ ，则 $m$ 的值为．

查看试题解析
14. 如图，AD 是△ABC 的中线，BE 是△ABD 的中线， EF ⊥ BC 于点 F.若 $S_{△ A B C} = 24$ ， BD = 4 ，则 EF 长为.

查看试题解析
15. 已知合肥到芜湖的距离为 $150$ 千米，现有一辆邮政车往返两城市之间，该邮政车每次到达合肥或芜湖后，均需停留 $1$ 小时再重新出发．暑假期间，合肥某旅游公司计划在同线路上加开一辆旅游大巴车，在试运行期间，该邮政车与旅游大巴车同时从合肥出发，两辆车均保持匀速行驶，经过 $\frac{19}{6}$ 小时两车第一次相遇．两车之间的距离 $s$ 千米与行驶时间 $t$ 小时之间的部分函数关系如图所示．已知行驶过程时，邮政车的速度大于旅游大巴车的速度，请完成以下探究：

(1)、邮政车的速度为千米 $/$ 小时；

(2)、当两车第一次在行驶的路上相遇时，相遇点到合肥的距离为千米．

查看试题解析

三、解答题（本大题共8小题，共64.0分。解答应写出文字说明，证明过程或演算步骤）

16. 在平面直角坐标系中，已知点 $A （ a + 1 ， - 3 ）$ ， $B （ 3 ， 2 a + 1 ）$ ．

(1)、若点 $A$ 在 $y$ 轴上，求点 $B$ 的坐标；

(2)、若线段 $A B / / x$ 轴，求 $a$ 的值．

查看试题解析
17. 若 $y$ 与 $x - 3$ 成正比例，且 $x = 5$ 时， $y = - 4$ ，试求出 $y$ 与 $x$ 的函数表达式．

查看试题解析
18. 已知函数 $y = 2 x - 4$ ．

(1)、填表，并画出这个函数的图象：

$x$

$\dots \dots$

$0$
▲

$\dots \dots$

$y = 2 x - 4$

$\dots \dots$
▲

$0$

$\dots \dots$

(2)、根据函数 $y = 2 x - 4$ 的性质或图象，直接写出 $x$ 取何值时， $- 4 \leq y \leq 0$ ．

查看试题解析
19. 在 $△ A B C$ 中， $A B = 8$ ， $B C = 2 a + 2$ ， $A C = 22$ ．

(1)、求 $a$ 的取值范围．

(2)、若 $△ A B C$ 为等腰三角形，求周长．

查看试题解析
20. 已知：如图，△ABC中，AD、AE分别是△ABC的高和角平分线，BF是∠ABC的平分线，BF与AE交于O，若∠ABC＝40°，∠C＝60°，求∠DAE、∠BOE的度数．

查看试题解析
21. 如图，在平面直角坐标系中，一次函数 $y = k x + b$ 的图象经过点 $A （ - 2 ， 6 ）$ ，且与 $x$ 轴相交于点 $B$ ，与正比例函数 $y = 3 x$ 的图象相交于点 $C$ ，点 $C$ 的横坐标为 $1$ ．

(1)、求 $k$ 、 $b$ 的值；

(2)、请直接写出方程组 $\{\begin{array}{l} k x - y = - b \\ 3 x - y = 0 \end{array}$ 的解；

(3)、若点 $D$ 在 $y$ 轴上，且满足 $S_{△ DOC} = S_{△ BOC}$ ，求点 $D$ 的坐标．

查看试题解析
22. 已知甲种水果单价为 $30$ 元 $/$ 千克，若一次性购买甲种水果超过 $40$ 千克，超过部分的价格打八折．某经销商购买甲种水果 $x$ 千克，付款 $y$ 元， $y$ 与 $x$ 之间的函数关系如图所示．

(1)、直接写出图象中 $a$ 的值，并求 $y$ 与 $x$ 之间的函数表达式；

(2)、若乙种水果单价为 $25$ 元 $/$ 千克，该经销商计划一次性购进甲、乙两种水果共 $80$ 千克，且甲种水果不少于 $30$ 千克，但又不超过 $50$ 千克．如何分配甲、乙两种水果的购买量，才能使经销商付款总金额 $w （$ 元 $）$ 最少？最少付款金额是多少？

查看试题解析
23. 若关于自变量 $x$ 的函数 $y = | 2 x - 3 | - 2 a$ 的函数值始终大于 $y = | x + a |$ 的函数值，则求 $a$ 的取值范围．

查看试题解析

$x$	$\dots \dots$	$0$	▲	$\dots \dots$
$y = 2 x - 4$	$\dots \dots$	▲	$0$	$\dots \dots$