山东省济南市市中区2023-2024学年八年级上学期期中考试数学试卷
试卷更新日期:2023-12-11 类型:期中考试
一、选择题(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,
-
1. 实数4的平方根是( )A、2 B、-2 C、 D、±22. 如图,在平面直角坐标系xOy中,被一团墨水覆盖住的点的坐标有可能是( )
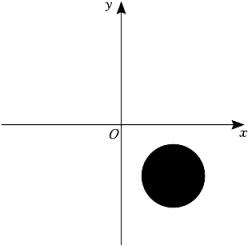 A、(2,-4) B、(-2,4) C、(-2,-4) D、(2,4)3. 在△ABC中a , b , c分别是∠A、∠B , ∠C的对边,下列条件中,不能判断△ABC是直角三角形的是( )A、a:b:c=5:12:13 B、 C、∠A:∠B:∠C=3:4:5 D、∠A+∠B=∠C4. 下列数中-4, , 3.1415,-3π,3.030030003…中,无理数的个数是( )A、1 B、2 C、3 D、45. 下列计算中,结果错误的是( )A、 B、 C、 D、6. 已知点(-2,y1),(3,y2)都在直线y=-x+1上,则y1与y2的大小关系是( )A、y1<y2 B、y1=y2 C、y1>y2 D、无法确定7. 一次函数y1=ax+b与正比例函数y2=-bx在同一坐标系中的图象大致是( )A、
A、(2,-4) B、(-2,4) C、(-2,-4) D、(2,4)3. 在△ABC中a , b , c分别是∠A、∠B , ∠C的对边,下列条件中,不能判断△ABC是直角三角形的是( )A、a:b:c=5:12:13 B、 C、∠A:∠B:∠C=3:4:5 D、∠A+∠B=∠C4. 下列数中-4, , 3.1415,-3π,3.030030003…中,无理数的个数是( )A、1 B、2 C、3 D、45. 下列计算中,结果错误的是( )A、 B、 C、 D、6. 已知点(-2,y1),(3,y2)都在直线y=-x+1上,则y1与y2的大小关系是( )A、y1<y2 B、y1=y2 C、y1>y2 D、无法确定7. 一次函数y1=ax+b与正比例函数y2=-bx在同一坐标系中的图象大致是( )A、 B、
B、 C、
C、 D、
D、 8. 如图一个三级台阶,它的每一级的长宽高分别是5cm , 3cm和1cm , A和B是这个台阶的两个相对的端点,点A上有一只蚂蚁,想到点B去吃可口的食物,则蚂蚁沿着台阶面爬到点B的最短路程长为( )
8. 如图一个三级台阶,它的每一级的长宽高分别是5cm , 3cm和1cm , A和B是这个台阶的两个相对的端点,点A上有一只蚂蚁,想到点B去吃可口的食物,则蚂蚁沿着台阶面爬到点B的最短路程长为( ) A、10 B、11 C、12 D、139. 在物理实验课上,小鹏利用滑轮组及相关器材进行实验,他把得到的拉力F(N)和所悬挂物体的重力G(N)的几组数据用电脑绘制成如图象(不计绳重和摩擦),请你根据图象判断以下结论正确的序号有( )
A、10 B、11 C、12 D、139. 在物理实验课上,小鹏利用滑轮组及相关器材进行实验,他把得到的拉力F(N)和所悬挂物体的重力G(N)的几组数据用电脑绘制成如图象(不计绳重和摩擦),请你根据图象判断以下结论正确的序号有( )
①物体的拉力随着重力的增加而增大;
②当物体的重力G=7N时,拉力F=2.2N;
③拉力F与重力G成正比例函数关系;
④当滑轮组不悬挂物体时,所用拉力为0.5N .
A、①② B、②④ C、①④ D、③④10. 如图,在平面直角坐标系中,长为2的线段AB(点B在点A上面)在y轴上移动,C(1,0),D(4,0),连接AC , BD , 则AC+BD的最小值为( )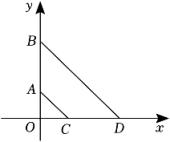 A、5 B、 C、2 D、
A、5 B、 C、2 D、二、填空题(共6小题,每小题4分,满分24分.填空题请直接填写答案.)
-
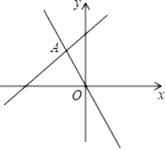
11. 若(1,2)表示教室里第1列第2排的位置,则教室里第4列第3排的位置可以表示为 .12. 已知点P(2-a , a-3)在y轴上,则a= .13. 如图,一次函数y=-2x和y=kx+b的图象相交于点A(-2,4),则关于x的方程kx+b+2x=0的解是 .
 14. 小明是一个电脑爱好者,他设计了一个程序,如图.当输入x的值是64时,输出的y值是.
14. 小明是一个电脑爱好者,他设计了一个程序,如图.当输入x的值是64时,输出的y值是. 15. 甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与行驶时间x(小时)之间的函数关系如图所示,已知甲对应的函数关系式为y=60x , 根据图象提供的信息可知从乙出发后追上甲车需要 小时.
15. 甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与行驶时间x(小时)之间的函数关系如图所示,已知甲对应的函数关系式为y=60x , 根据图象提供的信息可知从乙出发后追上甲车需要 小时. 16. 如图所示,是由北京国际数学家大会的会徽演化而成的图案,其主体部分是由一连串的等腰直角三角形依次连接而成,其中∠MA1A2=∠MA2A3⋯=∠MAnAn+1=90°,(n为正整数),若M点的坐标是(-1,2),A1的坐标是(0,2),则A2023的坐标为 .
16. 如图所示,是由北京国际数学家大会的会徽演化而成的图案,其主体部分是由一连串的等腰直角三角形依次连接而成,其中∠MA1A2=∠MA2A3⋯=∠MAnAn+1=90°,(n为正整数),若M点的坐标是(-1,2),A1的坐标是(0,2),则A2023的坐标为 .
三、解答题(本大题共10个小题,共86分.解答应写出文字说明、证明过程或演算步
-
17. 计算:(1)、;(2)、 .18. 解方程:(1)、(x-4)2-9=0;(2)、(x+1)3=-27.19. 学过《勾股定理》后,李老师和“几何小分队”的队员们到操场上测量旗杆AB高度,得到如下信息:

①测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长2米(如图1);
②当将绳子拉直时,测得此时拉绳子的手到地面的距离CD为1米,到旗杆的距离CE为9米(如图2).
根据以上信息,求旗杆AB的高度.
20. 在平面直角坐标系中,△ABC的位置如图所示,已知点A的坐标是(-4,3). (1)、点B的坐标为( , ),点C的坐标为( , ).(2)、△ABC的面积是 .(3)、作点C关于y轴的对称点C',那么A、C'两点之间的距离是 ▲ .21. 如图,学校准备在阴影部分修建草坪,经施工人员测量,∠ADC=90°,AD=8米,CD=6米,AB=26米,BC=24米.
(1)、点B的坐标为( , ),点C的坐标为( , ).(2)、△ABC的面积是 .(3)、作点C关于y轴的对称点C',那么A、C'两点之间的距离是 ▲ .21. 如图,学校准备在阴影部分修建草坪,经施工人员测量,∠ADC=90°,AD=8米,CD=6米,AB=26米,BC=24米. (1)、判断△ABC的形状并证明.(2)、求草坪(阴影部分)的面积.22. 一次函数y=kx+b的图象与x轴交于点A , 与y轴交于点B(0,2).已知点C(-1,3)在该图象上,连接OC .
(1)、判断△ABC的形状并证明.(2)、求草坪(阴影部分)的面积.22. 一次函数y=kx+b的图象与x轴交于点A , 与y轴交于点B(0,2).已知点C(-1,3)在该图象上,连接OC . (1)、求函数y=kx+b的关系式;(2)、求△AOB的面积;(3)、点P为x轴上一动点,若S△ACP=3S△AOB , 求点P的坐标.23. 某校八年级开展了《为家人选择合适的手机套餐》项目学习.小露收集并整理奶奶近六个月的话费账单,根据她的月平均通话时间筛选出两款比较适合她的手机套餐.甲套餐:月租费8元,送30分钟通话时间,超出的部分按每分钟0.25元计;乙套餐:月租费29元,通话费按每分钟0.1元计.
(1)、求函数y=kx+b的关系式;(2)、求△AOB的面积;(3)、点P为x轴上一动点,若S△ACP=3S△AOB , 求点P的坐标.23. 某校八年级开展了《为家人选择合适的手机套餐》项目学习.小露收集并整理奶奶近六个月的话费账单,根据她的月平均通话时间筛选出两款比较适合她的手机套餐.甲套餐:月租费8元,送30分钟通话时间,超出的部分按每分钟0.25元计;乙套餐:月租费29元,通话费按每分钟0.1元计. (1)、每月的手机资费y(元)与通话时间x(分)之间存在函数关系,y与x之间的关系式为:y甲= , y乙=(x≥0).(填写最简结果)(2)、为了直观比较,在同一坐标系内画出两个函数的图象(如图).
(1)、每月的手机资费y(元)与通话时间x(分)之间存在函数关系,y与x之间的关系式为:y甲= , y乙=(x≥0).(填写最简结果)(2)、为了直观比较,在同一坐标系内画出两个函数的图象(如图).①写出图中A点表示的实际意义.
②如果从节省费用的角度考虑,应如何选择套餐?
24. 小明在解决问题:已知 , 求2a2-8a+1的值.他是这样分析与解的:∵
∴ , ∴(a-2)2=3,a2-4a+4=3
∴a2-4a=-1,∴2a2-8a+1=2(a2-4a)+1=2×(-1)+1=-1.
请你根据小明的分析过程,解决如下问题:
(1)、= , = .(2)、化简: .(3)、若 , 请按照小明的方法求出4a2-8a+1的值.25. 如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA , 过点A作AD⊥I交于点D , 过点B作BE⊥l交于点E , 易得△ADC≌△CEB , 我们称这种全等模型为“k型全等”.如图2,在直角坐标系中,直线l1:y=kx+2分别与y轴,x轴交于点A、B(-1,0). (1)、求k的值和点A的坐标;(2)、在第二象限构造等腰直角△ABE , 使得∠BAE=90°,求点E的坐标;(3)、将直线l1绕点A旋转45°得到l2 , 求l2的函数表达式.26. △ABC中,AC=BC , ∠ACB=90°,D为△ABC外一点.
(1)、求k的值和点A的坐标;(2)、在第二象限构造等腰直角△ABE , 使得∠BAE=90°,求点E的坐标;(3)、将直线l1绕点A旋转45°得到l2 , 求l2的函数表达式.26. △ABC中,AC=BC , ∠ACB=90°,D为△ABC外一点. (1)、【探究发现】如图1,点D在边AB下方,∠ADB=90°.学校的数学兴趣小组的同学们尝试探究此时线段AD、BD、CD之间的数量关系.他们的思路是这样的,作EC⊥CD , 取EC=CD , 连接BE . 易证△ADC≌△BEC . 通过等量代换得到线段之间的数量关系.请根据同学们的思路,写出△ADC≌△BEC的证明过程.(2)、【迁移运用】如图2,点D在边AB上方,∠ADB=90°.猜想线段AD、BD、CD之间的数量关系,并证明你的结论.(3)、【延伸拓展】如图3,在四边形ABCD中,∠ABC=∠BAC=∠ADC=45°,若AD=2,CD=4,请直接写出BD的值.
(1)、【探究发现】如图1,点D在边AB下方,∠ADB=90°.学校的数学兴趣小组的同学们尝试探究此时线段AD、BD、CD之间的数量关系.他们的思路是这样的,作EC⊥CD , 取EC=CD , 连接BE . 易证△ADC≌△BEC . 通过等量代换得到线段之间的数量关系.请根据同学们的思路,写出△ADC≌△BEC的证明过程.(2)、【迁移运用】如图2,点D在边AB上方,∠ADB=90°.猜想线段AD、BD、CD之间的数量关系,并证明你的结论.(3)、【延伸拓展】如图3,在四边形ABCD中,∠ABC=∠BAC=∠ADC=45°,若AD=2,CD=4,请直接写出BD的值.