2023-2024学年初中数学八年级上册 3.3 实数同步分层训练培优卷(湘教版)

试卷更新日期：2023-12-11 类型：同步测试

进入出卷网下载

一、选择题

1. 下列说法正确的是（）

A、实数分为正实数和负实数 B、无限小数都是无理数 C、带根号的数都是无理数 D、无理数都是无限不循环小数

查看试题解析
2. 如图，若数轴上点A、B对应的实数分别为.− $\sqrt{2}$ 和 $\sqrt{2}$ ，以B为圆心，BA长为半径画弧与正半轴交点C，则点C对应的实数是（）

A、 $\sqrt{2}$ B、2 $\sqrt{2}$ C、 $3 \sqrt{2}$ D、 $4 \sqrt{2}$

查看试题解析
3. 在实数 $0 ， - 2 ， - \sqrt{6} ， - 3$ 中，最小的是（）

A、0 B、 $- 2$ C、 $- \sqrt{6}$ D、-3

查看试题解析
4. 为了证明数轴上的点可以表示无理数，老师给学生设计了如下材料：如图，直径为1个单位长度的圆从原点沿数轴向右滚动一周，圆上一点由原点（记为点O）到达点A，点A对应的数是（）

A、 $π$ B、3.14 C、 $ - π$ D、－3.14

查看试题解析
5. 估算 $\sqrt{13} - 3$ 的值，下列结论正确的是（）

A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间

查看试题解析
6. 如图，数轴上的点E，F，G，M，N，P分别表示数 $- 1$ ， 0，1，2，3，4，则表示数 $\sqrt{17} - 3$ 的点应落在（　　）

A、线段 $E F$ 上 B、线段 $G M$ 上 C、线段 $M N$ 上 D、线段 $N P$ 上

查看试题解析
7. 求 $| \frac{1}{2} x - 1 | + | \frac{1}{3} x - 2 | + | \frac{1}{4} x - 3 |$ 的最小值（　　）

A、12 B、6 C、 $\frac{7}{2}$ D、3

查看试题解析
8. 自定义运算： $a ☆ b = {\begin{array}{l} a - 2 b (a < b) \\ 2 a - b (a \geq b) \end{array}$ 例如： $2 ☆ (- 4) = 2 \times 2 - (- 4) = 8$ ，若m，n在数轴上的位置如图所示，且 $(m + n) ☆ (m - n) = 7$ ，则 $6 n - 2 m + 2021$ 的值等于（）

A、2028 B、2035 C、2028或2035 D、2021或2014

查看试题解析

二、填空题

9. 如图，把半径为1的圆从数轴上表示-1的点A开始沿数轴向右滚动一周，圆上的点A到达点 $A^{'}$ ，则点 $A^{'}$ 表示的数为．

查看试题解析
10. 若 $m$ 是 $\sqrt{6}$ 的小数部分，则 $m^{2} =$ ．

查看试题解析
11. 已知 $4 3^{2} = 1849$ ， $4 4^{2} = 1936$ ， $4 5^{2} = 2025$ ， $4 6^{2} = 2116$ ．若n为整数且 $n < \sqrt{2023} < n + 1$ ，则n的值为．

查看试题解析

12. 如图，将 1、

\sqrt{2} ， \sqrt{3}

，三个数按图中方式排列，若规定（a，b）表示第

a

排第

b

列的数，（3，2）为第 3 排第 2 列的数为

\sqrt{2}

，则（8，2）与（100，100）表示的两个数的积是．

					1	第一排
				$\sqrt{3}$	$\sqrt{2}$	第二排
			$\sqrt{3}$	$\sqrt{2}$	$1$	第三排
		$1$	$\sqrt{3}$	$\sqrt{2}$	$1$	第四排
	$\sqrt{3}$	$\sqrt{2}$	$1$	$\sqrt{3}$	$\sqrt{2}$	第五排
……	第五列	第四列	第三列	第二列	第一列	……

查看试题解析

13. 若 $x + y + z = 0$ ，且x，y，z均不为零，则 $\frac{x}{| x |} + \frac{| y |}{y} + \frac{z}{| z |}$ 的值为．

查看试题解析

三、解答题

14. 已知 $2 a - 1$ 的平方根是 $\pm 3$ ， $3 a + b - 9$ 的立方根是2，c是 $- \sqrt{57}$ 的整数部分，求 $a + 2 b + c$ 的算术平方根．

查看试题解析
15. 先阅读然后解答提出的问题：
设a、b是有理数，且满足 $a + \sqrt{2} b = 3 - 2 \sqrt{2}$ ，求b^a的值．
解：由题意得 $(a - 3) + (b + 2) \sqrt{2} = 0$ ，
因为a、b都是有理数，所以a-3，b+2也是有理数，
由于 $\sqrt{2}$ 是无理数，所以a-3=0，b+2=0，
所以a=3，b=-2，所以 $b^{a} = (- 2)^{3} = - 8$ ．
问题：设x、y都是有理数，且满足 $x^{2} - 2 y + \sqrt{5} y = 10 + 3 \sqrt{5}$ ，求x+y的值．

查看试题解析

四、综合题

16. 下面是小李同学探索 $\sqrt{107}$ 的近似数的过程：
∵面积为107的正方形边长是 $\sqrt{107}$ ，且 $10 ＜ \sqrt{107} ＜ 11$ ，
∴设 $\sqrt{107} = 10 + x$ ，其中0＜x＜1，画出如图示意图，
∵图中S_正方形＝10²+2×10•x+x² ， S_正方形＝107
∴10²+2×10•x+x²＝107
当x²较小时，省略x² ，得20x+100≈107，得到x≈0.35，即 $\sqrt{107} \approx 10.35$ ．

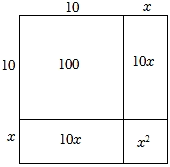(1)、 $\sqrt{76}$ 的整数部分是；

(2)、仿照上述方法，探究 $\sqrt{76}$ 的近似值．（画出示意图，标明数据，并写出求解过程）

查看试题解析
17. 我们容易发现： $2^{2} + 3^{2} > 2 \times 2 \times 3$ ； $5^{2} + 5^{2} = 2 \times 5 \times 5$ ； $5^{2} + 3^{2} > 2 \times 5 \times 3$ ．

(1)、观察以上各式，请判断 $a^{2} + b^{2}$ 与 $2 a b$ 之间的大小关系，并说明理由；

(2)、利用（1）中的结论，当 $a > 0$ ， $b > 0$ 时，求 $\frac{b}{a} + \frac{a}{b}$ 的最小值；

(3)、根据（1）中的结论猜想 ${(\frac{a + b}{2})}^{2}$ 与 $a b$ 之间的大小关系，并说明理由．

查看试题解析

2023-2024学年初中数学八年级上册 3.3 实数 同步分层训练培优卷(湘教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学八年级上册 3.3 实数同步分层训练培优卷(湘教版)