2023-2024学年初中数学八年级上册 3.2 立方根同步分层训练培优卷(湘教版)

试卷更新日期：2023-12-11 类型：同步测试

进入出卷网下载

一、选择题

1. 实数a的立方根与 $\sqrt{4}$ 的倒数相等，则a的值为（）

A、8 B、 $- 8$ C、 $\frac{1}{8}$ D、 $- \frac{1}{8}$

查看试题解析
2. 下列说法正确的有（）
①带根号的数都是无理数；
②立方根等于本身的数是0和1；
③－a一定没有平方根；
④实数与数轴上的点是一一对应的；
⑤两个无理数的差还是无理数

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列运算中，正确的是（）

A、 $\sqrt{9}$ $= \pm 3$ B、 $\sqrt{|- 4|} = 2$ C、 $\sqrt[3]{- 8}$ $= 2$ D、 $\sqrt{(- 8)^{2}} = - 8$

查看试题解析
4. 下列说法中，错误的是（）

A、4的算术平方根是±2 B、 $\sqrt{81}$ 的平方根是±3 C、8的立方根是2 D、立方根等于－1的实数是－1

查看试题解析
5. 下列命题是真命题的是（）

A、过一点有且只有一条直线和已知直线平行 B、 $\sqrt{a^{2}} = \sqrt{b^{2}}$ ，则 $a = b$ C、 $a$ 与 $b$ 互为相反数，则 $\sqrt[3]{b}$ 与 $\sqrt[3]{a}$ 互为相反数 D、 $\sqrt[3]{64}$ 的平方根是2

查看试题解析
6. 已知甲、乙两个立方体，甲的体积是乙体积的8倍，则甲的棱长是乙的棱长的（）

A、8倍 B、2倍 C、4倍 D、 $\frac{1}{2}$ 倍

查看试题解析
7. 若某自然数的立方根为 $a$ ，则它前面与其相邻的自然数的立方根是（）

A、 $a - 1$ B、 $\sqrt[3]{a - 1}$ C、 $\sqrt[3]{a^{3} - 1}$ D、 $a^{3} - 1$

查看试题解析
8. 已知， $\sqrt[3]{x - 1} = x - 1$ ，则x²-x的值为（）

A、0 或 1 B、0 或 2 C、0 或 6 D、0、2 或 6

查看试题解析

二、填空题

9. 已知 $x^{3} = 8$ ， $| y | = 9$ ， $x y < 0$ ，那么 $x^{2} - y =$ ．

查看试题解析
10. 已知 $\sqrt[3]{1.12}$ ≈1.038， $\sqrt[3]{11.2}$ ≈2.237， $\sqrt[3]{112}$ ≈4.820，则 $\sqrt[3]{- 11200}$ ≈ ．

查看试题解析
11. 数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：求59319的立方根．华罗庚脱口而出：39．众人感觉十分惊奇，请华罗庚给大家解读其中的奥秘．
你知道怎样迅速准确的计算出结果吗？请你按下面的问题试一试：

① 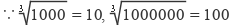，又，

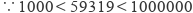，∴能确定59319的立方根是个两位数．

②∵59319的个位数是9，又，∴能确定59319的立方根的个位数是9．

③如果划去59319后面的三位319得到数59，

而，则，可得，

由此能确定59319的立方根的十位数是3

因此59319的立方根是39．

(1)、现在换一个数195112，按这种方法求立方根，请完成下列填空．
①它的立方根是位数．

②它的立方根的个位数是．

③它的立方根的十位数是．

④195112的立方根是．

(2)、请直接填写结果：
① ．

② ．

查看试题解析
12. 我国数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：求59319的立方根，华罗庚脱口说出答案，众人十分惊奇，忙问计算的奥妙．你知道他是怎样迅速准确地计算出结果的吗？
下面是小超的探究过程，请补充完整：

(1)、求 $\sqrt[3]{59319}$ ；
①由10³＝1000，100³＝1 000 000，可以确定 $\sqrt[3]{59319}$ 是位数；

②由59319的个位上的数是9，可以确定 $\sqrt[3]{59319}$ 的个位上的数是；

③如果划去59319后面的三位319得到数59，而3³＝27，4³＝64，可以确定 $\sqrt[3]{59319}$ 的十位上的数是；

由此求得 $\sqrt[3]{59319}$ ＝．

(2)、已知103823也是一个整数的立方，用类似的方法可以求得 $\sqrt[3]{103823}$ ＝．

查看试题解析
13. 1，2，3……，100这100个自然数的算术平方根和立方根中，无理数的个数有个。

查看试题解析

三、解答题

14. 已知 $2 x + y + 17$ 的立方根是3，16的算术平方根是 $2 x - y + 2$ ，求： $x^{2} + y^{2}$ 的平方根．

查看试题解析
15. 已知2a﹣1的平方根是±3，3a+b+9的立方根是3，求2（a+b）的平方根．

查看试题解析

四、综合题

16. 观察发现：

a

…

0.0 001

0.01

1

100

10 000

…

$\sqrt{a}$

…

0.01

x

1

y

100

…

(1)、表格中x= ， y=.

(2)、应用：利用a与 $\sqrt{a}$ 数位的规律解决下面两个问题：
①已知 $\sqrt{10}$ ≈ 3.16，则 $\sqrt{1 000}$ ≈ ， $\sqrt{0.1}$ ≈；

②已知 $\sqrt{2 021}$ = k， $\sqrt{20.21}$ = ， $\sqrt{202 100}$ =（用含k的式子表示）.

(3)、拓展： $\sqrt[3]{2 020}$ = m， $\sqrt[3]{2.02}$ = ， $\sqrt[3]{2 020 000}$ =（用含m的式子表示）

查看试题解析
17. 据说我国著名数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：一个数是59319，希望求出它的立方根．华罗庚脱口而出：39．邻座的乘客十分惊奇，忙问计算的奥妙，华罗庚讲述了计算过程：
第一步：因为 $1 0^{3} = 1000$ ， $10 0^{3} = 1000000$ ， $1000 < 59319 < 1000000$ ，所以 $10 < \sqrt[3]{59319} < 100$ ．
第二步：因为59319的个位上的数是9，只有个位数字是9的数的立方的个位数字是9，所以 $\sqrt[3]{59319}$ 的个位数字是9．
第三步：如果划去59319后面的三位319得到数59，而 $3^{3} = 27$ ， $4^{3} = 64$ ，所以 $30 < \sqrt[3]{59000} < 40$ ，
所以 $30 < \sqrt[3]{59319} < 40$ ，即 $\sqrt[3]{59319}$ 的十位数字是3．
所以 $\sqrt[3]{59319} = 39$ ．
请根据上述材料解答下列问题：

(1)、用上述方法确定4913的立方根的个位数字是．

(2)、用上述方法确定50653的立方根是．

(3)、求 $\sqrt[3]{110592}$ 的值，要求写出计算过程．

查看试题解析

a	…	0.0 001	0.01	1	100	10 000	…
$\sqrt{a}$	…	0.01	x	1	y	100	…

2023-2024学年初中数学八年级上册 3.2 立方根 同步分层训练培优卷(湘教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学八年级上册 3.2 立方根同步分层训练培优卷(湘教版)