2023-2024学年初中数学八年级上册 2.6 用尺规作三角形 同步分层训练培优卷(湘教版)
试卷更新日期:2023-12-11 类型:同步测试
一、选择题
-
1. 如图,用直尺和圆规作图,以点O为圆心,适当长为半径画弧,分别交OB , OA于点E、D , 再分别以点E、D为圆心,大于ED的长为半径画弧,两弧交于点C , 连接OC , 则△ODC≌OEC的理由是( )
 A、SSS B、SAS C、AAS D、ASA2. 在以下图形中,根据尺规作图痕迹,不能判断射线AD平分∠BAC的是( )
A、SSS B、SAS C、AAS D、ASA2. 在以下图形中,根据尺规作图痕迹,不能判断射线AD平分∠BAC的是( ) A、① B、② C、③ D、④3. 如图,在中, , 以点B为圆心,适当长为半径画弧,交于点M,交于点N,分别以点M、N为圆心,大于的长为半径画弧,两弧在的内部相交于点P,画射线 , 交于点D,若 , 则的度数是( )
A、① B、② C、③ D、④3. 如图,在中, , 以点B为圆心,适当长为半径画弧,交于点M,交于点N,分别以点M、N为圆心,大于的长为半径画弧,两弧在的内部相交于点P,画射线 , 交于点D,若 , 则的度数是( )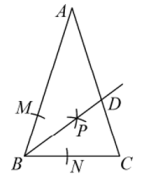 A、 B、 C、 D、4. 如图,在△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
A、 B、 C、 D、4. 如图,在△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:(甲)作AB的中垂线,交BC于P点,则P即为所求;
(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求.
对于两人的作法,下列判断何者正确?( )
 A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确5. 如图,是的外接圆,在弧上找一点 , 使点平分弧 . 以下是嘉嘉和琪琪两位同学提供的两种不同的作法:
A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确5. 如图,是的外接圆,在弧上找一点 , 使点平分弧 . 以下是嘉嘉和琪琪两位同学提供的两种不同的作法:嘉嘉:如图1,作的平分线 , 交弧于点 , 则点即为所求.
琪琪:如图2,作的垂直平分线 , 交弧于点 , 则点即为所求.

对于上面的两种作图方法,下面的说法正确的是( )
A、嘉嘉的作法正确 B、琪琪的作法正确 C、嘉嘉和琪琪的作法都错误 D、嘉嘉和琪琪的作法都正确6. 如图,点C在∠AOB的OB边上,用尺规作出了∠BCD=∠AOB.以下是排乱的作图过程:①以点C为圆心,OE长为半径画 , 交OB于点M.②作射线CD,则∠BCD=∠AOB.③以点M为圆心,EF长为半径画弧,交于点D.④以点O为圆心,任意长为半径画 , 分别交OA,OB于点E,E则正确的作图顺序是( )
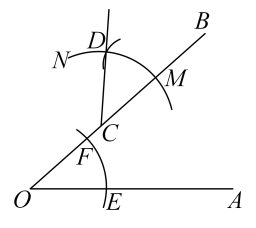 A、①②③④ B、③②④① C、④①③② D、④③①②7. 在△ABC中,D是AC上一点,利用尺规在AB上作出一点E,使得 , 则符合要求的作图痕迹是( )A、
A、①②③④ B、③②④① C、④①③② D、④③①②7. 在△ABC中,D是AC上一点,利用尺规在AB上作出一点E,使得 , 则符合要求的作图痕迹是( )A、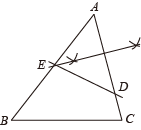 B、
B、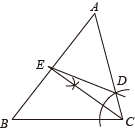 C、
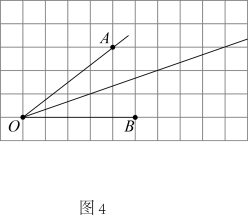
C、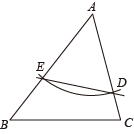 D、
D、
二、填空题
-
8. 如图,在中, , 以点A为圆心,任意长为半径画弧,分别交AB、AC于点M、N,再分别以点M、N为圆心,大于的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,若 , 则的度数是 .
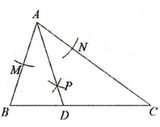 9. 已知:∠AOB,求作:∠AOB的平分线.作法:①以点O为圆心,适当长为半径画弧,分别交OA,OB于点M,N;②分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在∠AOB内部交于点C;③画射线OC.射线OC即为所求.上述作图用到了全等三角形的判定方法,这个方法是.
9. 已知:∠AOB,求作:∠AOB的平分线.作法:①以点O为圆心,适当长为半径画弧,分别交OA,OB于点M,N;②分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在∠AOB内部交于点C;③画射线OC.射线OC即为所求.上述作图用到了全等三角形的判定方法,这个方法是. 10. 如图,在 中, , ,以A为圆心,任意长为半径画弧分别交 、 于点M和N,再分别以M,N为圆心,大于 的长为半径画弧,两弧交于点P,连结 并延长交 于点D,则下列说法中正确有.(填序号)
10. 如图,在 中, , ,以A为圆心,任意长为半径画弧分别交 、 于点M和N,再分别以M,N为圆心,大于 的长为半径画弧,两弧交于点P,连结 并延长交 于点D,则下列说法中正确有.(填序号)
①作出 的依据是 ;
② ;
③点D在 的中垂线上;
④ .
11. 如图,在长方形网格中,每个小长方形的长为 ,宽为 , , 两点在网格格点上,若点 也在网格格点上,以 , , 为顶点的三角形的面积为 ,则满足条件的点 有个.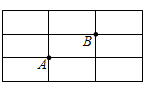 12. 如图,平面内有五个点,以其中任意三个点为顶点画三角形,最多可以画个三角形.
12. 如图,平面内有五个点,以其中任意三个点为顶点画三角形,最多可以画个三角形.
三、解答题
-
13. 已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形.(尺规作图,保留作图痕迹,不写作法)
 14. 如图,已知∠AOB及点E、F,在∠AOB的内部求作点P,使点P到OA、OB的距离相等,且PE=PF.(请尺规作图,保留作图痕迹,并写结论)
14. 如图,已知∠AOB及点E、F,在∠AOB的内部求作点P,使点P到OA、OB的距离相等,且PE=PF.(请尺规作图,保留作图痕迹,并写结论)
四、作图题
-
15. 图①、图②、图③均是由小正方形组成的的网格,的三个顶点A、B、C均在格点(网格线的交点)上,请按要求在给定的网格中,仅用无刻度的直尺,分别按下列要求作图,保留作图痕迹,不写画法.
 (1)、在图①中的上确定一点D , 连结 , 使 .(2)、在图②中的上确定一点E , 连结 , 使 .(3)、在图③中的上确定一点F , 连结 , 使 .16. 如图,中,用尺规作图法在上做一点 , 使得 . (保留作图痕迹,不用写作法)
(1)、在图①中的上确定一点D , 连结 , 使 .(2)、在图②中的上确定一点E , 连结 , 使 .(3)、在图③中的上确定一点F , 连结 , 使 .16. 如图,中,用尺规作图法在上做一点 , 使得 . (保留作图痕迹,不用写作法)
五、综合题
-
17. 如图
 (1)、尺规作图1:
(1)、尺规作图1:已知:如图,线段AB和直线且点B在直线上
求作:点C,使点C在直线上并且使△ABC为等腰三角形.
作图要求:保留作图痕迹,不写作法,做出所有符合条件的点C.
(2)、特例思考:如图一,当∠1=90°时,符合(1)中条件的点C有个;如图二,当∠1=60°时,符合(1)中条件的点C有个.
(3)、拓展应用:如图,∠AOB=45°,点M,N在射线OA上,OM=x,ON=x+2,点P是射线OB上的点.若使点P,M,N构成等腰三角形的点P有且只有三个,求x的值.
18. 如图,在四边形ABCD中,∠B=∠C= 90°,AB>CD,AD=AB+CD. (1)、利用尺规作∠ADC的平分线DE,交BC于点E,连接AE. (保留作图痕迹,不写作法)(2)、在(1)的条件下,求证:AE⊥DE.19. 阅读下列材料,并完成相应的学习任务:
(1)、利用尺规作∠ADC的平分线DE,交BC于点E,连接AE. (保留作图痕迹,不写作法)(2)、在(1)的条件下,求证:AE⊥DE.19. 阅读下列材料,并完成相应的学习任务:一次有意义的动手实践活动——在格点图中巧作角平分线
实践背景
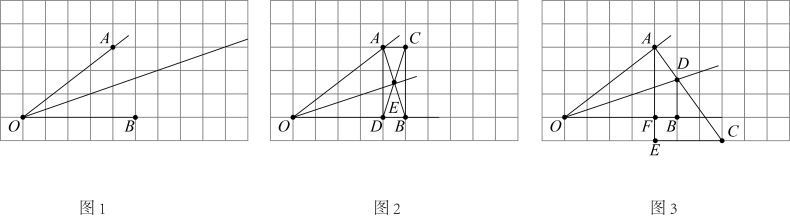
在一次动手实践课上,老师提出如下问题:在如图1所示由边长为1的小正方形组成的格点图中,点 , , 都在小正方形的顶点处,仅用无刻度的直尺作出的角平分线.
成果展示
小明、小亮展示了如下作法:
小明:如图2,在格点图中取格点 , . 连接 , 交于点 . 作出射线 .
∵四边形是矩形,∴(依据1).
∵ , ∴平分 .
小亮:如图3,在格点图中取格点 . 连接 , 与小正方形的边交于点 . 则 .
∵ , .
∴(依据2).
∴ , 即平分 .
学习任务:
(1)、实践反思:①请填写出上述材料中的依据1和依据2.
依据1: ▲ ;依据2: ▲ .
②请根据小亮的作法,证明 .
(2)、创新再探请你根据实践背景问题要求,采用不同于小明和小亮的作法,描出作图过程中的所取得的点,作出的角平分线(不写作法,不需要说明理由).