2023-2024学年初中数学八年级上册 2.6 用尺规作三角形 同步分层训练基础卷(湘教版)
试卷更新日期:2023-12-11 类型:同步测试
一、选择题
-
1. 如图, , 以点为圆心,小于的长为半径作圆弧,分别交 , 于 , 两点,再分别以 , 为圆心,以大于长为半径作圆弧两条弧交于点 , 作射线交于点 , 若 , 则( )
 A、 B、 C、 D、2. 观察下列尺规作图的痕迹:
A、 B、 C、 D、2. 观察下列尺规作图的痕迹:
其中,能够说明的是( )
A、①② B、②③ C、①③ D、③④3. 用直尺和圆规作一个角等于已知角的示意图如下,则要说明 , 需要证明和 , 则这两个三角形全等的依据是( ) A、 B、 C、 D、4. 观察下列尺规作图的痕迹,不能判断是等腰三角形的是( ).A、
A、 B、 C、 D、4. 观察下列尺规作图的痕迹,不能判断是等腰三角形的是( ).A、 B、
B、 C、
C、 D、
D、 5. 如图,已知 , 求作 , 使得.根据尺规作图的痕迹,下列结论不一定正确的是( )
5. 如图,已知 , 求作 , 使得.根据尺规作图的痕迹,下列结论不一定正确的是( ) A、圆弧与圆弧是等弧 B、线段与线段的长相等 C、圆弧与圆弧的半径相等 D、扇形与扇形的面积相等6. 如图所示,以 的顶点 O 为圆心,适当长为半径画弧,交 于点 C,交 于点 D,再分别以点 C 、 D 为圆心,大于 长为半径画弧,两弧在 内部交于点 E,过点 E 作射线 , 连接则下列说法错误的( )
A、圆弧与圆弧是等弧 B、线段与线段的长相等 C、圆弧与圆弧的半径相等 D、扇形与扇形的面积相等6. 如图所示,以 的顶点 O 为圆心,适当长为半径画弧,交 于点 C,交 于点 D,再分别以点 C 、 D 为圆心,大于 长为半径画弧,两弧在 内部交于点 E,过点 E 作射线 , 连接则下列说法错误的( ) A、射线 是 的平分线 B、 是等腰三角形 C、C、D 两点关于 所在直线对称 D、O、E 两点关于 所在直线对称7. 数学课上,老师提出一个问题:经过已知角一边上的点,做一个角等于已知角.如图,用尺规过的边上一点C(图①)作(图②).我们可以通过以下步骤作图:
A、射线 是 的平分线 B、 是等腰三角形 C、C、D 两点关于 所在直线对称 D、O、E 两点关于 所在直线对称7. 数学课上,老师提出一个问题:经过已知角一边上的点,做一个角等于已知角.如图,用尺规过的边上一点C(图①)作(图②).我们可以通过以下步骤作图:①作射线;②以点O为圆心,小于的长为半径作弧,分别交 , 于点N,M;③以点P为圆心,的长为半径作弧,交上一段弧于点Q;④以点C为圆心,的长为半径作弧,交于点P.下列排序正确的是( )
 A、①②③④ B、②④③① C、③②④① D、④③①②8. 用尺规作图作∠APB的平分线PQ,痕迹如图所示,则此作图的依据是( )
A、①②③④ B、②④③① C、③②④① D、④③①②8. 用尺规作图作∠APB的平分线PQ,痕迹如图所示,则此作图的依据是( ) A、(ASA) B、(SSS) C、(SAS) D、(AAS)
A、(ASA) B、(SSS) C、(SAS) D、(AAS)二、填空题
-
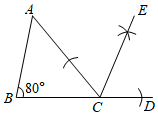
9. 如图,在中, , , 观察图中尺规作图的痕迹,则的度数为 .
 10. 中华人民共和国国旗上的五角星的五个角的和是度.11. 在x轴,y轴上分别截取 ,再分别以点A,B为圆心,以大于 长为半径画弧,两弧交于点P,若点P的坐标为 ,则a的值是.12. 如图,在 中, 以点 为圆心,适当长为半径画弧,分别交 于点 ,再分别以点 为圆心,大于 的长为半径画弧,两弧交于点 ,作射线 射线 与 交于点 ,若 ,则 .
10. 中华人民共和国国旗上的五角星的五个角的和是度.11. 在x轴,y轴上分别截取 ,再分别以点A,B为圆心,以大于 长为半径画弧,两弧交于点P,若点P的坐标为 ,则a的值是.12. 如图,在 中, 以点 为圆心,适当长为半径画弧,分别交 于点 ,再分别以点 为圆心,大于 的长为半径画弧,两弧交于点 ,作射线 射线 与 交于点 ,若 ,则 . 13. 如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画出个.
13. 如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画出个.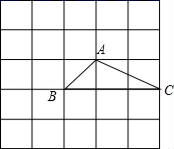
三、解答题
-
14. 如图,在 中, , ,请利用尺规作图法在边BC上找一点D,使得 .(保留作图痕迹,不写作法)
 15. 如图,利用尺规,在的边AC上方作 , 若 , 证明:(尺规作图要求保留作图痕迹,不写作法).
15. 如图,利用尺规,在的边AC上方作 , 若 , 证明:(尺规作图要求保留作图痕迹,不写作法).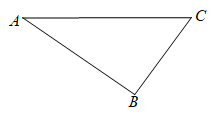
四、作图题
-
16. 作图题(要求:用尺规作图,不写作法,保留作图痕迹).
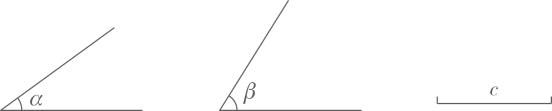
已知: , , 线段 .
求作: , 便 , , .
五、综合题