2023-2024学年初中数学八年级上册 2.4 线段的垂直平分线 同步分层训练培优卷(湘教版)
试卷更新日期:2023-12-11 类型:同步测试
一、选择题
-
1. 如图,在中,是边的垂直平分线,分别交于D、E两点,连接 , , , 则的度数为( )
 A、 B、 C、 D、2. 如图,用直尺和圆规作的角平分线,根据作图痕迹,下列结论不一定正确的是( )
A、 B、 C、 D、2. 如图,用直尺和圆规作的角平分线,根据作图痕迹,下列结论不一定正确的是( )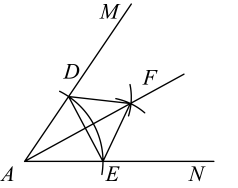 A、 B、 C、 D、3. 如图,三座商场分别坐落在A、B、C所在位置,现要规划一个地铁站,使得该地铁站到三座商场的距离相等,该地铁站应建在( )
A、 B、 C、 D、3. 如图,三座商场分别坐落在A、B、C所在位置,现要规划一个地铁站,使得该地铁站到三座商场的距离相等,该地铁站应建在( ) A、三角形三条中线的交点 B、三角形三条高所在直线的交点 C、三角形三个内角的角平分线的交点 D、三角形三条边的垂直平分线的交点4. 在中, , , 是上的一点,若的周长比的周长大3,根据下列尺规作图痕迹可以得到符合条件的的是( )A、
A、三角形三条中线的交点 B、三角形三条高所在直线的交点 C、三角形三个内角的角平分线的交点 D、三角形三条边的垂直平分线的交点4. 在中, , , 是上的一点,若的周长比的周长大3,根据下列尺规作图痕迹可以得到符合条件的的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,在中,分别以点和点为圆心,大于长为半径画弧,两弧相交于点 , 。作直线 , 交于点 , 交于点 , 连接。若 , , , 则的周长为( )
5. 如图,在中,分别以点和点为圆心,大于长为半径画弧,两弧相交于点 , 。作直线 , 交于点 , 交于点 , 连接。若 , , , 则的周长为( ) A、25 B、22 C、20 D、146. 如图所示的是A、B、C三点,按如下步骤作图:①先分别以A、B两点为圆心,以大于的长为半径作弧,两弧相交于M、N两点,作直线;②再分别以B、C两点为圆心,以大于的长为半径作弧,两弧相交于G、H两点,作直线 , 与交于点P,若 , 则等于( )
A、25 B、22 C、20 D、146. 如图所示的是A、B、C三点,按如下步骤作图:①先分别以A、B两点为圆心,以大于的长为半径作弧,两弧相交于M、N两点,作直线;②再分别以B、C两点为圆心,以大于的长为半径作弧,两弧相交于G、H两点,作直线 , 与交于点P,若 , 则等于( ) A、100° B、120° C、132° D、140°7. 阅读以下尺规作图的步骤:
A、100° B、120° C、132° D、140°7. 阅读以下尺规作图的步骤:
(1)作射线 , 在射线上截取(2)分别以点、为圆心,大于的长为半径作弧,两弧相交于点、(3)作直线交于点(4)在直线上截取(5)连接 ,则可以说明的依据是( )

A、线段垂直平分线上的点到这条线段两个端点的距离相等 B、角平分线上的点到这个角的两边的距离相等 C、等腰三角形的“三线合一” D、平面内,过一点有且只有一条直线与已知直线垂直8. 对于直线L和直线L外的一点O,按下列步骤完成了尺规作图:(1)在直线L的另一侧取点M;(2)以O为圆心,为半径作弧与L交于A,B两点;(3)分别以A,B为圆心,大于为半径作弧,两弧交于点C;(4)过点O和C作直线m.问题:“在直线m上任取一点P(点P不在L上),连接 , , 过点A作直线n与直线垂直,设是 , 直线n与所夹的锐角是 , 求x与y的数量关系.”下面是三个同学的答案,甲: , 乙: , 丙: .对于三人的答案,下列结论正确的是( )
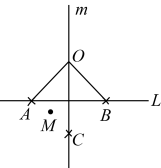 A、只有甲的答案正确 B、甲和乙的答案合在一起才正确 C、甲和丙的答案合在一起才正确 D、甲乙丙的答案合在一起才正确
A、只有甲的答案正确 B、甲和乙的答案合在一起才正确 C、甲和丙的答案合在一起才正确 D、甲乙丙的答案合在一起才正确二、填空题
-
9. 如图,中, , , 的垂直平分线分别交 , 于点 , , 的垂直平分线分别交 , 于点 , , 连接 , , 则 .
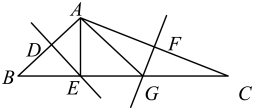 10. 如图,在中,分别以点 , 为圆心,大于的一半为半径作弧,两弧交于点 , , 直线交于点 , 连接 . 若 , , 则的周长等于 .
10. 如图,在中,分别以点 , 为圆心,大于的一半为半径作弧,两弧交于点 , , 直线交于点 , 连接 . 若 , , 则的周长等于 . 11. 如下图,在△ABC中,AB=AC,BC=6,△ABC面积为12,AD⊥BC于点D,直线EF垂直平分AB交AB于点E,交BC于点F,P为直线EF上一动点,则△PBD的周长的最小值为。
11. 如下图,在△ABC中,AB=AC,BC=6,△ABC面积为12,AD⊥BC于点D,直线EF垂直平分AB交AB于点E,交BC于点F,P为直线EF上一动点,则△PBD的周长的最小值为。
 12. 如图,已知三内角的角平分线交于点D,三边的垂直平分线交于点E,若 , 则度.
12. 如图,已知三内角的角平分线交于点D,三边的垂直平分线交于点E,若 , 则度. 13. 如图,在锐角△ABC中,∠ABC=30°,AC=3,△ABC的面积为8,P为△ABC内部一点,分别作点P关于AB,BC,AC的对称点P1 , P2 , P3 , 连接P1P2 , PP3 , 则2P1P2+PP3的最小值为 .
13. 如图,在锐角△ABC中,∠ABC=30°,AC=3,△ABC的面积为8,P为△ABC内部一点,分别作点P关于AB,BC,AC的对称点P1 , P2 , P3 , 连接P1P2 , PP3 , 则2P1P2+PP3的最小值为 .
三、解答题
-
14. 在等腰三角形中, , 垂直平分 , 已知 , 求 .
 15. 根据以下素材,探索完成任务.
15. 根据以下素材,探索完成任务.三角形背景下角的关系探索
素材1
如图,已知等腰△ABC中,BA=BC,在腰BC的延长线上取点E,连结AE,作AE的中垂线交射线BC于点D,连结AD.

素材2
研究一个几何问题时,一般先根据几何语言画出几何图形.可能需要分类讨论.
素材3
当我们要论证一个一般性结论时,常常将问题先分成几种特例,在研究特例的过程中寻求规律,总结方法,猜测结论,再将规律、方法和结论迁移到一般情形中,这种数学推理方法叫做归纳法.
问题解决
任务1
补全图形
请根据素材1,把图形补全.你画的点D在点C的 ▲ 侧.
任务2
特例猜想
有下列条件:①AB=AC;②∠B=40°;③∠CEA=20°;④∠CEA=50°;请从中选择你认为合适的一个或两个条件作为已知条件,求出∠BAD和∠CAE的大小,并猜测∠BAD与∠CAE的数量关系.
任务3
一般结论
请根据你在任务1中所画的一般情况下的图形,写出∠BAD与∠CAE的数量关系,并说明理由.
任务4
拓展延伸
除了你在任务1中所画的情形外,点D相对于点C的位置还有不同的情形吗?若有,请画出图形,并直接写出∠BAD与∠CAE的数量关系.
四、综合题
-
16. 如图,在中,已知 , 是边上的中线,点是边上一动点,点是上的一个动点.
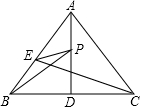 (1)、若 , 求的度数;(2)、若 , , , 且时,求的长;(3)、在(2)的条件下,请直接写出的最小值.17. 综合与实践:
(1)、若 , 求的度数;(2)、若 , , , 且时,求的长;(3)、在(2)的条件下,请直接写出的最小值.17. 综合与实践:已知,等腰三角形纸片ABC中,AB=AC,∠BAC=36°.现要将其剪成三张小纸片,使每张小纸片都是等腰三角形(不能有剩余).下面是小文借助尺规解决这一问题的过程,请阅读后完成相应任务.

作法:如图1所示,
①分别作AB,AC的垂直平分线,交于点P;
②连接PA,PB,PC.
结论:沿线段PA,PB,PC剪开,即可得到三个等腰三角形,
理由:∵点P在线段AB的垂直平分线上,
∴…….. (依据).
同理,PA=PC.
∴PA=PB=PC.
∴△PAB、△PBC、△PAC都是等腰三角形
任务:
(1)、上述过程中,横线上的结论为 , 括号中的依据为 .(2)、受小文的启发,同学们想到另一种思路:如图2,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E.在此基础上构造两条线段(以图中标有字母的点为端点)作为裁剪线,也可解决问题!请在图2中画出一种裁剪方案,直接写出得到的三个等腰三角形及相应顶角的度数.(3)、如图3,等腰三角形纸片ABC中,AB=AC,∠BAC=108°,请从A,B两题中任选一题作答、我选择题.A.请在图3中设计出一种裁剪方案,将该三角形纸片分成三个等腰三角形(要求:尺规作图,保留作图痕迹,不写作法,说明裁剪线).
B.请在图3中设计出一种裁剪方案,将该三角形纸片分成四个等腰三角形,且四个三角形互不全等(要求:尺规作图,保留作图痕迹,不写作法,说明裁剪线).