2023-2024学年初中数学八年级上册 2.3 等腰三角形 同步分层训练培优卷(湘教版)
试卷更新日期:2023-12-11 类型:同步测试
一、选择题
-
1. 等腰三角形两边长分别为5和8,则这个等腰三角形的周长为( )A、18 B、21 C、20 D、18或212. 如图,将等边三角形纸片折叠,使得点A的对应点D落在边上,其中折痕分别交边于点E,F,连接 . 若 , 则的度数是( )
 A、 B、 C、 D、3. 如图,小明荡秋千,位置从A点运动到了点,若 , 则秋千旋转的角度为( )
A、 B、 C、 D、3. 如图,小明荡秋千,位置从A点运动到了点,若 , 则秋千旋转的角度为( ) A、 B、 C、 D、4. 由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小颖同学设计一种衣架,在使用时能轻易收拢,然后秦进衣服后松开即可.如图①,衣架杆(为衣架的固定点);如图②,若衣架收拢时, , 则此时 , 两点之间的距离是( )
A、 B、 C、 D、4. 由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小颖同学设计一种衣架,在使用时能轻易收拢,然后秦进衣服后松开即可.如图①,衣架杆(为衣架的固定点);如图②,若衣架收拢时, , 则此时 , 两点之间的距离是( ) A、 B、 C、 D、5. 如图,直线 , 点 , 分别在 , 上,以点为圆心,长为半径画弧,交于点 , 连接 . 若 , 则的度数为( )
A、 B、 C、 D、5. 如图,直线 , 点 , 分别在 , 上,以点为圆心,长为半径画弧,交于点 , 连接 . 若 , 则的度数为( ) A、10° B、15° C、20° D、25°6. 如图,△ABC中∠A=110°,若图中沿虚线剪去∠A,则∠1+∠2 等于( ).
A、10° B、15° C、20° D、25°6. 如图,△ABC中∠A=110°,若图中沿虚线剪去∠A,则∠1+∠2 等于( ). A、110° B、180° C、290° D、310°7. 如图,已知中, , , 将绕点逆时针旋转得到 , 以下结论:① , ② , ③ , ④ , 正确的有( )
A、110° B、180° C、290° D、310°7. 如图,已知中, , , 将绕点逆时针旋转得到 , 以下结论:① , ② , ③ , ④ , 正确的有( ) A、①②③ B、①②④ C、①③④ D、②③④8. 有一块边长为 的等边三角形纸板,如图1,经过底边的中点剪去第一个正三角形;如图2,过剩余底边的中点再剪去第二个正三角形,然后依次过剩余底边的中点再剪去更小的第三个第四···正三角形,则剪掉的第 个正三角形的面积是( )
A、①②③ B、①②④ C、①③④ D、②③④8. 有一块边长为 的等边三角形纸板,如图1,经过底边的中点剪去第一个正三角形;如图2,过剩余底边的中点再剪去第二个正三角形,然后依次过剩余底边的中点再剪去更小的第三个第四···正三角形,则剪掉的第 个正三角形的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,将等边△ABC折叠,使点B恰好落在AC边上的点D处,折痕为EF,O为折痕EF上的动点,若AD=2,AC=6,则△OCD的周长最小值为 .
 10. 定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做倍长三角形.若等腰是倍长三角形,腰的长为10,则底边的长为 .11. “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒 , 组成,两根棒在点相连并可绕转动,点固定, , 点、可在槽中滑动.若 , 则的度数是 .
10. 定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做倍长三角形.若等腰是倍长三角形,腰的长为10,则底边的长为 .11. “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒 , 组成,两根棒在点相连并可绕转动,点固定, , 点、可在槽中滑动.若 , 则的度数是 . 12. 如图, , 点在射线上,点在射线上,均为等边三角形,从左起第1个等边三角形的边长记为 , 第2个等边三角形的边长记为 , 以此类推,若 , 则 .
12. 如图, , 点在射线上,点在射线上,均为等边三角形,从左起第1个等边三角形的边长记为 , 第2个等边三角形的边长记为 , 以此类推,若 , 则 .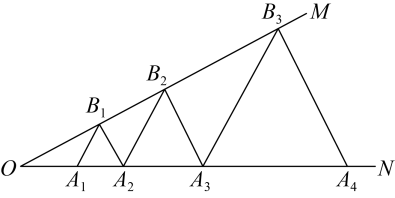 13. 如图,锐角内有一定点A,连接 , 点B、C分别为、边上的动点,连接、、 , 设(),当取得最小值时,则 . (用含的代数式表示)
13. 如图,锐角内有一定点A,连接 , 点B、C分别为、边上的动点,连接、、 , 设(),当取得最小值时,则 . (用含的代数式表示)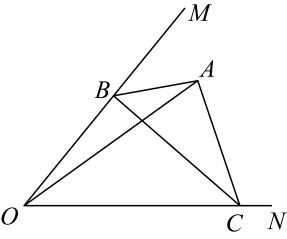
三、解答题
-
14. 如图,在中, , 分别平分和 , 过点作 , 分别交边于点和点 , 如果的周长等于14,的周长等于9,求的长.
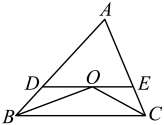 15. 阅读、填空并将说理过程补充完整:如图,已知点D、E分别在△ABC的边AB、AC上,且∠AED=∠B,延长DE与BC的延长线交于点F,∠BAC和∠BFD的角平分线交于点G.那么AG与FG的位置关系如何?为什么?
15. 阅读、填空并将说理过程补充完整:如图,已知点D、E分别在△ABC的边AB、AC上,且∠AED=∠B,延长DE与BC的延长线交于点F,∠BAC和∠BFD的角平分线交于点G.那么AG与FG的位置关系如何?为什么?解:AG⊥FG.将AG、DF的交点记为点P,延长AG交BC于点Q.
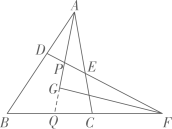
因为AG、FG分别平分∠BAC和∠BFD(已知)
所以∠BAG= ▲ , ▲ (角平分线定义)
又因为∠FPQ= ▲ +∠AED, ▲ = ▲ +∠B
(三角形的一个外角等于与它不相邻的两个内角的和)
∠AED=∠B(已知)
所以∠FPQ= ▲ (等式性质)
(请完成以下说理过程)
四、综合题