2023-2024学年初中数学八年级上册 2.2 命题与证明同步分层训练基础卷(湘教版)

试卷更新日期：2023-12-11 类型：同步测试

进入出卷网下载

一、选择题

1. 下列命题为假命题的是（）

A、垂线段最短 B、同旁内角互补 C、对顶角相等 D、两直线平行，同位角相等

查看试题解析
2. 用反证法证明“若 $a ∥ b ， b ∥ c$ ，则 $a ∥ c$ ”时，应假设（）

A、a与c不平行 B、 $a ∥ c$ C、 $a ⊥ c$ D、a与b不平行，b与c不平行

查看试题解析
3. 下列是真命题的是（）

A、有理数与数轴上的点一一对应 B、内错角相等 C、同一平面内，垂直于同一条直线的两条直线互相平行 D、负数没有立方根

查看试题解析
4. 用反证法证明“在 $△ A B C$ 中，若 $A B = A C$ ，则 $∠ B < 90 °$ ”时，以下三个步骤正确的排列顺序是（）
步骤如下：
①假设在△ABC中，∠B≥90° .
②因此假设不成立，：∴∠B<90°.
③由AB=AC，得∠B=∠C≥90°，即∠B+∠C≥180°，∴∠A+∠B+∠C> 180°，这与“三角形三个内角的和等于180°”产生矛盾.

A、①③② B、①②③ C、③①② D、③②①

查看试题解析
5. 下列说法中①不相交的两条直线叫做平行线；②对顶角的角平分线在同一直线上；③过一点有且只有一条直线与已知直线平行；④几个有理数相乘，积的符号有负因数的个数确定．正确的个数有 ( )

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 可以用来证明命题“任何偶数都是8的倍数”是假命题的反例是：取这个数为（）

A、8 B、4 C、9 D、16

查看试题解析
7. 用反证法证明“在直角三角形中，至少有一个锐角不大于 $45 °$ ”时，应假设直角三角形中（）

A、两个锐角都大于45° B、有一个锐角小于45° C、两个锐角都小于45° D、有一个锐角大于45°

查看试题解析
8. 下列选项中，能说明命题“两个锐角的和是锐角”是一个假命题的反例是（）

A、 $∠ A = 20 ° ， ∠ B = 60 °$ B、 $∠ A = 50 ° ， ∠ B = 90 °$ C、 $∠ A = 40 ° ， ∠ B = 50 °$ D、 $∠ A = 40 ° ， ∠ B = 100 °$

查看试题解析

二、填空题

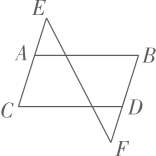
9. 命题“如果x²=9，那么x=3”是命题(填“真”或“假”).

查看试题解析
10. 把命题“对顶角相等”改写成“如果……，那么……”的形式为．

查看试题解析
11. 请写出命题“如果 $a > b$ ，那么 $b - a < 0$ ”的逆命题是．

查看试题解析
12. 举一个反例说明“ $\sqrt{x^{2}} = x$ ”是不成立的，则 $x$ 的值可以是.

查看试题解析
13. 如图，现有以下3个论断：① $A B ∥ C D$ ；② $∠ B = ∠ C$ ；③ $∠ E = ∠ F$ ．如果以其中2个论断为条件，另一个论断为结论构造命题，能够构成个真命题．

查看试题解析

三、解答题

14. 用反证法证明：一个三角形中不能有两个角是直角．
已知： $∠ A$ ， $∠ B$ ， $∠ C$ 是 $△ A B C$ 的三个内角．
求证： $∠ A$ ， $∠ B$ ， $∠ C$ 中不能有两个角是直角．

查看试题解析
15. 阅读材料：怎样证实“两直线平行，同位角相等”
本节中，我们用叠合的方法发现了“两直线平行，同位角相等” .事实上，这个结论可以运用已有的基本事实，通过说理加以证实.
如图，直线AB、CD被直线EF所截，AB//CD，∠1与∠2是同位角.
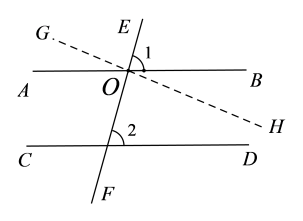
假设∠1 $\neq$ ∠2，那么可以通过直线AB与EF的交点O作直线GH，使∠EOH=∠2，直线GH与直线AB是两条直线.
根据基本事实“同位角相等，两直线平行”，由∠EOH=∠2，可以得到GH//CD.
这样，过点O就有两条直线AB、GH都与CD平行.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”矛盾.
这说明∠1 $\neq$ ∠2的假设不正确，于是∠1=∠2.
解决问题：若 $x \neq 0$ 且 $y \neq 0$ ，请你用以上方法说明： $x^{2} + y^{2} \neq {(x + y)}^{2}$ .

查看试题解析

四、综合题

16. 在数学课上，老师提出了这样一个问题：
如图，点 $E$ 在 $A B$ 的延长线上，请从① $A B ∥ C D$ ；② $A C ∥ B D$ ；③ $∠ D B E + ∠ C = 180 °$ 中，选取两个作为题设，第三个作为结论，组成一个命题，判断其真假，并证明．

小明的做法如下：选取①②作为题设，③作为结论．即“如果 $A B ∥ C D$ ， $A C ∥ B D$ ，那么 $∠ D B E + ∠ C = 180 °$ ”是一个真命题．

证明： $∵ A B ∥ C D$

      $∴ ∠ A + ∠ C = 180 °$ （Ⅰ）

      $∵ A C ∥ B D$

      $∴ ∠ A =$       Ⅱ            （Ⅱ）

      $∴ ∠ D B E + ∠ C = 180 °$ （等量代换）

(1)、请帮助小明补全证明过程及推理依据；

(2)、请作出与小明不同的选择，组成一个新的命题，判断其真假，并证明．

查看试题解析
17. 求证：顶角是锐角的等腰三角形腰上的高与底边夹角等于其顶角的一半．

(1)、根据题意补全下图，并根据题设和结论，结合图形，用符号语言补充写出“已知”和“求证”．
已知：在锐角 $△ A B C$ 中， $A B = A C$ ， ▲ ；
求证： ▲ ．

(2)、证明：

查看试题解析

2023-2024学年初中数学八年级上册 2.2 命题与证明 同步分层训练基础卷(湘教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学八年级上册 2.2 命题与证明同步分层训练基础卷(湘教版)