2023-2024学年初中数学八年级上册 2.1 三角形 同步分层训练培优卷(湘教版)
试卷更新日期:2023-12-11 类型:同步测试
一、选择题
-
1. 三角形的两边分别为3,5,那么它的第三边可以是( )A、1 B、2 C、3 D、82. 若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是( )A、60° B、50° C、40° D、30°3. 如图,在中, , 是的高线,是的角平分线,则的度数是( )
 A、 B、 C、 D、4. 如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1 , 得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2 , 得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3 , 得第3条线段A2A3…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=( )
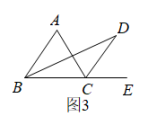
A、 B、 C、 D、4. 如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1 , 得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2 , 得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3 , 得第3条线段A2A3…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=( )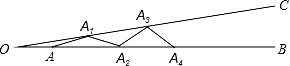 A、10 B、9 C、8 D、75. 长度分别为3cm,5cm,7cm,9cm的四根木棒,能搭成(首尾连接)三角形的个数为( )A、1 B、2 C、3 D、46. 如图,D为边BC延长线上一点,与的平分线交于点 , 与的平分线交于点与的平分线交于点 , 若 , 则的值为( )
A、10 B、9 C、8 D、75. 长度分别为3cm,5cm,7cm,9cm的四根木棒,能搭成(首尾连接)三角形的个数为( )A、1 B、2 C、3 D、46. 如图,D为边BC延长线上一点,与的平分线交于点 , 与的平分线交于点与的平分线交于点 , 若 , 则的值为( ) A、 B、 C、 D、7. 用12根等长的火柴棒拼成一个三角形,火柴棒不允许剩余,重叠和折断,则能摆出不同的三角形的个数是( )A、1个 B、2个 C、3个 D、4个8. 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE中点,且△ABC的面积等于4cm2 , 则阴影部分图形面积等于( ).
A、 B、 C、 D、7. 用12根等长的火柴棒拼成一个三角形,火柴棒不允许剩余,重叠和折断,则能摆出不同的三角形的个数是( )A、1个 B、2个 C、3个 D、4个8. 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE中点,且△ABC的面积等于4cm2 , 则阴影部分图形面积等于( ).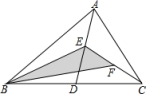 A、1cm2 B、2cm2 C、0.5cm2 D、1.5cm2
A、1cm2 B、2cm2 C、0.5cm2 D、1.5cm2二、填空题
-
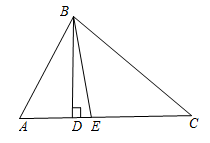
9. 如图,直线 , 且于点C,若 , 则的度数为.
 10. 如图, , , 点B在射线上,若为钝角三角形,则线段长的取值范围是.
10. 如图, , , 点B在射线上,若为钝角三角形,则线段长的取值范围是. 11. 如图,在锐角三角形中, , , 平分 , 若、分别是、上的动点,则的最小值是 .
11. 如图,在锐角三角形中, , , 平分 , 若、分别是、上的动点,则的最小值是 . 12. 已知△ABC中,∠A=∠B=∠C,则△ABC是 三角形.
12. 已知△ABC中,∠A=∠B=∠C,则△ABC是 三角形.三、解答题
-
13. 小明在学习过程中,对教材中的一个有趣问题做如下探究:
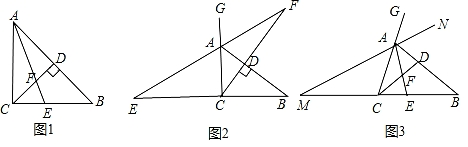
【习题回顾】已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
【变式思考】如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
【探究延伸】如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
14. 学习了平行线的判定与性质后,某兴趣小组提出如下问题: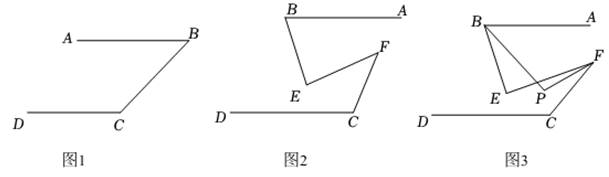
已知:如图, .
【初步感知】如图1,若 , 求的度数;
【拓展延伸】如图2,当点、在两平行线之间,且在位于异侧时,求证:;
【类比探究】如图3,若 , , 若 , , 直接写出的度数.
四、综合题