2023-2024学年广东省(人教版)八年级(上)数学期末模拟卷(二)
试卷更新日期:2023-12-11 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 一个多边形的内角和等于900°,则这个多边形的边数是( )A、5 B、6 C、7 D、无法确定2. 已知P(a , 2)和Q(1,b)关于y轴对称,则(a+b)2021的值为( )A、1 B、-1 C、32021 D、-320213. 已知,中 , , 的对边分别是a , b , c , 下列条件不能判断是直角三角形的是( )A、 B、 C、 , , D、 , ,4. 要使分式有意义,则x应满足的条件是( )A、 B、 C、 D、5. 若 , 则的值为( )A、 B、 C、 D、6. 如图,蝴蝶剪纸是一副轴对称图形,将其放在平面直角坐标系中,如果图中点E的坐标为 , 其关于y轴对称的点F的坐标为 , 则的值为( )
 A、 B、1 C、 D、57. 如图,在的正方形方格中,每个小正方形方格的边长都为1,则和的关系是( )
A、 B、1 C、 D、57. 如图,在的正方形方格中,每个小正方形方格的边长都为1,则和的关系是( ) A、 B、 C、 D、8. 下列说法正确的是( )A、如果两个三角形的周长相等,那么这两个三角形一定全等 B、同位角相等 C、在同一平面内经过直线外一点有且只有一条直线与已知直线平行 D、一个角的补角一定是钝角9. 下列事件是必然事件的是( )A、购买一张体育彩票,中奖 B、任意掷一枚色子,其点数为奇数 C、打开电视机,任选一个频道,屏幕上正在播放新闻联播 D、任意画一个三角形,其内角和是180°10. 如图,OP平分∠MON , PA⊥ON于点A , 若PA=2,则PQ最小值为( )
A、 B、 C、 D、8. 下列说法正确的是( )A、如果两个三角形的周长相等,那么这两个三角形一定全等 B、同位角相等 C、在同一平面内经过直线外一点有且只有一条直线与已知直线平行 D、一个角的补角一定是钝角9. 下列事件是必然事件的是( )A、购买一张体育彩票,中奖 B、任意掷一枚色子,其点数为奇数 C、打开电视机,任选一个频道,屏幕上正在播放新闻联播 D、任意画一个三角形,其内角和是180°10. 如图,OP平分∠MON , PA⊥ON于点A , 若PA=2,则PQ最小值为( )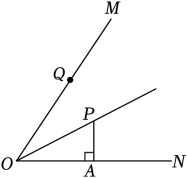 A、3 B、2 C、1 D、1.5
A、3 B、2 C、1 D、1.5二、填空题(每题3分,共15分)
-
11. 已知一个三角形的三边长为3,8,a,则a的取值范围是 .12. 若 , , 则xy= .13. 如图,直线AB的解析式为y=-x+b , 分别与x轴,y轴交于A , B两点,点A的坐标为(4,0),过点B的直线交x轴负半轴于点C , 且OB:OC=4:1.若在x轴上方存在点D , 使以A , B , D为顶点的三角形与△ABC全等,则点D的坐标为 .
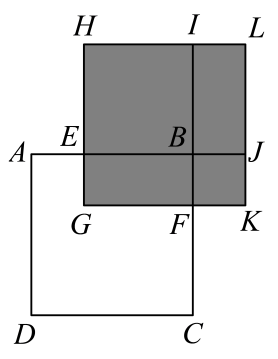
 14. 如图,在中, , 分别以为边向上作正方形、正方形、正方形 , 点在上,若 , 则图中阴影的面积为 .
14. 如图,在中, , 分别以为边向上作正方形、正方形、正方形 , 点在上,若 , 则图中阴影的面积为 . 15. 如图,在锐角△ABC中,BC=4,∠ABC=30°,∠ABD=15°,直线BD交边AC于点D,点P、Q分别在线段BD、BC上运动,则PQ+PC的最小值是 .
15. 如图,在锐角△ABC中,BC=4,∠ABC=30°,∠ABD=15°,直线BD交边AC于点D,点P、Q分别在线段BD、BC上运动,则PQ+PC的最小值是 .
三、解答题(共8题,共75分)
-
16. 计算: .17.(1)、解分式方程:;(2)、分解因式: .18. 先化简,再求值: , 其中 .19. 如图,在边长为1的小正方形所组成的网格上,每个小正方形的顶点都称为“格点”,的顶点都在格点上,用直尺完成下列作图.
 (1)、作出关于直线的对称图形;(2)、在网格中建立直角坐标系,使点A坐标为;(3)、在直线上取一点P,使得最小.20. 如图,点B,F,C,E在一直线上, . 求证: .
(1)、作出关于直线的对称图形;(2)、在网格中建立直角坐标系,使点A坐标为;(3)、在直线上取一点P,使得最小.20. 如图,点B,F,C,E在一直线上, . 求证: . 21. 某中学开学初在商场购进A、B两种品牌的足球,购买A品牌足球花费了2500元,购买B品牌足球花费了2000元,且购买A品牌足球数量是购买B品牌足球数量的2倍,已知购买一个B品牌足球比购买一个A品牌足球多花30元.(1)、求购买一个A品牌、一个B品牌的足球各需多少元;(2)、该中学决定再次购进A、B两种品牌足球共50个,恰逢商场对两种品牌足球的售价进行调整,A品牌足球售价比第一次购买时提高了8%,B品牌足球按第一次购买时售价的9折出售,如果这所中学此次购买A、B两种品牌足球的总费用不超过3060元,那么该中学此次最多可购买多少个B品牌足球?22. 如图
21. 某中学开学初在商场购进A、B两种品牌的足球,购买A品牌足球花费了2500元,购买B品牌足球花费了2000元,且购买A品牌足球数量是购买B品牌足球数量的2倍,已知购买一个B品牌足球比购买一个A品牌足球多花30元.(1)、求购买一个A品牌、一个B品牌的足球各需多少元;(2)、该中学决定再次购进A、B两种品牌足球共50个,恰逢商场对两种品牌足球的售价进行调整,A品牌足球售价比第一次购买时提高了8%,B品牌足球按第一次购买时售价的9折出售,如果这所中学此次购买A、B两种品牌足球的总费用不超过3060元,那么该中学此次最多可购买多少个B品牌足球?22. 如图
 (1)、在图1中,请直接写出、、、之间的数量关系:;(2)、仔细观察,在图2中“8字形”的个数 个;(3)、如果图2中, , , 与分别是和的角平分线,试求的度数;(4)、如果图2中和为任意角,其他条件不变,试问与 , 之间存在着怎样的数量关系(直接写出结论即可).23. 阅读材料:若满足 , 求的值.
(1)、在图1中,请直接写出、、、之间的数量关系:;(2)、仔细观察,在图2中“8字形”的个数 个;(3)、如果图2中, , , 与分别是和的角平分线,试求的度数;(4)、如果图2中和为任意角,其他条件不变,试问与 , 之间存在着怎样的数量关系(直接写出结论即可).23. 阅读材料:若满足 , 求的值.解:设 , , 则 ,
所以
请仿照上例解决下列问题:
(1)、若x满足 , 求的值;(2)、若x满足 , 求的值;(3)、如图,正方形的边长为 , , , 长方形的面积是10,四边形和都是正方形,是长方形,求图中阴影部分的面积(结果必须是一个具体的数值).