2023-2024学年广东省（人教版）八年级（上）数学期末模拟卷（一）

试卷更新日期：2023-12-11 类型：期末考试

进入出卷网下载

一、选择题

1. 下面四幅图是我国一些博物馆的标志，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，一束平行太阳光照射到正六边形上，若 $∠ 1 = 2 8^{∘}$ ，则 $∠ 2$ 的大小为（）

A、150° B、148° C、140° D、138°

查看试题解析
3. 如果一个分式的分子或分母可以因式分解，且这个分式不可约分，那么我们称这个分式为“和谐分式”，下列分式中是和谐分式的是（）

A、 $\frac{x^{2} - y^{2}}{{(x + y)}^{2}}$ B、 $\frac{x + y}{x^{2} - y^{2}}$ C、 $\frac{x - 2 y}{x^{2} - y^{2}}$ D、 $\frac{x - 2}{x^{2} + 2}$

查看试题解析
4. 已知一个多边形的内角和为 $720 °$ ，则这个多边形是（）

A、八边形 B、七边形 C、六边形 D、五边形

查看试题解析
5. 点 $A (2 ， 0)$ 关于 $y$ 轴对称的点的坐标是（）

A、 $(0 ， 2)$ B、 $(0 ， - 2)$ C、 $(2 ， 0)$ D、 $(- 2 ， 0)$

查看试题解析
6. 下列由左到右的变形，属于因式分解的是（）

A、 $x^{2} - 4 = (x + 2) (x - 2)$ B、 $(x + 2) (x - 2) = x^{2} - 4$ C、 $x^{2} - 4 + 3 x = (x + 2) (x - 2) + 3 x$ D、 $x^{2} + 4 x - 2 = x (x + 4) - 2$

查看试题解析
7. 如图， $A D$ 是 $△ A B C$ 的中线，E，F分别是 $A D$ 和 $A D$ 延长线上的点，且 $D E = D F$ ，连接 $B F$ ， $C E$ ，下列说法：① $△ A B D$ 和 $△ A C D$ 面积相等；② $∠ B A D = ∠ C A D$ ；③ $△ B D F ≅ △ C D E$ ；④ $B F ∥ C E$ ；⑤ $C E = A E$ ．其中正确的是（　　）

A、①② B、③⑤ C、①③④ D、①④⑤

查看试题解析
8. 小颖的爸爸要在某条街道l上修建一个奶站P，向居民区A，B提供牛奶，要使点P到A，B的距离之和最短，则下列作法正确的是（）

A、 B、 C、 D、

查看试题解析
9. 若整数a使关于y的不等式组 ${\begin{array}{l} \frac{2 y - 5}{3} \leq y - \frac{1}{3} \\ a - y + 3 \geq 0 \end{array}$ 至少有3个整数解，且使得关于x的分式方程 $\frac{3}{x (x - 1)} - \frac{a}{1 - x} = \frac{2}{x}$ 的解为正数，则所有符合条件的整数a的和为（）

A、-6 B、-9 C、-11 D、-14

查看试题解析
10. 随着生活水平的提高，小林家购置了私家车，这样他乘坐私家车上学比乘坐公交车上学所需的时间少用了20分钟，现已知小林家距学校8千米，乘私家车平均速度是乘公交车平均速度的3倍，若设乘公交车平均每小时走 $x$ 千米，根据题意可列方程为（）

A、 $\frac{8}{x} + 20 = \frac{8}{3 x}$ B、 $\frac{8}{x} = \frac{8}{3 x} + \frac{1}{3}$ C、 $\frac{8}{x} = \frac{8}{3 x} + 20$ D、 $\frac{8}{x} + \frac{1}{3} = \frac{8}{3 x}$

查看试题解析

二、填空题

11. 若 $1 0^{m} = 5$ ， $1 0^{n} = 2$ ，则 $1 0^{2 m + 3 n} =$ ．

查看试题解析
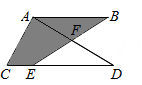
12. 某药品原来每盒p元，现在每盒提高3元，用200元买这种药品现在比原来少买盒．

查看试题解析
13. 如图，在△ACD中， $∠ C A D = 90 °$ ， AC=6，AD=8， $A B ∥ C D$ ， E是CD上一点，BE交AD于点F，若EF=BF，则图中阴影部分的面积为．

查看试题解析
14. 若数 $a$ 使关于 $x$ 的分式方程 $\frac{x + 1}{x - 2} + \frac{a}{2 - x} = 3$ 的解为正数，且使关于 $y$ 的不等式组 ${\begin{array}{l} - 3 (y - 2) \geq 4 - y \\ 3 (y - a) < 0 \end{array}$ 的解集为 $y \leq 1$ ，则符合条件所有整数 $a$ 的积为．

查看试题解析
15. 下列命题：①若|a|=-a，则a<0；②内错角相等；③平行于同一条直线的两条直线平行；④直线a、b、c在同一平面内，若a⊥b，a⊥c，则b $∥$ c；⑤实数包括有理数和无理数．其中正确的命题序号有．

查看试题解析

三、解答题

16. 计算：

(1)、（﹣5y²）³；

(2)、 $\frac{4 x}{3 y}$ • $\frac{y}{2 x^{3}}$ ；

(3)、4（x+1）²﹣（2x+3）（2x﹣3）．

查看试题解析
17. 因式分解：

(1)、 $x^{2} (a - b) + 9 (b - a)$

(2)、 ${(a^{2} + 4)}^{2} - 16 a^{2}$

查看试题解析
18. 如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．

(1)、若△A₁B₁C₁与△ABC关于y轴成轴对称，则△A₁B₁C₁三个顶点坐标分别为A₁ ， B₁ ， C₁；

(2)、在x轴上找一点P，使PA+PB的值最小，请直接写出点P的坐标是．

(3)、在y轴上是否存在点Q．使得S_△_ACQ＝ $\frac{1}{2}$ S_△_ABC ，如果存在，求出点Q的坐标，如果不存在，说明理由．

查看试题解析
19. 如图，在△ABC中，AD⊥BC，垂直为D，∠1=∠B，∠C=67°，求∠BAC的度数

查看试题解析
20. 如图，已知 $A (3 ， 0)$ ， $B (0 ， - 1)$ ，连接 $A B$ ，过B点作 $A B$ 的垂线段 $B C$ ，使 $B A = B C$ ，连接 $A C$ ．

(1)、如图1，求C点坐标；

(2)、如图2，若P点从A点出发沿x轴向左平移，连接 $B P$ ，作等腰直角 $△ B P Q$ ，连接 $C Q$ ，当点P在线段 $O A$ 上，求证： $P A = C Q$ ．

查看试题解析
21. 某校为积极响应垃圾分类的号召，从商场购进了 $A$ 、 $B$ 两种品牌的垃圾桶用于回收不同种类垃圾．已知 $B$ 品牌垃圾桶比 $A$ 品牌垃圾桶每个贵40元，用4800元购买 $A$ 品牌垃圾桶的数量是用3600元购买 $B$ 品牌垃圾桶数量的2倍．

(1)、求购买一个 $A$ 品牌、一个 $B$ 品牌的垃圾桶各需多少元?

(2)、该学校准备再次用不超过5600元购进 $A$ 、 $B$ 两种品牌垃圾桶共50个，恰逢商场对两种品牌垃圾桶的售价进行了调整： $A$ 品牌按第一次购买时售价的八折出售， $B$ 品牌比第一次购买时售价提高了20%，那么该学校此次最多可购买多少个 $B$ 品牌垃圾桶？

查看试题解析

22. 阅读下面材料，在代数式中，我们把一个二次多项式化为一个完全平方式与一个常数的和的方法叫做配方法。配方法是一种重要的解决问题的数学方法，它不仅可以将一个看似不能分解的多项式因式分解，还能求代数式最大值，最小值等问题．

例如：求代数式： $x^{2} - 12 x + 2020$ 的最小值

解：原式 $= x^{2} - 12 x + 6^{2} - 6^{2} + 2020$

$= {(x - 6)}^{2} + 1984$

∵ ${(x - 6)}^{2} \geq 0$

∴当x=6时， ${(x - 6)}^{2}$ 的值最小，最小值为0

∴ ${(x - 6)}^{2} + 1984 \geq 1984$

∴当 ${(x - 6)}^{2} = 0$ 时， ${(x - 6)}^{2} + 1984$ 的值最小，最小值为1984

∴代数式： $x^{2} - 12 x + 2020$ 的最小值是1984

例如：分解因式： $x^{2} - 120 x + 3456$

解：原式 $= x^{2} - 2 \times 60 x + 6 0^{2} - 6 0^{2} + 3456$

$= {(x - 60)}^{2} - 144$

$= {(x - 60)}^{2} - 1 2^{2}$

$= (x - 60 + 12) (x - 60 - 12)$

$= (x - 48) (x - 72)$

(1)、分解因式

x^{2} - 46 x + 520

；

(2)、若

y = - x^{2} + 2 x + 1313

，求y的最大值；

(3)、当m，n为何值时，代数式

m^{2} - 2 m n - 2 m + 2 n^{2} - 4 n + 2030

有最小值，并求出这个最小值．

查看试题解析

23.

(1)、【问题背景】学校数学兴趣小组在专题学习中遇到一个几何问题：如图1，已知等边△ABC，D是△ABC外一点，连接AD、CD、BD，若∠ADC＝30°，AD＝3，BD＝5，求CD的长．该小组在研究如图2中△OMN≌△OPQ中得到启示，于是作出图3，从而获得了以下的解题思路，请你帮忙完善解题过程．
解：如图3所示，以DC为边作等边△CDE，连接AE．
∵△ABC、△DCE是等边三角形，
∴BC＝AC，DC＝EC，∠BCA＝∠DCE＝60°．
∴∠BCA+∠ACD＝                  ▲                   +∠ACD，
∴∠BCD＝∠ACE，
∴                  ▲                   ，
∴AE＝BD＝5．
∵∠ADC＝30°，∠CDE＝60°，
∴∠ADE＝∠ADC+∠CDE＝90°．
∵AD＝3，
∴CD＝DE＝                  ▲                   ．

(2)、【尝试应用】如图4，在△ABC中，∠ABC＝45°，AB＝ $\sqrt{2}$ ， BC＝4，以AC为直角边，A为直角顶点作等腰直角△ACD，求BD的长．

(3)、【拓展创新】如图5，在△ABC中，AB＝4，AC＝8，以BC为边向外作等腰△BCD，BD＝CD，∠BDC＝120°，连接AD，求AD的最大值．

查看试题解析