2023-2024学年广东省(人教版)七年级(上)数学期末模拟卷(三)
试卷更新日期:2023-12-11 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 把数字770506,用科学记数法(保留三个有效数字)表示为( )A、 B、 C、 D、2. 下列运用等式性质进行的变形,正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则3. 如图,从甲地到乙地有四条道路,其中最近的路线是( )
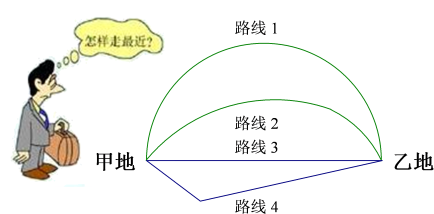 A、路线 B、路线 C、路线 D、路线4. 下列计算正确的是( )A、 B、 C、 D、5. 已知关于x的方程2x+a=1-x与方程2x-3=1的解相同,则a的值为( )A、2 B、-2 C、5 D、-56. 如图,点C、D分别是线段AB上两点(CD>AC,CD>BD),用圆规在线段CD上截取CE=AC,DF=BD, 若点E与点F恰好重合,AB=8,则CD=( )
A、路线 B、路线 C、路线 D、路线4. 下列计算正确的是( )A、 B、 C、 D、5. 已知关于x的方程2x+a=1-x与方程2x-3=1的解相同,则a的值为( )A、2 B、-2 C、5 D、-56. 如图,点C、D分别是线段AB上两点(CD>AC,CD>BD),用圆规在线段CD上截取CE=AC,DF=BD, 若点E与点F恰好重合,AB=8,则CD=( )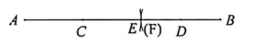 A、4 B、4.5 C、5 D、5.57. 下列说法正确的是( )A、|-2|的相反数是2 B、各边都相等的多边形叫正多边形 C、了解一沓钞票中有没有假钞,应采用普查的形式 D、若线段AB=BC,则点B是线段AC的中点8. 下列角中,能用 , , 三种方法表示同一个角的是( )A、
A、4 B、4.5 C、5 D、5.57. 下列说法正确的是( )A、|-2|的相反数是2 B、各边都相等的多边形叫正多边形 C、了解一沓钞票中有没有假钞,应采用普查的形式 D、若线段AB=BC,则点B是线段AC的中点8. 下列角中,能用 , , 三种方法表示同一个角的是( )A、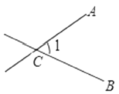 B、
B、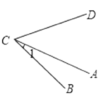 C、
C、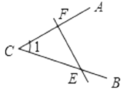 D、
D、 9. 某一品牌的牛奶包装盒,该包装盒可以近似的看成是长方体,则它的展开图不可能是( )A、
9. 某一品牌的牛奶包装盒,该包装盒可以近似的看成是长方体,则它的展开图不可能是( )A、 B、
B、 C、
C、 D、
D、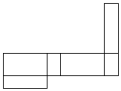 10. 某商店以每个120元的价格卖出两个智能手表,其中一个盈利20%,另一个亏损20%.在这次买卖中,这家商店( )A、不盈不亏 B、亏损10元 C、盈利9.6元 D、亏损9.6元
10. 某商店以每个120元的价格卖出两个智能手表,其中一个盈利20%,另一个亏损20%.在这次买卖中,这家商店( )A、不盈不亏 B、亏损10元 C、盈利9.6元 D、亏损9.6元二、填空题(每题3分,共15分)
-
11. 钟表上显示8:30,时针与分针的夹角为 。12. 用一个平面去截一个正方体,得到的截面的形状可能是:①圆,②三角形,③长方形,④五边形,⑤六边形,⑥七边形其中的 .13. 某商品的进价是2000元,标价为2800元,该商品打多少折才能获得12%的利润率?设该商品需打x折才能使利润率为12%,根据题意列出方程: .14. 王小毛同学做教室卫生时,发现座位很不整齐,他思考了一下,将第一座和最后一座固定之后,沿着第一座最后一座这条线就把座位摆整齐了!他利用了数学原理: .
 15. 如图,已知轮船A在灯塔P的北偏东方向,轮船B在灯塔P的南偏东方向,则的度数是 .
15. 如图,已知轮船A在灯塔P的北偏东方向,轮船B在灯塔P的南偏东方向,则的度数是 .
三、解答题(共8题,共75分)
-
16. 计算下列各式(1)、(2)、117. 解方程:(1)、(2)、18. 如图,△ABC中,∠BAC=90°,点D是BC上的一点,将△ABC沿AD翻折后,点B恰好落在线段CD上的B'处,且AB'平分∠CAD.求∠BAB'的度数.
 19. 随着手机的普及,微信的兴起,许多人做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售.刚大学毕业的小明把自家的冬枣产品也放到了网上实行包邮销售,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况(超额记为正,不足记为负.单位:斤);
19. 随着手机的普及,微信的兴起,许多人做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售.刚大学毕业的小明把自家的冬枣产品也放到了网上实行包邮销售,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况(超额记为正,不足记为负.单位:斤);星期
一
二
三
四
五
六
日
与计划量的差值
(1)、根据记录的数据可知销售量最多的一天比销售量最少的一天多销售斤;(2)、本周实际销售总量是否达到了计划数量?试说明理由;(3)、若冬枣每斤按8元出售,每斤冬枣需要小明支付的平均运费是3元,那么小明本周销售冬枣实际共得多少元?20. 出租车司机李师傅某天下午从停车场出发一直沿东西方向的大街进行营运,规定向东为正,向西为负,他的行驶里程(单位:)记录如下:+10,-6,+3,+12,-12,+5,-13,5.
(1)、当把最后一名乘客送达目的地时,李师傅在停车场的什么位置?(2)、若每千米的营运额为3元,成本为1.5元 , 则这天下午他盈利多少元?21. 一套仪器由一个A部件和三个B部件构成,用1立方米钢材可做40个A部件或240个B部件.现要用6立方米钢材制作这种仪器,应用多少钢材制作A部件,才能使生产的A、B刚好配套?恰好配成这种仪器多少套?22. 七年级学习代数式求值时,遇到这样一类题“代数式的值与的取值无关,求的值”,通常的解题方法是:把x、y看作字母,a看作系数合并同类项,因为代数式的值与x的取值无关,所以含项的系数为0,即原式= , 所以 , 则 .
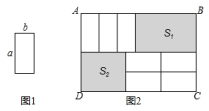 (1)、若关于的多项式的值与的取值无关,求值;(2)、已知A , B;且3A+6B的值与无关,求的值;(3)、7张如图1的小长方形,长为a,宽为b,按照图2方式不重叠地放在大长方形ABCD内,大长方形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为 , 左下角的面积为 , 当AB的长变化时,的值始终保持不变,求与的等量关系.23. 我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离,即|x|=|x﹣0|,也就是说|x|表示在数轴上数x与数0对应点之间的距离;这个结论可以推广为:|x﹣y|表示在数轴上数x、y对应点之间的距离;在解题中,我们常常运用绝对值的几何意义.
(1)、若关于的多项式的值与的取值无关,求值;(2)、已知A , B;且3A+6B的值与无关,求的值;(3)、7张如图1的小长方形,长为a,宽为b,按照图2方式不重叠地放在大长方形ABCD内,大长方形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为 , 左下角的面积为 , 当AB的长变化时,的值始终保持不变,求与的等量关系.23. 我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离,即|x|=|x﹣0|,也就是说|x|表示在数轴上数x与数0对应点之间的距离;这个结论可以推广为:|x﹣y|表示在数轴上数x、y对应点之间的距离;在解题中,我们常常运用绝对值的几何意义.①解方程|x|=2,容易看出,在数轴上与原点距离为2的点对应的数为±2,即该方程的解为x=±2.
②在方程|x﹣1|=2中,x的值就是数轴上到1的距离为2的点对应的数,显然x=3或x=﹣1.
③在方程|x﹣1|+|x+2|=5中,显然该方程表示数轴上与1和﹣2的距离之和为5 的点对应的x值,在数轴上1和﹣2的距离为3,满足方程的x的对应点在1的右边或﹣2的左边.若x的对应点在1的右边,由图示可知,x=2;同理,若x的对应点在﹣2的左边,可得x=﹣3,所以原方程的解是x=2或x=﹣3.根据上面的阅读材料,解答下列问题:
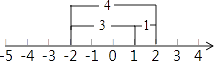 (1)、方程|x|=5的解是 .(2)、方程|x﹣2|=3的解是 .(3)、画出图示,解方程|x﹣3|+|x+2|=9.
(1)、方程|x|=5的解是 .(2)、方程|x﹣2|=3的解是 .(3)、画出图示,解方程|x﹣3|+|x+2|=9.