安徽省安庆市潜山市2023-2024学年九年级上学期期中数学试题
试卷更新日期:2023-12-11 类型:期中考试
一、选择题(本大题共10小题,每小题4分,满分40分,每小题都给出A,B,C,D四个选项,其中只有一个选项是正确的)
-
1. 抛物线的顶点坐标是( )A、 B、 C、 D、2. 下列各组中的四条线段成比例的是( )A、1,2,3,4 B、2,4,3,5 C、4,8,5,10 D、3,9,4,73. 下列各点中,在双曲线的图象上的是( )A、 B、 C、 D、4. 当时,下列函数值y随x增大而增大的是( )A、 B、 C、 D、5. 如图,和是位似图形,点O是位似中心, .若点A的坐标为 , 则点C的坐标为( )
 A、 B、 C、 D、6. 如图,在和中,已知 , 则添加下列条件能判定和相似的是( )
A、 B、 C、 D、6. 如图,在和中,已知 , 则添加下列条件能判定和相似的是( ) A、 B、 C、 D、7. 已知抛物线(a,b,c是常数)的图象如图所示,则下列判断正确的是( )
A、 B、 C、 D、7. 已知抛物线(a,b,c是常数)的图象如图所示,则下列判断正确的是( ) A、 B、 C、 D、8. 平移抛物线使其经过原点,则下列操作不正确的是( )A、向右平移1个单位长度 B、向右平移5个单位长度 C、向下平移5个单位长度 D、向上平移4个单位长度9. 将一张三角形彩纸按如图所示的方式折叠,使点B落在边上,记为点F,折痕为 . 已知 , , 若以点C,D,F为顶点的三角形与相似,则的长是( )
A、 B、 C、 D、8. 平移抛物线使其经过原点,则下列操作不正确的是( )A、向右平移1个单位长度 B、向右平移5个单位长度 C、向下平移5个单位长度 D、向上平移4个单位长度9. 将一张三角形彩纸按如图所示的方式折叠,使点B落在边上,记为点F,折痕为 . 已知 , , 若以点C,D,F为顶点的三角形与相似,则的长是( )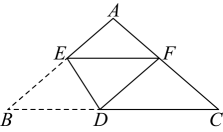 A、 B、 C、 或4 D、 或410. 如图,直线分别交x轴、y轴于点C,D,点P为反比例函数在第一象限内图像上的一点,过点P分别作x轴、y轴的垂线交直线于点A,B,且 , 则下列结论错误的是( )
A、 B、 C、 或4 D、 或410. 如图,直线分别交x轴、y轴于点C,D,点P为反比例函数在第一象限内图像上的一点,过点P分别作x轴、y轴的垂线交直线于点A,B,且 , 则下列结论错误的是( ) A、与相似 B、 C、 D、
A、与相似 B、 C、 D、二、填空题(本大题共4小题,每小题5分,满分20分)
-
11. 若 , 则的值为 .12. 将抛物线关于y轴对称,所得到的抛物线解析式为 .13. 如图,点P是双曲线上的一点,点A,B是x轴正半轴上的不同点,连接AP,BP,已知 , , 的面积为3,则 .
 14. 如图,在正方形中,是边上的一点,连接交于点 , 连接并延长交于点 .
14. 如图,在正方形中,是边上的一点,连接交于点 , 连接并延长交于点 .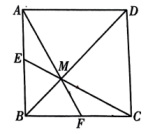 (1)、若是的中点,则;(2)、若 , 则 .
(1)、若是的中点,则;(2)、若 , 则 .三、(本大题共2小题,每小题8分,满分16分)
-
15. 已知抛物线 , 判断该抛物线与x轴的交点情况,并说明理由.16. 如图,在边长为1个单位长度的小正方形组成的的网格中,和的顶点都在网格的格点上.求证: .

四、(本大题共2小题,每小题8分,满分16分)
-
17. 国庆期间,小李自驾小汽车从家到银屏山旅游.查询导航得知,当他的小汽车保持80km/h的速度行驶3h可以到达银屏山.若该小汽车匀速行驶的速度为vkm/h,行驶的时间为th.(1)、求v关于t的函数表达式;(2)、若返回时,该小汽车匀速行驶的速度为60km/h,假设他返回与去时的路况和其他因素一致,求他从银屏山回到家需要几小时.18. 如图,在平面直角坐标系中,的顶点都在网格的格点上,按要求解决下列问题.

⑴画出关于y轴的轴对称图形;
⑵以点O为位似中心,在第一象限中出画出 , 使得与位似,且相似比为 .
五、(本大题共2小题,每小题10分,满分20分)
-
19. 如图,直线与双曲线交于点与点 .
 (1)、直接写出不等式的解集:;(2)、求的面积.20. 如图,四边形是平行四边形,点E是延长线上一点,连接分别与交于点F,G.
(1)、直接写出不等式的解集:;(2)、求的面积.20. 如图,四边形是平行四边形,点E是延长线上一点,连接分别与交于点F,G. (1)、若 , , 求的长;(2)、求证: .
(1)、若 , , 求的长;(2)、求证: .六、(本题满分12分)
-
21. 某工厂生产地方特色手工老棉鞋,它的成本价为20元/双.该工厂利用网络平台销售某一批老棉鞋,每天销售量y(双)与销售单价x(元)之间的函数图象如图,已知图象是直线的一部分.
 (1)、求y与x之间的函数表达式;(2)、若该工厂要求每天销售量不低于320双,当销售单价为多少元时,每天获得的利润最大,最大利润是多少元?
(1)、求y与x之间的函数表达式;(2)、若该工厂要求每天销售量不低于320双,当销售单价为多少元时,每天获得的利润最大,最大利润是多少元?七、(本题满分12分)



