安徽省合肥市包河区2023-2024学年七年级上学期期中数学试题

试卷更新日期：2023-12-11 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分）

1. -5的倒数是（）.

A、 $- \frac{1}{5}$ B、5 C、 $\frac{1}{5}$ D、-5

查看试题解析
2. 下列各式中不成立的是（）.

A、 $| - 5 | = 5$ B、 $- | 5 | = - | - 5 |$ C、 $- | - 5 | = 5$ D、 $- (- 5) = 5$

查看试题解析
3. 据媒体报道，我国因环境污染造成的巨大经济损失，每年高达680000000元，这个数用科学记数法表示正确的是（）

A、6.8×10⁹元 B、6.8×10⁸元 C、6.8×10⁷元 D、6.8×10⁶元

查看试题解析
4. 下列说法正确的是（）.

A、所有的整数都是正数 B、整数、0和分数统称为有理数 C、0是最小的有理数 D、-1是最大的负整数

查看试题解析
5. 一批螺帽产品的内径要求可以有 $\pm 0.03 m m$ 的误差，现抽查5个样品，超过规定的毫米值记为正数，不足值记为负数，检查结果如表.则合乎要求的产品数量为（）.
1
2
3
4
5
+0.031
+0.017
+0.023
-0.021
-0.015

A、2个 B、3个 C、4个 D、5个

查看试题解析
6. 如果方程 $2 x = 4$ 与方程 $3 x + k = - 2$ 的解相同，则k的值为（）.

A、-8 B、-4 C、4 D、8

查看试题解析
7. 点A在数轴上，点A所对应的数用 $2 a + 1$ 表示，且点A到原点的距离等于3，则a的值为（）

A、-2或1 B、-2或2 C、-2 D、1

查看试题解析
8. 若 $| x - 3 | + {(y + 4)}^{2} = 0$ ，则 ${(x + y)}^{2023}$ 的值为（）.

A、1 B、-1 C、2023 D、-2023

查看试题解析
9. 按照如图所示的操作步骤，若输入值为-5，则输出的值为（）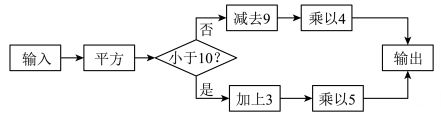

A、140 B、64 C、-64 D、-140

查看试题解析
10. 幻方是古老的数学问题，我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中，要求每一横行、每一竖列以及两条对角线上的3个数之和相等，例如图（1）就是一个幻方.图（2）是一个未完成的幻方，则 $x$ 与 $y$ 的和是（）

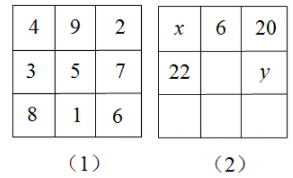A、9 B、10 C、11 D、12

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

11. 比较大小：-3.3-3.14.

查看试题解析
12. 已知 $- 25 a^{2 m} b$ 和 $7 a^{4} b^{n}$ 是同类项，则 $m + n$ 的值是.

查看试题解析
13. 按括号内的要求，用四舍五入法取308.607的近似数（精确到个位）是.

查看试题解析
14. 已知a，b互为相反数，c，d互为倒数， $| m | = 2$ ，则 $\frac{a + b}{m} - m^{2} + 2 c d$ 的值是.

查看试题解析
15. 观察下列各数：1， $- \frac{1}{3}$ ， $\frac{2}{5}$ ， $- \frac{2}{7}$ ， $\frac{1}{3}$ ， $- \frac{3}{11}$ ， …，依照这样的规律第2023个数是.

查看试题解析
16. 已知 $a^{2} + 2 a b = - 2$ ， $a b - b^{2} = - 4$ ，则 $2 a^{2} + \frac{7}{2} a b + \frac{1}{2} b^{2}$ 的值为.

查看试题解析

三、（本大题共3小题，满分25分）

17. 计算：

(1)、 $- 16 - (- 12) - 24 + 18$

(2)、 $- 6^{2} \times (- \frac{7}{12} - \frac{13}{36} + \frac{5}{6})$

查看试题解析
18. 解方程：

(1)、 $2 x + 1 = - 2 - 3 x$

(2)、 $x + \frac{1 - 2 x}{3} = 2 - \frac{x + 2}{2}$

查看试题解析
19. 足球比赛中，根据场上攻守形势，守门员会在门前来回跑动，如果以球门线为基准，向前记作正数，返回则记作负数，一段时间内，某守门员的跑动情况记录如下（单位：m）：+7，-3，+8，+4，-6，-8，+14，-15.（假定开始时，守门员正好在球门线上）

(1)、守门员最后是否回到球门线上？

(2)、假设守门员每跑1米消耗0.1卡路里的能量，守门员在这段时间内共消耗了多少卡路里的能量？

(3)、如果守门员离开球门线的距离超过10m（不包括10m），则对方球员挑射极可能造成破门.问：在这一时间段内，对方球员有几次挑射破门的机会？简述理由.

查看试题解析

四、（本题8分）

20. 先化简，再求值： $x^{2} - [x^{2} - 2 x y + 3 (x y - \frac{1}{3} y^{2})]$ 其中 $x = - 4$ ， $y = - \frac{1}{2}$ .

查看试题解析

五、（本题共9分）

21. 如图，在边长都为a的正方形内分别排列着一些大小相等的圆：

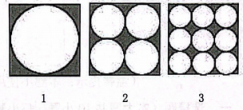(1)、根据图中的规律，第4个正方形内圆的个数是，第n个正方形内圆的个数是.

(2)、如果把正方形内除去圆的部分都涂上阴影.
①用含a的代数式分别表示第1个正方形中、第3个正方形中阴影部分的面积（结果保留 $π$ ）；
②若 $a = 10$ ，请直接写出第2023个正方形中阴影部分的面积 ▲ （结果保留 $π$ ）.

查看试题解析

六、（本题共10分）

22. 在数轴上，表示数1的点记为O，我们把到O点距离相等的两个不同点M和N，称为基准1的对称点.例如：图1中，点M表示数-1，点N表示数3，它们与表示数1的点O的距离都是2个单位长度，点M与点N互为基准1的对称点.
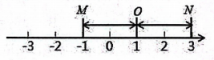
图1

(1)、已知点A表示数a，点B表示数b，点A与点B互为基准1的对称点.
①若 $a = 4$ ，则b=；
②用含a的式子表示b，则b=；

(2)、对点A进行如下操作：先把点A表示的数乘以 $\frac{5}{3}$ ，再把所得数对应的点沿着数轴向左移动2个单位长度得到点B.若点A与点B互为基准1的对称点，求点A表示的数.

查看试题解析

七、附加题（5分，计入总分，但满分不超过100分）

23. 设 $x_{1} ， x_{2} ， x_{3} ， ⋯ ， x_{10}$ 为自然数，且 $x_{1} < x_{2} < ⋯ < x_{10}$ ， $x_{1} + x_{2} + x_{3} + ⋯ + x_{10} = 2023$ ，则 $x_{8} + x_{9} + x_{10}$ 的最小值是.

查看试题解析

1	2	3	4	5
+0.031	+0.017	+0.023	-0.021	-0.015