人教版初中数学2023-2024学年九年级上学期期末模拟卷（二）

试卷更新日期：2023-12-11 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，在正方形网格中，将 $△ M N P$ 绕某一点旋转某一角度得到 $△ M_{1} N_{1} P_{1}$ ，则旋转中心是（）

A、点A B、点B C、点C D、点D

查看试题解析
3. 已知关于x的一元二次方程 $x^{2} + b x + c = 0$ 有一个非零实数根c ，则 $b + c$ 的值为（）

A、1 B、-1 C、0 D、2

查看试题解析
4. 掷一枚质地均匀的标有1，2，3，4，5，6六个数字的立方体骰子，骰子停止后，出现可能性最大的是（）

A、大于4的点 B、小于4的点数 C、大于5的点数 D、小于5的点数

查看试题解析
5. 下列事件中，属于不可能事件的是（）

A、经过红绿灯路口，遇到绿灯 B、班里的两名同学，他们的生日是同一天 C、射击运动员射击一次，命中靶心 D、一个只装有白球和红球的袋中摸球，摸出黄球

查看试题解析
6. 如图中的五角星图案，绕着它的中心O旋转n°后，能与自身重合，则n的值至少是（　　）

A、60 B、72 C、120 D、144

查看试题解析
7. 雷达通过无线电的方法发现目标并测定它们的空间位置，因此雷达被称为“无线电定位”．现有一款监测半径为5km的雷达，监测点的分布情况如图，如果将雷达装置设在P点，每一个小格的边长为1km ，那么能被雷达监测到的最远点为（　　）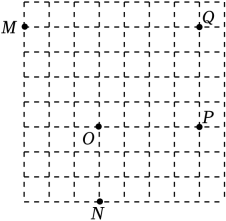

A、M点 B、N点 C、P点 D、Q点

查看试题解析
8. 如图，在⊙O中，直径AB⊥CD，若∠COB=65°，则∠BAD的度数是（）

A、25° B、65° C、32.5° D、50°

查看试题解析
9. 如图，在 $⊙ A$ 中，弦BC，ED所对的圆心角分别是 $∠ B A C ， ∠ E A D$ ， $∠ B A C$ 与 $∠ E A D$ 互补，已知 $B C = 8 ， D E = 6$ .当 $B C / / D E$ 时，弦BC与DE之间的距离等于（）.

A、7 B、1或7 C、 $\frac{\sqrt{41} + \sqrt{34}}{2}$ D、 $\frac{\sqrt{41} + \sqrt{34}}{2}$ 或 $\frac{\sqrt{41} - \sqrt{34}}{2}$

查看试题解析
10. 如图，已知抛物线 $y = - x^{2} + p x + q$ 的对称轴为 $x = - 3$ ，过其顶点 $M$ 的一条直线 $y = k x + b$ 与该抛物线的另一个交点为 $N (- 1 ， 1) .$ 要在坐标轴上找一点 $P$ ，使得 $△ P M N$ 的周长最小，则点 $P$ 的坐标为（）

A、 $(0 ， 2)$ B、 $(\frac{4}{3} ， 0)$ C、 $(0 ， 2)$ 或 $(\frac{4}{3} ， 0)$ D、以上都不正确

查看试题解析

二、填空题

11. 关于x的一元二次方程kx²+3x-1=0有实数根，则k的取值范围是

查看试题解析
12. 抛掷一枚均匀的骰子(骰子各个面上的点数为1~6)两次，称为一次试验．汇总全班同学的试验次数共计800次，其中一次试验中两次骰子的点数和为6的频数达120次．据此可以估计：抛掷一枚均匀的骰子两次，其点数和为6这一事件发生的概率为.

查看试题解析
13. 如图1是某地公园的一座抛物线型拱桥，按如图2所示建立坐标系，得到函数 $y = - \frac{1}{16} x^{2}$ ，在正常水位时水面宽 $A B = 24$ 米，当水位上升5米时，则水面宽 $C D =$ 米．
图1 图2

查看试题解析
14. 如图，将△ABC绕点A逆时针旋转到△ADE的位置，B、D、C在一条直线上．若∠B＝70°，则∠CAE的大小为．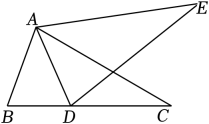

查看试题解析
15. 如图，MN是⊙O的直径，MN=2．点A在⊙O上，∠AMN=30°，B为 $\overset{⌢}{A N}$ 的中点，P为直径MN上一动点，则PA+PB的最小值为

查看试题解析

三、作图题

16. 在平面直角坐标系 $x O y$ 中，二次函数 $y = a x^{2} + b x + 3 (a \neq 0)$ 的图象经过点 $A (- 1，4)$ ， $B (1，0)$ ．

(1)、求二次函数的解析式；

(2)、画出二次函数的图象；

(3)、当 $y > 0$ 时，直接写出 $x$ 的取值范围．

查看试题解析

四、解答题

17. 某公园要在一个足够大的草地上规划出一个矩形草坪ABCD，矩形草坪ABCD的长AD为a米，宽AB为b米，并计划在草坪ABCD上种植两条宽均为x米的两条互相垂直的花带（阴影部分），且两条花带与矩形的边分别平行，余下的四块矩形草坪改为种植景观树．

(1)、已知 $a = 26$ ， $b = 15$ ，且种植景观树的总面积为312平方米，每条花带的宽为多少米？

(2)、若 $a ： b = 2 ： 1$ ，每条花带的宽均为2米，且种植景观树的总面积为312平方米，求a，b的值．

查看试题解析
18. 第31届世界大学生夏季运动会将于2023年7月28日至8月8日在成都举行，大熊猫是成都最具特色的对外传播标识物和“品牌图腾”，是天府之国享有极高知名度的个性名片．此次成都大运会吉祥物“蓉宝”（如图1）便是以熊猫基地真实的大熊猫“芝麻”为原型创作的．某商店销售“蓉宝”的公仔毛绒玩具，进价为30元/件，经市场调查发现：该商品的月销售量y（件）与销售价x（元/件）之间的关系如图2所示．
图1 图2

(1)、求y关于x的函数解析式；

(2)、由于某种原因，该商品进价提高了a元/件（ $a > 0$ ），如果规定该玩具售价不超过40元/件，该商品在今后的销售中，月销售量与销售价仍然满足（1）中的函数关系，若该商品的月销售最大利润是2400元，求a的值．

查看试题解析
19. 我校开展“阳光体育活动”，决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动，为了了解学生对这五项活动的喜爱情况，随机调查了一些学生（每名学生必选且只能选择这五项活动中的一种）．根据以下统计图提供的信息，请解答下列问题：

(1)、本次被调查的学生有 ▲ 名；补全条形统计图；

(2)、扇形统计图中“排球”对应的扇形的圆心角度数是；

(3)、学校准备推荐甲、乙、丙、丁四名同学中的2名参加全市中学生篮球比赛，请用列表法或画树状图法分析甲和乙同学同时被选中的概率．

查看试题解析
20. 如图，在Rt△ABC中，∠C= 90°，将△ABC绕着点B逆时针旋转得到△FBE，点C，A的对应点分别为E，F，点F落在BA上，连接AF．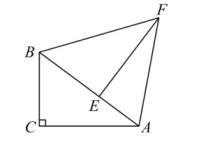

(1)、若∠BAC=40°，则∠AFE的度数为

(2)、若AC=8，BC=6，求AF的长．

查看试题解析
21. 如图，等腰 $△ A B C$ 内接于 $⊙ O$ ， AC的垂直平分线交边BC于点E ，交 $⊙ O$ 于F ，垂足为D ，连接AF并延长交BC的延长线于点P ．

(1)、求证： $∠ C A P = \frac{1}{2} ∠ B$ ；

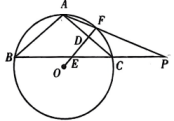(2)、若 $E B = C P$ ，求 $∠ B A C$ 的度数．

查看试题解析
22.
在平面直角坐标系中，抛物线y＝ax²+bx+c（a≠0）经过点A（-1，0）和B（0，3），其顶点的横坐标为1．

(1)、求抛物线的表达式．

(2)、若直线x＝m与x轴交于点N，在第一象限内与抛物线交于点M，当m取何值时，使得AN+MN有最大值，并求出最大值．

(3)、若点P为抛物线y＝ax²+bx+c（a≠0）的对称轴上一动点，将抛物线向左平移1个单位长度后，Q为平移后抛物线上一动点．在（2）的条件下求得的点M，是否能与A、P、Q构成平行四边形？若能构成，求出Q点坐标；若不能构成，请说明理由．

查看试题解析