人教版初中数学2023-2024学年九年级上学期期末模拟卷(一)
试卷更新日期:2023-12-11 类型:期末考试
一、选择题
-
1. 下列是一元二次方程的是( )A、x+y=1 B、x2+2=0 C、2x2-y=1 D、2. 如表,是某同学求代数式ax2+bx (a,b为常数)的值的情况.根据表格中数据,可知方程ax2+bx=6的根是( )
x
……
-2
-1
0
1
2
3
……
ax2+bx
……
6
2
0
0
2
6
……
A、x1=-2,x2=3 B、x1=-2,x2=-3 C、x1=2,x2=3 D、x1=2,x2=-33. 关于二次函数y= (x-2)2+3的最大值或最小值,下列叙述正确的是( )A、当x=2时,y有最大值3 B、当x=-2时,y有最大值3 C、当x=2时,y有最小值3 D、当x=-2时,y有最小值34. 已知点(-1,y1),(3,y2),( , y3)都在函数y=x2+2x+4的图象上,则y1、y2、y3的大小关系是( )A、y1>y2>y3 B、y2>y1>y3 C、y2>y3>y1 D、y3>y1>y25. 将分别标有“孔”、“孟”、“乏”、“乡”汉字的四个小球装在一个不透明的口集中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀.随机摸出一球,不放回;再随机摸出一球.两次摸出的球上的汉字能组成“孔孟”的概率是( )A、 B、 C、 D、6. 下列四个品牌图标中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,把△ABC绕C点顺时针旋转35°,得到△A'B'C,A'B'交AC于点D, 若∠A'DC=90°,则∠A的度数( )
7. 如图,把△ABC绕C点顺时针旋转35°,得到△A'B'C,A'B'交AC于点D, 若∠A'DC=90°,则∠A的度数( )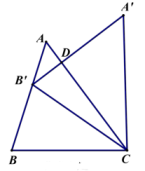 A、35° B、75° C、55° D、65°8. 如图,是绕点顺时针旋转得到的,延长与相交于点、若 , , , 则的度数为( )
A、35° B、75° C、55° D、65°8. 如图,是绕点顺时针旋转得到的,延长与相交于点、若 , , , 则的度数为( )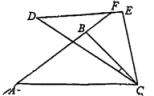 A、 B、 C、 D、9. 如图,AB为的直径,点D是的中点,过点D作于点E , 延长DE交于点F . 若 , , 则的直径长为( )
A、 B、 C、 D、9. 如图,AB为的直径,点D是的中点,过点D作于点E , 延长DE交于点F . 若 , , 则的直径长为( ) A、 B、8 C、10 D、10. 如图,点A、B分别在x轴、y轴上();以为直径的圆经过原点O,C是的中点,连结 , . 下列结论:①;②;③若 , , 则的面积等于5;④若 , 则点C的坐标是 , 其中正确的结论有( )
A、 B、8 C、10 D、10. 如图,点A、B分别在x轴、y轴上();以为直径的圆经过原点O,C是的中点,连结 , . 下列结论:①;②;③若 , , 则的面积等于5;④若 , 则点C的坐标是 , 其中正确的结论有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 关于x的方程的一个根为-2,则另一个根是 .12. 如图显示了爪计算札模拟随机投掷一枚图钉的实验结果.随着试验次数的增加,“钉尖向上”的频率总在某个数字附近,显示出一定的稳定性,可以估计“钉尖向上”的概率是 (精确到 0.001)
 13. 如图,在平面直角坐标系中,点B坐标(8,4), 连接OB, 将OB绕点O逆时针旋转90°,得到OB',则点B′的坐标为 .
13. 如图,在平面直角坐标系中,点B坐标(8,4), 连接OB, 将OB绕点O逆时针旋转90°,得到OB',则点B′的坐标为 . 14. 《九章算术》是中国传统数学重要的著作之一,其中第九卷《勾股》中记载了一个“圆材埋壁”的问题:“今有圆材,埋在壁中,不知大小.以锯锯之、深一寸,锯道长一尺,问径几何?”用几何语言表达为:如图,AB是⊙O的直径,弦CD⊥AB于点E , EB=1寸,CD=10寸,则直径AB长为 寸.
14. 《九章算术》是中国传统数学重要的著作之一,其中第九卷《勾股》中记载了一个“圆材埋壁”的问题:“今有圆材,埋在壁中,不知大小.以锯锯之、深一寸,锯道长一尺,问径几何?”用几何语言表达为:如图,AB是⊙O的直径,弦CD⊥AB于点E , EB=1寸,CD=10寸,则直径AB长为 寸.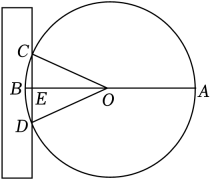 15. 二次函数的大致图象如图所示,顶点坐标为 , 下列结论:
15. 二次函数的大致图象如图所示,顶点坐标为 , 下列结论:
;
;
;
若方程有两个根和 , 且 , 则;
若方程有四个根,则这四个根的和为 .
其中正确的结论为 .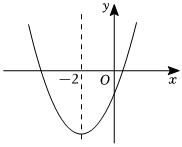
三、作图题
-
16. 如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△OAB的顶点都在格点上,已知点A(-4,-2),B(-2,-6).

⑴将△OAB向右平移4个单位长度得到△O1A1B1 , 请画出△O1A1B1;
⑵将△OAB绕点O顺时针旋转90°,画出所得的△OA2B2 .四、解答题
-
17. 为培养学生正确的劳动价值观和良好的劳动品质.某校为此规划出矩形苗圃ABCD . 苗圃的一面靠墙(墙最大可用长度为15米)另三边用木栏围成,中间也用垂直于墙的木栏隔开分成面积相等的两个区域,并在如图所示的两处各留1米宽的门(门不用木栏),修建所用木栏总长28米,设矩形ABCD的一边CD长为x米.
 (1)、矩形ABCD的面积为72m2 , 求出AB的长.(2)、矩形ABCD的面积能否为80m2 , 若能,请求出AB的长;若不能,请说明理由.18. 某公司推出一种环保日用品,年初投放市场后,公司经历了从亏损到盈利的过程.如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:
(1)、矩形ABCD的面积为72m2 , 求出AB的长.(2)、矩形ABCD的面积能否为80m2 , 若能,请求出AB的长;若不能,请说明理由.18. 某公司推出一种环保日用品,年初投放市场后,公司经历了从亏损到盈利的过程.如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题: (1)、求累积利润s(万元)与时间t(月)之间的函数表达式.(2)、估计8月末公司累积利润是多少万元;(3)、按这一经营状况,截止几月末公司累积利润可达到30万元?19. 九年级某班一次抽奖活动的规则如下:所印50张奖券中,一等奖2张,二等奖10张,三等奖25张,其余为安慰奖,每人限抽一张.(1)、第一个抽奖者抽得一等奖的概率是多少?抽得一等奖或二等奖的概率是多少?(2)、若第一个抽奖者抽走了一张三等奖,则第二个抽奖者抽得一等奖的概率是多少?抽得二等奖或三等奖的概率是多少?20. 如图,在中, , 将逆时针旋转后得到 , C点落在BD边上, , 求的度数.
(1)、求累积利润s(万元)与时间t(月)之间的函数表达式.(2)、估计8月末公司累积利润是多少万元;(3)、按这一经营状况,截止几月末公司累积利润可达到30万元?19. 九年级某班一次抽奖活动的规则如下:所印50张奖券中,一等奖2张,二等奖10张,三等奖25张,其余为安慰奖,每人限抽一张.(1)、第一个抽奖者抽得一等奖的概率是多少?抽得一等奖或二等奖的概率是多少?(2)、若第一个抽奖者抽走了一张三等奖,则第二个抽奖者抽得一等奖的概率是多少?抽得二等奖或三等奖的概率是多少?20. 如图,在中, , 将逆时针旋转后得到 , C点落在BD边上, , 求的度数. 21. 正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
21. 正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM. (1)、求证:EF=FM;(2)、当AE=2时,求EF的长.22. 如图,抛物线与x轴交于点A和点B,与y轴交于点C.
(1)、求证:EF=FM;(2)、当AE=2时,求EF的长.22. 如图,抛物线与x轴交于点A和点B,与y轴交于点C. (1)、求出A、B、C三点的坐标;(2)、将抛物线图像x轴上方部分沿x轴向下翻折,保留抛物线与x轴的交点和x轴下方图像,得到的新图像记作M,图像M与直线恒有四个交点,从左到右四个交点依次记为D,E,F,G.若以为直径作圆,该圆记作图像N.
(1)、求出A、B、C三点的坐标;(2)、将抛物线图像x轴上方部分沿x轴向下翻折,保留抛物线与x轴的交点和x轴下方图像,得到的新图像记作M,图像M与直线恒有四个交点,从左到右四个交点依次记为D,E,F,G.若以为直径作圆,该圆记作图像N.①在图像M上找一点P,使得的面积为3,求出点P的坐标;
②当图像N与x轴相离时,直接写出t的取值范围.
23. 在平面直角坐标系中,给出如下定义:将图形绕直线上某一点顺时针旋转 , 得到图形 , 再将图形关于直线对称,得到图形此时称图形为图形关于点的“二次变换图形”已知点 . (1)、若点 , 直接写出点关于点的“二次变换图形”的坐标;(2)、若点关于点的“二次变换图形”与点重合,求点的坐标;(3)、若点 , 半径为已知长度为的线段 , 其关于点的“二次变换图形”上的任意一点都在上或内,直接写出点的纵坐标的取值范围.
(1)、若点 , 直接写出点关于点的“二次变换图形”的坐标;(2)、若点关于点的“二次变换图形”与点重合,求点的坐标;(3)、若点 , 半径为已知长度为的线段 , 其关于点的“二次变换图形”上的任意一点都在上或内,直接写出点的纵坐标的取值范围.
-