人教版初中数学2023-2024学年八年级上学期期末模拟卷(三)
试卷更新日期:2023-12-11 类型:期末考试
一、选择题
-
1. 下列长度的三条线段能组成三角形的是( )A、5,6,10 B、1,2,3 C、2,3,6 D、3,4,72. 如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为 , 提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是( )
 A、AB,BC,CA B、AB,BC, C、AB,AC, D、 , , BC3. 使分式有意义的条件是( )A、 B、 C、 D、4. 下列因式分解正确的是( )A、 B、 C、 D、5. 如图,正方形ABCD和长方形AEFG的面积相等,且四边形BEFH也是正方形,欧几里得在《几何原本》中利用该图得到了:BH2=CH×GH.设AB=a,CH=b.若ab=5,则图中阴影部分的周长是 ( )
A、AB,BC,CA B、AB,BC, C、AB,AC, D、 , , BC3. 使分式有意义的条件是( )A、 B、 C、 D、4. 下列因式分解正确的是( )A、 B、 C、 D、5. 如图,正方形ABCD和长方形AEFG的面积相等,且四边形BEFH也是正方形,欧几里得在《几何原本》中利用该图得到了:BH2=CH×GH.设AB=a,CH=b.若ab=5,则图中阴影部分的周长是 ( )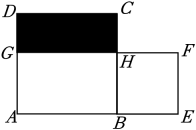 A、6 B、8 C、10 D、206. 世界文化遗产“三孔”景区已经完成5G基站布设,“孔夫子家”自此有了5G网络.5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输500兆数据,5G网络比4G网络快45秒,求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输x兆数据,依题意,可列方程是( )A、 B、 C、 D、7. 下列图形中,不是轴对称图形的是( )A、
A、6 B、8 C、10 D、206. 世界文化遗产“三孔”景区已经完成5G基站布设,“孔夫子家”自此有了5G网络.5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输500兆数据,5G网络比4G网络快45秒,求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输x兆数据,依题意,可列方程是( )A、 B、 C、 D、7. 下列图形中,不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪的三个顶点的距离相等,凉亭的位置应选在 ( )
8. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪的三个顶点的距离相等,凉亭的位置应选在 ( )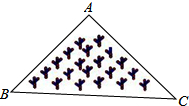 A、△ABC三边的垂直平分线的交点 B、△ABC的三条中线的交点 C、△ABC三条角平分线的交点 D、△ABC三条高所在直线的交点9. 如图,在中, , 的垂直平分线交于点D,交于点E,若 , 则( )
A、△ABC三边的垂直平分线的交点 B、△ABC的三条中线的交点 C、△ABC三条角平分线的交点 D、△ABC三条高所在直线的交点9. 如图,在中, , 的垂直平分线交于点D,交于点E,若 , 则( ) A、 B、 C、 D、10. 如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=3BF;⑤S△ADB=2S△BDF , 其中正确的结论共有( )
A、 B、 C、 D、10. 如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=3BF;⑤S△ADB=2S△BDF , 其中正确的结论共有( )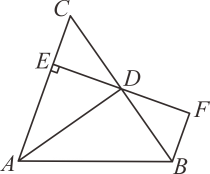 A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
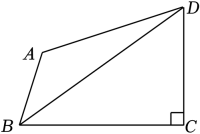
11. 在△ABC中,∠A=35°,∠B=65°,则∠C的度数是.12. 若am= 4,a2m+n= 128,则an=13. 如图,四边形ABCD中,∠BCD=90°,∠ABD=∠DBC,AB=5,DC=6,则△ABD的面积为 .
 14. 如图,已知AE=AD,请你添加一个条件: , 使△ABE≌△ACD.(图形中不再增加其他字母)
14. 如图,已知AE=AD,请你添加一个条件: , 使△ABE≌△ACD.(图形中不再增加其他字母) 15. 如图,△ABC中,AB=AC, 分别以A、B为圆心, 以适当的长为半径作弧,两弧分别交于E、F,D为BC的中点,M为直线EF上任意一点, 若BC=4, △ABC的面积为10,则BM+MD的最小值是 .
15. 如图,△ABC中,AB=AC, 分别以A、B为圆心, 以适当的长为半径作弧,两弧分别交于E、F,D为BC的中点,M为直线EF上任意一点, 若BC=4, △ABC的面积为10,则BM+MD的最小值是 .
三、计算题
-
16. 先化简,再求值: , 其中 , .
四、解答题
-
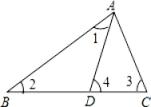
17. 如图,在△ABC中,∠1=∠2,∠3=∠4,∠BAC=54°,求∠DAC的度数.
 18. 如图,在△ABC中,AB=AC,BD是AC边上的高线.
18. 如图,在△ABC中,AB=AC,BD是AC边上的高线. (1)、若∠C=2∠A ,求∠DBC的度数.(2)、设∠A=α,求∠DBC的度数.(用含α的代数式表示)19. 如图,AB=CD,AF=CE,BE⊥AC于E,DF⊥AC于F.求证:
(1)、若∠C=2∠A ,求∠DBC的度数.(2)、设∠A=α,求∠DBC的度数.(用含α的代数式表示)19. 如图,AB=CD,AF=CE,BE⊥AC于E,DF⊥AC于F.求证: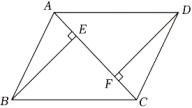 (1)、△ABE≌△CDF.(2)、AD∥BC.20. 小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
(1)、△ABE≌△CDF.(2)、AD∥BC.20. 小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题: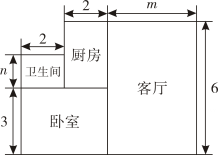 (1)、用含m , n的代数式表示地面的总面积;(2)、已知n=1.5,且客厅面积是卫生间面积的8倍,如果铺1平方米地面的平均费用为200元,那么小王铺地砖的总费用为多少元?21. 某镇道路改造工程,预计由甲、乙两工程队合作20天可完成,甲队单独施工完成的天数是乙队单独施工完成天数的2倍.(1)、求甲、乙两队单独完成此项工程各需要多少天;(2)、若甲队独做n天后,再由甲、乙两队合作q天可完成此项工程,则n , q之间的关系式为;(3)、为了加快工程进度,甲、乙两队各自提高工作效率,提高后甲队的工作效率是 , 乙队的工作效率是甲队工作效率的m(m为常数)倍.若提高效率后两队合作10天完成整个工程的 , 求甲队提高后的工作效率是提高前工作效率的几倍(用含m的代数式表示).22. 已知,在中, , .
(1)、用含m , n的代数式表示地面的总面积;(2)、已知n=1.5,且客厅面积是卫生间面积的8倍,如果铺1平方米地面的平均费用为200元,那么小王铺地砖的总费用为多少元?21. 某镇道路改造工程,预计由甲、乙两工程队合作20天可完成,甲队单独施工完成的天数是乙队单独施工完成天数的2倍.(1)、求甲、乙两队单独完成此项工程各需要多少天;(2)、若甲队独做n天后,再由甲、乙两队合作q天可完成此项工程,则n , q之间的关系式为;(3)、为了加快工程进度,甲、乙两队各自提高工作效率,提高后甲队的工作效率是 , 乙队的工作效率是甲队工作效率的m(m为常数)倍.若提高效率后两队合作10天完成整个工程的 , 求甲队提高后的工作效率是提高前工作效率的几倍(用含m的代数式表示).22. 已知,在中, , .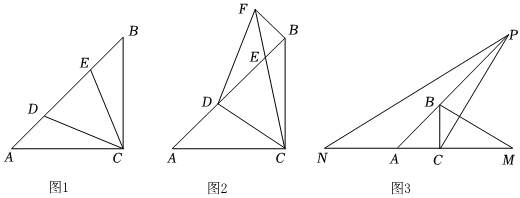 (1)、如图 , 点、点分别是线段上两点,连接、 , 若 , 且 , 求的度数;(2)、如图 , 点、点分别是线段上两点,连接、 , 过点作交延长线于 , 连接 , 若 , 求证:;(3)、如图 , 为射线上一点,为射线上一点,且始终满足 , 过点作的垂线交的延长线于点 , 连接 , 猜想:、、之间的数量关系并证明你的结论.
(1)、如图 , 点、点分别是线段上两点,连接、 , 若 , 且 , 求的度数;(2)、如图 , 点、点分别是线段上两点,连接、 , 过点作交延长线于 , 连接 , 若 , 求证:;(3)、如图 , 为射线上一点,为射线上一点,且始终满足 , 过点作的垂线交的延长线于点 , 连接 , 猜想:、、之间的数量关系并证明你的结论.
-