人教版初中数学2023-2024学年八年级上学期期末模拟卷（二）

试卷更新日期：2023-12-11 类型：期末考试

进入出卷网下载

一、选择题

1. 下列等式成立的是（）

A、 $\frac{1}{a} + \frac{2}{a} = \frac{3}{2 a}$ B、 $\frac{a}{a - 1} + \frac{1}{1 - a} = \frac{a + 1}{a - 1}$ C、 $\frac{x}{x + 1} + \frac{1}{x + 1} = 1$ D、 $\frac{1}{{(m - 2)}^{2}} - \frac{m - 1}{{(m - 2)}^{2}} = \frac{m - 2}{{(m - 2)}^{2}}$

查看试题解析
2. 分解因式 $4 + a^{2} - 4 a$ 正确的是（）

A、 ${(2 - a)}^{2}$ B、 $4 (1 - a) + a^{2}$ C、 $(2 - a) (2 + a)$ D、 ${(2 + a)}^{2}$

查看试题解析
3. （） $\times a b = 2 a b^{2}$ ，则括号内应填的单项式是（）

A、2 B、2a C、2b D、4b

查看试题解析
4. 下面是一位同学用三根木棒拼成的图形，其中符合三角形概念的是（）

A、 B、 C、 D、

查看试题解析
5. 三角形三个内角中，锐角最多可以有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
6. 如图所示，在 $△ A B C$ 中，点 $E$ 在AD上，且点 $E$ 是 $△ A B C$ 的重心，若 $S_{△ A B C} =$ 36，则 $S_{△ D E C}$ 等于（）.

A、3 B、4 C、6 D、9

查看试题解析
7. 如图，直线 $A B / / E F ， C$ 是直线AB上一点， $D$ 是直线AB外一点，若 $∠ B C D = 95^{°} ， ∠ C D E = 25^{°}$ ，则 $∠ D E F$ 的度数是（）

A、 $110^{°}$ B、 $115^{°}$ C、 $120^{°}$ D、 $125^{°}$

查看试题解析
8. 如图，△ABC≌△EDC，BC⊥CD，点A，D，E在同一条直线上，∠ACB＝25°，则∠ADC的度数是（）

A、45° B、60° C、75° D、70°

查看试题解析
9. 如图，下列四个条件： ①BC＝B′C；②AC＝A′C；③∠A′CA＝∠B′CB；④AB＝A′B′.从中任取三个为条件，余下的一个为结论，则最多可以构成正确的结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
10. 如图，在△ABC中，∠ABC＝45°，F是高AD和BE的交点，CD＝4，则线段DF的长为（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

11. 已知关于 $a$ 的多项式 $a^{2} + a + m$ ( $m$ 为常数)可以用完全平方公式直接述行因式分解，则 $m$ 的值为.

查看试题解析
12. 将 $f = \frac{u v}{u + v}$ 变形为已知f，u，且 $f \neq u$ ，则 $v$ 的公式为.

查看试题解析
13. 在△ABC中，AB=AC，∠B=50°，D是BC的中点，连结AD，则∠DAC=.

查看试题解析
14. 如图，点B，E，C，F在同一条直线上，AB=DE，BE=CF．请你添加一个条件：（只需添加一个），使△ABC≌△DEF．

查看试题解析
15. 如图，已知四边形ABCD中，AC平分∠BAD，CE⊥AB于点E，且AE＝ $\frac{1}{2}$ (AB＋AD)，若∠D＝115°，则∠B＝．

查看试题解析

三、计算题

16. 因式分解：

(1)、 $36 - x^{2}$ ；

(2)、 $- 2 a^{3} + 12 a^{2} - 18 a$ .

查看试题解析
17. 先化简再求值： $\frac{x^{2} - 4}{x^{2} + 4 x + 4}$ ÷（ $\frac{2 x - 4}{x + 2}$ ﹣x＋2），其中x可在﹣2，0，3三个数中任选一个合适的数.

查看试题解析

四、作图题

18. 如图，在4×4的正方形方格中，阴影部分是涂黑5个小正方形所形成的图案.将方格内空白的两个小正方形涂黑，使得到的新图案成为一个轴对称图形，请在下面的图中至少画出四个不同的方案，并画出对称轴.

查看试题解析

五、解答题

19. 已知：如图，在△ABC中，AB=AC，AM是BC边，上的中线，点N在AM上．求证：NB=NC．

查看试题解析
20. 已知：如图，AB与CD相交于点O，∠A=∠D，CO=BO．求证：AO=DO．

查看试题解析
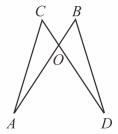21. 为打好“蓝天、碧水、净土”三大保卫战，某县政府决定将县城附近乡村的烧煤取暖全部改制为集中供热.“永盛”工程队承包了该项工程10000m的总管道铺设任务，若该工程队施工效率比原计划提高25%，就可以比原计划提前20天完成任务。请解答下列问题：

(1)、“永盛”工程队提高施工效率后平均每天铺设管道多少m？

(2)、在（1）的基础上为了缩短工期，在管道铺设了20天后，该工程队经研究决定，余下的管道铺设任务要在50天内（含50天）完成，求该工程队平均每天至少再多铺设多少m？

查看试题解析
22. 已知：如图，在△ABC中，∠B=60°，D、E分别为AB、BC上的点，且AE、CD交于点F．若AE、CD为△ABC的角平分线．

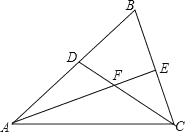(1)、求证：∠AFC=120°；

(2)、若AD=6，CE=4，求AC的长？

查看试题解析
23. 已知AM∥CN，点B为平面内一点，AB⊥BC于B．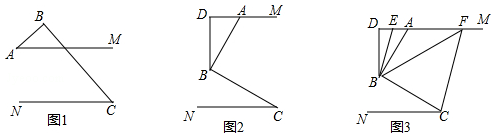

(1)、如图1，直接写出∠A和∠C之间的数量关系；

(2)、如图2，过点B作BD⊥AM于点D，求证：∠ABD=∠C；

(3)、如图3，在（2）问的条件下，点E、F在DM上，连接BE、BF、CF，BF平分∠DBC，BE平分∠ABD，若∠FCB+∠NCF=180°，∠BFC=3∠DBE，求∠EBC的度数．

查看试题解析