人教版初中数学2023-2024学年八年级上学期期末模拟卷（一）

试卷更新日期：2023-12-11 类型：期末考试

进入出卷网下载

一、选择题

1. 长度为8，3，x的三条线段构成三角形，则x的值可能是（）

A、3 B、7 C、5 D、12

查看试题解析
2. 如图，在△ABC中，∠A=35°，∠C=45°，则与∠ABC相邻的外角的度数是（）

A、35° B、45° C、80° D、100°

查看试题解析
3. 工人师傅常用角尺平分一个任意角．做法如下：如图，∠AOB是一个任意角，在边OA ， OB上分别取OM＝ON ，移动角尺，使角尺两边相同的刻度分别与点M ， N正合，过角尺顶点C连OC ．可知△OMC≌△ONC ， OC便是∠AOB的平分线．则△OMC≌△ONC的理由是（）

A、SSS B、SAS C、AAS D、HL

查看试题解析
4. 如图，最适合用“HL”定理判定Rt△ABC和Rt△DEF全等的条件是（）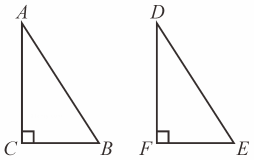

A、AC=DF，BC=EF． B、∠A=∠D，AB=DE． C、AC=DF，AB=DE． D、∠B=∠E，BC= EF．

查看试题解析
5. 如图，在△ABC中，AB=AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别是E，F．下列结论中，不正确的是（）

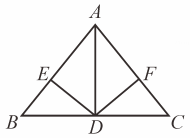A、DA平分∠EDF B、AE=AF C、AD上任一点P到AB，AC的距离相等 D、AB，AC上的点到AD的距离相等

查看试题解析
6. 一个等腰三角形的底边长为5，一条腰上的中线把其周长分成的两部分的差为3，则这个等腰三角形的腰长为（）

A、2 B、8 C、2或8 D、10

查看试题解析
7. 若□×3ab =- 6a⁵b³ ，则□内应填的单项式是（）

A、2a⁴b² B、-2a⁴b² C、-2a⁵b D、2a³b

查看试题解析
8. 已知（x+m）（x-5）=x²-3x+k．则k，m的值分别是（）

A、k=10，m=2 B、k=10，m=-2 C、k=-10，m=-2 D、k=-10，m=2

查看试题解析
9. 师傅和徒弟两人每小时一共做40个零件，在相同的时间内，师傅做了300个零件，徒弟做了100个零件．师傅每小时做了多少个零件？若设师傅每小时做了x个零件，则可列方程为（　　）

A、 $\frac{300}{x} = \frac{100}{40 - x}$ B、 $\frac{300}{40 - x} = \frac{100}{x}$ C、 $\frac{300}{x} = \frac{100}{x - 40}$ D、 $\frac{300}{x - 40} = \frac{100}{x}$

查看试题解析
10. 如图， $∠ A B C = ∠ A C B$ ， $A D$ 、 $B D$ 、 $C D$ 分别平分 $△ A B C$ 的外角 $∠ E A C$ 、内角 $∠ A B C$ 、外角 $∠ A C F .$ 以下结论：

$① A D / / B C$ ； $② ∠ B D C = \frac{1}{2} ∠ B A C$ ；

$③ ∠ A D C = 90 ° - ∠ A B D$ ； $④ B D$ 平分 $∠ A D C$ ．

其中正确的结论有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析

二、填空题

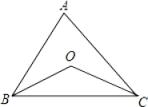
11. 若（a-2023）⁰=1，则a的取值范围是

查看试题解析
12. 已知 $x + y = - 5$ ， $x - y = - 4$ ，则 $x^{2} - y^{2}$ 的值是．

查看试题解析
13. 如图，BO、CO分别平分∠ABC和∠ACB，∠A＝70°，则∠BOC＝°．

查看试题解析
14. 如图，△ABC是等边三角形，AD∥BC，CD⊥AD．若AD =2cm，则AB=cm．

查看试题解析
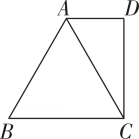15. 如图，已知AD=DE，AB=BE，若∠A=75°，则∠CED =度．

查看试题解析
16. 如图， $△ A B C$ 中， $∠ A B C$ 、 $∠ F C A$ 的角平分线 $B P$ 、 $C P$ 交于点 $P$ ，延长 $B A$ 、 $B C$ ， $P M ⊥ B E$ 于 $M$ ， $P N ⊥ B F$ 于 $N$ ，则下列结论：① $A P$ 平分 $∠ E A C$ ；② $∠ A B C + 2 ∠ A P C = 180 °$ ；③ $∠ B A C = 2 ∠ B P C$ ；④ $S_{△ P A C} = S_{△ M A P} + S_{△ N C P}$ ．其中正确结论序号是．

查看试题解析

三、计算题

17. 计算：

(1)、（2a²）³+（-3a³）²；

(2)、（x+3y）（x-y）．

查看试题解析
18. 先化简（ $\frac{3}{a + 1}$ -a+1）÷ $\frac{a^{2} - 4 a + 4}{a + 1}$ ，然后从-2≤a≤2的范围内选择一个合适的整数作为a的值代入求值．

查看试题解析

四、作图题

19. 如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A坐标为（2，4）．

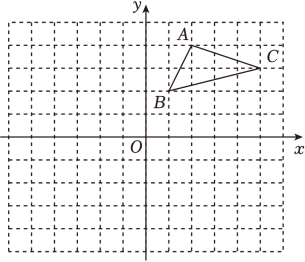(1)、画出△ABC关于x轴对称的△A₁B₁C₁；

(2)、若把△ABC向左平移2个单位后的三角形为△A₂B₂C₂ ，求△A₂B₂C₂的顶点坐标．

查看试题解析

五、解答题

20. 节能又环保的油电混合动力汽车，既可以用油做动力行驶，也可以用电做动力行驶，某品牌油电混合动力汽车从甲地行驶到乙地，若完全用油做动力行驶，则费用为80元；若完全用电做动力行驶，则费用为30元，已知汽车行驶中每千米用油费用比用电费用多0.5元.

(1)、求汽车行驶中每千米用电费用是多少元？甲、乙两地的距离是多少千米？

(2)、若汽车从甲地到乙地采用油电混合动力行驶，要使行驶总费用不超过60元，求至少需要用电行驶多少千米？

查看试题解析
21. 当我们利用两种不同的方法计算同一图形的面积时，可以得到一个等式，例如，由图1，可得等式：（a+2b）（a+b）＝a²+3ab+2b² ．

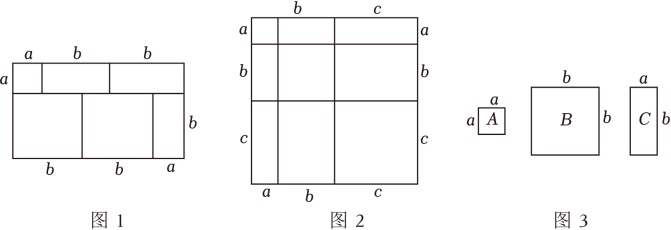(1)、由图2，可得等式：．

(2)、利用（1）中所得到的结论，解决下面的问题：已知a+b+c＝12，ab+bc+ac＝28，求a²+b²+c²的值．

查看试题解析
22. 如图，在△ABC中，∠B＝75°，∠C＝25°，AD是高，AE是∠BAC的平分线。
求∠BAE和∠EAD的度数．

查看试题解析
23. 已知：如图，点E，F在BC上，BE=CF，∠A=∠D，∠B=∠C，AF与DE交于点O．求证：AB=DC．

查看试题解析
24. 等腰 $R t △ A C B$ ， $∠ A C B = 9 0^{∘}$ ， $A C = B C$ ，点 $A$ ， $C$ 分别在 $x$ 轴， $y$ 轴的正半轴上．

(1)、如图 $1$ ，求证： $∠ B C O = ∠ C A O$ ．

(2)、如图2，若 $O A = 10$ ， $O C = 4$ ，求 $B$ 点的坐标．

(3)、如图3，点 $C (0 ， 4)$ ， $Q$ ， $A$ 两点均在 $x$ 轴上，且 $S_{△ C Q A} = 36$ ，分别以 $A C$ ， $C Q$ 为腰在第一、第二象限作等腰 $R t △ C A N$ 、等腰 $R t △ Q C M$ ，连接 $M N$ 交 $y$ 轴于 $P$ 点， $O P$ 的长度是否发生变化？若不变，求出 $O P$ 的值；若变化，求 $O P$ 的取值范围．

查看试题解析