2023-2024学年广东省(人教版)七年级(上)数学期末模拟卷(一)
试卷更新日期:2023-12-11 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 2022年10月16日,中国共产党第二十次全国代表大会在北京人民大会堂开幕.开幕式中一组组亮眼的数据,展示了新时代十年发展的新成就.其中,国内生产总值从540000亿元增长到1140000亿元.把“1140000”用科学记数法表示为( )A、 B、 C、 D、2. 在数轴上,把表示的点沿着数轴移动7个单位长度得到的点所表示的数是( )A、5 B、 C、 D、5或3. 下列等式变形中,错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则4. 下列几何体中,三棱锥是( )A、
 B、
B、 C、
C、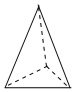 D、
D、 5. 在数轴上表示a,b两数的点如图所示,则下列判断正确的是( )
5. 在数轴上表示a,b两数的点如图所示,则下列判断正确的是( )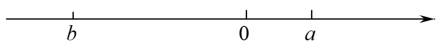 A、 B、 C、 D、6. 如图所示,某同学的家在处,他想尽快赶到附近处搭顺风车.他选择第②条路线,用几何知识解释其道理正确的是( )
A、 B、 C、 D、6. 如图所示,某同学的家在处,他想尽快赶到附近处搭顺风车.他选择第②条路线,用几何知识解释其道理正确的是( ) A、两点确定一条直线 B、两点之间,线段最短 C、垂线段最短 D、经过一点有无数条直线7. 下列各组中,属于同类项的是( )A、和 B、和 C、和 D、和8. 如图,一副三角板(直角顶点重合)摆放在桌面上,若 , 则( )
A、两点确定一条直线 B、两点之间,线段最短 C、垂线段最短 D、经过一点有无数条直线7. 下列各组中,属于同类项的是( )A、和 B、和 C、和 D、和8. 如图,一副三角板(直角顶点重合)摆放在桌面上,若 , 则( ) A、30° B、45° C、50° D、60°9. 下面的平面图形均由六个边长相等的小正方形组成,经过折叠不能围成正方体的是( )A、
A、30° B、45° C、50° D、60°9. 下面的平面图形均由六个边长相等的小正方形组成,经过折叠不能围成正方体的是( )A、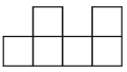 B、
B、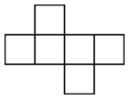 C、
C、 D、
D、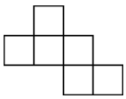 10. 某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在“六·一”儿童节举行文具优惠售卖活动,铅笔按原价打八折出售,圆珠笔按原价打九折出售,结果两种笔共卖出60支,卖得金额87元.若设铅笔卖出支,则依题意可列得的一元一次方程为( )A、 B、 C、 D、
10. 某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在“六·一”儿童节举行文具优惠售卖活动,铅笔按原价打八折出售,圆珠笔按原价打九折出售,结果两种笔共卖出60支,卖得金额87元.若设铅笔卖出支,则依题意可列得的一元一次方程为( )A、 B、 C、 D、二、填空题(每题3分,共15分)
-
11. 如果向西走30米记作米,那么米表示 .12. 多项式的次数是 .13. 是方程的解.(请填写所有符合条件方程的序号)
①;②;③;④ .
14. 截一个几何体,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.如图,截面平行于底面,则这个几何体的截面是 . 15. 将一张长方形的纸按照如图所示折叠后,点C、D两点分别落在点C'、D'处,若EA平分∠D'EF,则∠DEF= 。
15. 将一张长方形的纸按照如图所示折叠后,点C、D两点分别落在点C'、D'处,若EA平分∠D'EF,则∠DEF= 。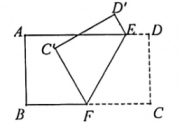
三、解答题(共8题,共75分)
-
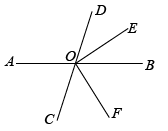
16. 计算:(1)、(2)、17. 定义一种新运算:对任意有理数 , 都有 , 例如: .(1)、求的值;(2)、先化简,再求值: , 其中 , .18. 如图,已知直线 , 相交于点 , 平分 , 平分 , , 求的度数.
 19. 已知长方形的长为4cm、宽为3cm , 将其绕它的一边所在的直线旋转一周,得到一个几何体,
19. 已知长方形的长为4cm、宽为3cm , 将其绕它的一边所在的直线旋转一周,得到一个几何体, (1)、求此几何体的表面积.(结果保留π)(2)、求此几何体的体积;(结果保留π)20. 如图, , , , 四点在同一条直线上.
(1)、求此几何体的表面积.(结果保留π)(2)、求此几何体的体积;(结果保留π)20. 如图, , , , 四点在同一条直线上.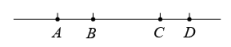 (1)、若 ,
(1)、若 ,①比较线段的大小:;(填“>”“=”或“<”)
②若 , 且 , 则的长为cm;
(2)、若线段被点 , 分成了三部分,且的中点和的中点之间的距离是20cm,求的长.21. 某市为保障供水及道路安全,自来水有限公司排查地下管线密集区,决定改造一段已使用多年面临老化的自来水管,这项翻新工程如果由甲工程队单独改造需要12天,由乙工程队单独改造需要24天.现要求甲、乙两个工程队一起合作完成这项翻新工程,但由于工作调动的原因,该项工程完工时,乙工程队中途共离开了3天,问这项工程一共用了多少天?22. 某超市第一次以4450元购进甲、乙两种商品,其中乙商品的件数是甲商品件数的2倍多15件,甲、乙两种商品的进价和售价如下表:(注:利润=售价-进价)甲
乙
进价(元/件)
20
30
售价(元/件)
25
40
(1)、该超市第一次购进甲、乙两种商品各多少件?(2)、该超市第二次以第一次的进价又购进甲、乙两种商品,其中乙商品的件数不变,甲商品的件数是第一次的2倍;乙商品按原价销售,甲商品打折销售,第二次两种商品都销售完以后获得的总利润与第一次获得的总利润一样,求第二次甲商品是按原价打几折销售?23. (阅读材料)我们知道,“角”是由一条射线绕着它的端点旋转而成的图形.射线在单位时间内以固定的角度绕其端点沿某一方向旋转,经过不同的旋转时间都会形成不同的角.
在行程问题中,我们知道:运动路程=运动速度×运动时间;
类似的,在旋转问题中,我们规定:旋转角度=旋转角速度×旋转时间.
例如(如图),射线OM从射线OA出发,以每秒10°的旋转速度(称为“旋转角速度”)绕点逆时针旋转.旋转1秒得旋转角度∠MOA=10°×1=10°,旋转2秒得旋转角度∠MOA=10°×2=20°,……,旋转t秒得旋转角度∠MOA=10°×t=(10t)°.
(问题解决)
如图1,射线OA上有两点M、N.将射线OM以每秒10°的旋转角速度绕点O逆时针旋转(OM最多旋转9秒);射线OM旋转3秒后,射线ON开始以每秒20°的旋转角速度绕点O逆时针旋转,如图2所示.设射线ON旋转时间为t秒.
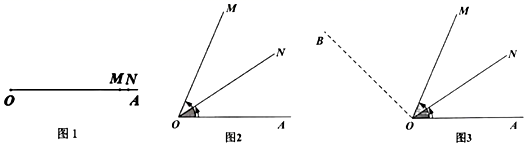 (1)、当t=2时,∠MON=°;(2)、当∠MON=20°时,求t的值;(3)、如图3,OM、ON总是在某个角∠AOB的内部旋转,且当ON为∠AOB的三等分线时,OM恰好平分∠AOB,求∠AOB的度数.
(1)、当t=2时,∠MON=°;(2)、当∠MON=20°时,求t的值;(3)、如图3,OM、ON总是在某个角∠AOB的内部旋转,且当ON为∠AOB的三等分线时,OM恰好平分∠AOB,求∠AOB的度数.