广东省佛山市南海区重点中学2023-2024学年高一上学期数学12月月考试卷

试卷更新日期：2023-12-11 类型：月考试卷

进入出卷网下载

一、单项选择题

1. 已知集合 $M = {5 ， a^{2} - 3 a + 5}$ ， $N = {1 ， 3}$ ，若 $M ∩ N \neq \emptyset$ ，则实数 $a$ 的值为（）

A、1 B、2 C、1或2 D、4

查看试题解析
2. 当 $0 < a < 1$ 时，在同一坐标系中，函数 $y = a^{- x}$ 与 $y = l o g_{a} x$ 的图象可以是（）

A、 B、 C、 D、

查看试题解析
3. 下列函数中，既是奇函数又是区间 $(0 ， + \infty)$ 上的增函数的是（）

A、 $y = x^{3}$ B、 $y = x^{- 1}$ C、 $y = x^{\frac{1}{2}}$ D、 $y = 2^{x}$

查看试题解析
4. 函数 $f (x) = l n x - \frac{2}{x}$ 的零点所在的大致区间是（）

A、 $(1 ， 2)$ B、 $(2 ， 3)$ C、 $(3 ， 4)$ D、 $(e ， 3)$

查看试题解析
5. 已知函数 $f (x) = (m^{2} - m - 1) x^{m^{2} + m - 1}$ 是幂函数，且在 $(0 ， + \infty)$ 上是减函数，则实数 $m$ 的值是（）.

A、 $- 1$ 或2 B、2 C、 $- 1$ D、1

查看试题解析
6. 设 $a = 2^{0.3} ， b = {(\frac{1}{2})}^{- 0.5} ， c = \ln 2$ ，则（）

A、 $c < b < a$ B、 $c < a < b$ C、 $a < b < c$ D、 $b < a < c$

查看试题解析
7. 若偶函数 $f (x)$ 在 $(- \infty ， - 1)$ 上单调递减，在 $(- 1 ， 0)$ 单调递增，且 $f (0) = 2$ ， $f (2) = 0$ ，则函数 $f (x)$ 的零点个数是（）

A、1 B、2 C、3 D、4

查看试题解析
8. 某化工厂生产一种溶质，按市场要求，杂质含量不能超过0.01%.若该溶质的半成品含杂质1%，且每过滤一次杂质含量减少为原来的 $\frac{1}{3}$ ，则要使产品达到市场要求，该溶质的半成品至少应过滤（）

A、5次 B、6次 C、7次 D、8次

查看试题解析

二、多项选择题

9. 集合 $M = {(x ， y) | x + y \leq 1 ， x \in N ； y \in N}$ 中的元素有（）

A、 $(0 ， 0)$ B、 $(0 ， 1)$ C、 $(1 ， 0)$ D、 $(2 ， - 1)$

查看试题解析
10. 若 $a$ ， $b$ 是任意正实数，且 $a > b$ ，则下列不等式成立的有（）

A、 $a^{2} > b^{2}$ B、 $\frac{b}{a} < 1$ C、 $l g (a - b) > 0$ D、 ${(\frac{1}{3})}^{a} < {(\frac{1}{3})}^{b}$

查看试题解析
11. 已知函数 $f (x)$ 是 $R$ 上的奇函数，且当 $x \geq 0$ 时， $f (x) = x^{2} + x + a - 2$ ，则（）

A、 $a = 2$ B、 $f (x)$ 是减函数 C、 $f (x)$ 只有一个零点 D、 $f (- 3) = - 12$

查看试题解析
12. 如图，某池塘里的浮萍面积 $y$ (单位： $m^{2}$ )与时间 $t$ (单位：月)的关系式为 $y = k a^{t}$ ( $k \in R$ ，且 $k \neq 0$ ； $a > 0$ 且 $a \neq 1$ ).则下列说法正确的是（）

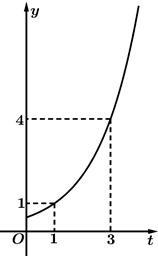A、浮萍每月增加的面积都相等 B、第6个月时，浮萍的面积会超过 $30 m^{2}$ C、浮萍每月的增长率为1 D、若浮萍面积蔓延到 $4 m^{2}$ ， $6 m^{2}$ ， $9 m^{2}$ 所经过的时间分别为 $t_{1}$ ， $t_{2}$ ， $t_{3}$ ，则 $t_{1} + t_{3} = 2 t_{2}$

查看试题解析

三、填空题

13. 函数 $f (x) = {\begin{cases} x^{2} - 4 ， x \leq 0 \\ l n x + x - 2 ， x > 0 \end{cases}$ 的零点个数是.

查看试题解析
14. 函数 $y = f (x)$ 与函数 $g (x) = a^{x}$ 互为反函数，且 $y = f (x)$ 图像经过点 $(10 ， 1)$ ，则 $f (100) =$ .

查看试题解析
15. 若函数 $f (x) = \frac{k}{x}$ 在区间 $[2 ， 4]$ 上的最小值为5，则 $k$ 的值为.

查看试题解析
16. 已知 $f (x) = {\begin{array}{l} - 4 x + 2 a ， x \geq 1 \\ x^{2} - a x + 4 ， x < 1 \end{array}$ 是 $R$ 上的减函数，则实数 $a$ 的取值范围为.

查看试题解析

四、解答题

17. 已知集合 $A = {x | a - 1 < x < 2 a + 3}$ ， $B = {x | - 7 \leq x \leq 4}$ .

(1)、若 $a = 2$ ，求 $A ∪ B$ ；

(2)、若 $A ∩ (∁_{R} B) = A$ ，求实数 $a$ 的取值范围.

查看试题解析
18. 已知函数 $f (x) = {\begin{array}{l} a x + 1 ， x \leq 0 \\ | l o g_{2} x | ， x > 0 \end{array}$ .

(1)、当 $a = - 2$ 时，在给定的坐标系中作出函数 $f (x)$ 的图象，并写出它的单调递减区间；

(2)、若 $a \geq 0$ ，且 $f (x_{0}) = 2$ ，求实数 $x_{0}$ .

查看试题解析
19. 已知函数 $f (x) = \log_{a} (3 + 2 x) ， g (x) = \log_{a} (3 - 2 x)$ ( $a > 0$ ，且 $a \neq 1$ ).

(1)、判断函数 $f (x) - g (x)$ 的奇偶性，并予以证明；

(2)、求使 $f (x) - g (x) > 0$ 的x的取值范围.

查看试题解析
20. 已知函数 $f (x) = a - \frac{3}{2^{x} + 1}$ .

(1)、判断函数 $f (x)$ 的单调性，并证明你的结论；

(2)、若方程 $f (x) = 0$ 在 $(- 1 ， 1)$ 有解，求实数 $a$ 的取值范围.

查看试题解析
21. 为践行“绿水青山，就是金山银山”，我省决定净化闽江上游水域的水质.省环保局于2018年年底在闽江上游水域投入一些蒲草，这些蒲草在水中的蔓延速度越来越快，2019年2月底测得蒲草覆盖面积为 $36 m^{2}$ ， 2019年3月底测得蒲草覆盖面积为 $48 m^{2}$ .设经过 $x$ 个月蒲草覆盖面积为 $y$ （单位： $m^{2}$ ）， $x$ ， $y$ 的关系有以下两个函数模型 $y = k a^{x}$ （ $k > 0$ ， $a > 1$ ）与 $y = m x^{2} + n$ （ $m > 0$ ）可供选择.

(1)、分别求出两个函数模型的解析式；

(2)、若2018年年底测得蒲草覆盖面积为 $20 m^{2}$ ，从上述两个函数模型中选择更合适的一个模型，试估算至少到哪一年的几月底蒲草覆盖面积能超过 $810 m^{2}$ ？（参考数据： $l g 2 \approx 0.30$ ， $l g 3 \approx 0.48$ ）

查看试题解析
22. 已知函数 $f (x) = a x^{2} + b x$ （ $a$ ， $b$ 是常数且 $a \neq 0$ ）的一个零点是2，且方程 $f (x) = x$ 有两相等实根.

(1)、求 $f (x)$ 的解析式；

(2)、问是否存在实数 $m$ ， $n$ （ $m < n$ ）使 $f (x)$ 的定义域和值域分别为 $[m ， n]$ 和 $[2 m ， 2 n]$ ，如果存在，求出 $m$ ， $n$ 的值；如果不存在，说明理由.（艺术班选做）

查看试题解析