湖北省荆州市松滋市重点中学2023-2024学年高三上学期数学12月月考试卷
试卷更新日期:2023-12-11 类型:月考试卷
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 已知数列的前项和为 , 数列是递增数列是的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件2. 若存在实数x∈[2,4],使x2-2x+5-m<0成立,则m的取值范围为( )
A、(13,+∞) B、(5,+∞) C、(4,+∞) D、(-∞,13)3. 函数的图象大致为( )A、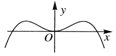 B、
B、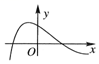 C、
C、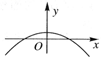 D、
D、 4. 已知函数在上有且仅有个零点,则的取值范围是( )A、 B、 C、 D、5. 已知平面向量 , 满足 , , 并且当时,取得最小值,则( )A、 B、 C、 D、6. 设等差数列的前项和为 , 数列的前和为 , 已知 , , , 若 , 则正整数的值为( )A、 B、 C、 D、7. 三棱锥中,平面 , 若 , , 则该三棱锥体积的最大值为( )A、 B、 C、 D、8. 设 , , , 则( )A、 B、 C、 D、
4. 已知函数在上有且仅有个零点,则的取值范围是( )A、 B、 C、 D、5. 已知平面向量 , 满足 , , 并且当时,取得最小值,则( )A、 B、 C、 D、6. 设等差数列的前项和为 , 数列的前和为 , 已知 , , , 若 , 则正整数的值为( )A、 B、 C、 D、7. 三棱锥中,平面 , 若 , , 则该三棱锥体积的最大值为( )A、 B、 C、 D、8. 设 , , , 则( )A、 B、 C、 D、二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
-
9. 已知函数 , 则下列结论正确的是( )A、在上单调递增 B、有极小值 C、在点处的切线斜率为 D、为奇函数10. 如图,在棱长为的正方体中,下列结论正确的是( )
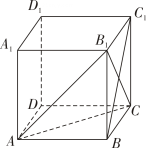 A、异面直线与所成的角为 B、直线与平面所成角为 C、二面角的正切值为 D、四面体的外接球的体积为11. 在锐角中,角 , , 所对的边为 , , , 若 , 且 , 则的可能取值为( )A、 B、 C、 D、12. 已知点 , , , , 则下列结论正确的为( )A、当时, B、当时,点在直线上 C、当时, D、当时,在方向上的投影向量的模为
A、异面直线与所成的角为 B、直线与平面所成角为 C、二面角的正切值为 D、四面体的外接球的体积为11. 在锐角中,角 , , 所对的边为 , , , 若 , 且 , 则的可能取值为( )A、 B、 C、 D、12. 已知点 , , , , 则下列结论正确的为( )A、当时, B、当时,点在直线上 C、当时, D、当时,在方向上的投影向量的模为三、填空题(本大题共4小题,共20.0分)
-
13. 复数满足 , 则 .14. 已知函数 ,实数 满足 ,且 ,若 在 的最大值为2,则 .15. 数学王子高斯在小时候计算时,他是这样计算的: , 共有组,故和为 , 事实上,高斯发现并利用了等差数列的对称性若函数图象关于对称, , 则 .16. 已知函数对于任意 , 都有 , 且当时,若函数恰有个零点,则的取值范围是 .
四、解答题(本大题共6小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 已知函数 .(1)、若 , 且 , 求的值;(2)、若对任意的 , 不等式恒成立,求实数的最小值.18. 已知数列的前项和为 , , , .(1)、求;(2)、求 .19. 如图,圆台下底面圆的直径为 , 是圆上异于的点,且 , 为上底面圆的一条直径,是边长为的等边三角形, .
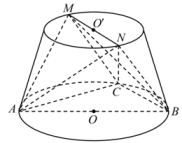 (1)、证明:平面;(2)、求平面和平面夹角的余弦值.20. 为了增强学生的国防意识,某中学组织了一次国防知识竞赛,高一和高二两个年级学生参加知识竞赛,
(1)、证明:平面;(2)、求平面和平面夹角的余弦值.20. 为了增强学生的国防意识,某中学组织了一次国防知识竞赛,高一和高二两个年级学生参加知识竞赛,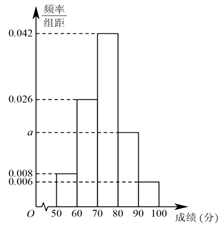 (1)、两个年级各派名学生参加国防知识初赛,成绩均在区间上,现将成绩制成如图所示频率分布直方图每组均包括左端点,最后一组包括右端点 , 请估计学生的成绩的平均分同一组中的数据用该组区间的中点值为代表;(2)、两个年级各派一位学生代表参加国防知识决赛,决赛的规则如下:决赛一共五轮,在每一轮中,两位学生各回答一个题目,累计答对题目数量多者胜;若五轮答满,分数持平,则并列为冠军;如果在答满轮前,其中一方答对题目数量已经多于另一方答满轮题最多可能答对的题目数量,则不需再答题,譬如:第轮结束时,双方答对题目数量比为: , 则不需再答第轮了;设高一年级的学生代表甲答对比赛题目的概率是 , 高二年级的学生代表乙答对比赛题目的概率是 , 每轮答题比赛中,双方答对与否互不影响,各轮结果也互不影响.
(1)、两个年级各派名学生参加国防知识初赛,成绩均在区间上,现将成绩制成如图所示频率分布直方图每组均包括左端点,最后一组包括右端点 , 请估计学生的成绩的平均分同一组中的数据用该组区间的中点值为代表;(2)、两个年级各派一位学生代表参加国防知识决赛,决赛的规则如下:决赛一共五轮,在每一轮中,两位学生各回答一个题目,累计答对题目数量多者胜;若五轮答满,分数持平,则并列为冠军;如果在答满轮前,其中一方答对题目数量已经多于另一方答满轮题最多可能答对的题目数量,则不需再答题,譬如:第轮结束时,双方答对题目数量比为: , 则不需再答第轮了;设高一年级的学生代表甲答对比赛题目的概率是 , 高二年级的学生代表乙答对比赛题目的概率是 , 每轮答题比赛中,双方答对与否互不影响,各轮结果也互不影响.在一次赛前训练中,学生代表甲同学答了轮题,记为他答对题目的数量,求的分布列及数学期望.
求在第轮结束时,学生代表甲答对道题并刚好胜出的概率.