四川省南部名校2023-2024学年高三上册数学第四次月考试卷
试卷更新日期:2023-12-11 类型:月考试卷
一、单项选择题.本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求.
-
1. 若隻合 , , 则( )A、 B、 C、 D、2. 复数的共轭复数是( )A、 B、 C、 D、3. 已知向量 , 若 , 则( )A、25 B、5 C、 D、4. 若 , , , 则( )A、 B、 C、 D、5. 在△ABC中,“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件6. 记 为等差数列 的前n项和.已知 ,则A、 B、 C、 D、7. 基本再生数与世代间隔是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:描述累计感染病例数随时间(单位:天)的变化规律,指数增长率与 , 近似满足 . 有学者基于已有数据估计出=3.07,=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(参考数据:ln2≈0.69)( )A、1.5天 B、2天 C、2.5天 D、3.5天8. 函数在区间上的图象为( )A、
 B、
B、 C、
C、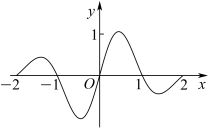 D、
D、 9. 已知函数在区间上是增函数,且在区间上存在唯一的使得 , 则的取值不可能为( )A、 B、 C、 D、110. 已知函数 的值域为 ,那么实数 的取值范围是( )A、 B、[-1,2) C、(0,2) D、11. 在中,内角A , B , C的对边分别为a , b , c , 若 , , 则的外接圆的面积为( )A、 B、 C、 D、12. 已知函数 , ,若 , ,则 的最大值为( )A、 B、 C、 D、
9. 已知函数在区间上是增函数,且在区间上存在唯一的使得 , 则的取值不可能为( )A、 B、 C、 D、110. 已知函数 的值域为 ,那么实数 的取值范围是( )A、 B、[-1,2) C、(0,2) D、11. 在中,内角A , B , C的对边分别为a , b , c , 若 , , 则的外接圆的面积为( )A、 B、 C、 D、12. 已知函数 , ,若 , ,则 的最大值为( )A、 B、 C、 D、二、填空题:本题共4小题,每小题5分,共20分.
-
13. 已知函数 , 则.14. 在平行四边形 中, 点E满足且 , 则实数 .15. 已知函数在区间上的最小值为 .16. 已知函数 , 函数 , 则下列结论正确的是 .
①若有3个不同的零点,则a的取值范围是
②若有4个不同的零点,则a的取值范围是
③若有4个不同的零点 , 则
④若有4个不同的零点 , 则的取值范围是
三、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
17. 等比数列 的各项均为正数,且 .(1)、求数列 的通项公式;(2)、设bn=log3a1+log3a2+…+log3an , 求数列 的前 项和 .18. 已知函数 .(1)、求函数的最小正周期和单调递减区间;(2)、若将函数的图象向右平移个单位长度,再将图象上所有点的横坐标伸长到原来的两倍(纵坐标不变),得到函数的图象,求函数在区间上的值域.19. 已知函数.(1)、若 , 求的极值.(2)、若方程在区间上有解,求实数的取值范围.20. 在① , ② , ③的面积为这三个条件中任选一个,补充在下面的问题中,并加以解答.
已知的内角 , , 所对的边分别为 , , , 且 ▲ .
(1)、求角;(2)、若为的中点,且 , , 求 , 的值.