2023-2024学年初中数学八年级上册 1.3.2 零次幂和负整数指数幂同步分层训练培优卷(湘教版)

试卷更新日期：2023-12-11 类型：同步测试

进入出卷网下载

一、选择题

1. 若 $a = - {0.1}^{2}$ ， $b = - 3^{2}$ ， $c = {(- \frac{1}{3})}^{- 2}$ ， $d = {(- \frac{1}{3})}^{0}$ ，则它们的大小关系是（）

A、 $a < d < c < b$ B、 $a < b < d < c$ C、 $b < a < d < c$ D、 $c < d < a < b$

查看试题解析
2. 定义：如果 $a^{x} = N (a > 0 ， a \neq 1)$ ，那么x叫做以a为底N的对数，记作 $x = l o g_{a} N$ ．例如：因为 $7^{2} = 49$ ，所以 $l o g_{7} 49 = 2$ ；因为 $5^{3} = 125$ ，所以 $l o g_{5} 125 = 3$ ．则下列说法正确的个数为（）
① $l o g_{6} 1 = 0$ ；② $l o g_{3} 2^{3} = 3 l o g_{3} 2$ ；③若 $l o g_{2} (3 - a) = l o g_{8} 27$ ，则 $a = 0$ ；④ $l o g_{2} x y = l o g_{2} x + l o g_{2} y (x > 0 ， y > 0)$ ．

A、4 B、3 C、2 D、1

查看试题解析
3. 下列运算正确的是（）

A、 ${(a^{2})}^{3} = a^{5}$ B、 $2 x^{- 1} = \frac{2}{x}$ C、 $a^{3} \cdot a^{4} = a^{12}$ D、 ${(x - y)}^{2} = x^{2} - y^{2}$

查看试题解析
4. 把下列各数代入 ${(x + 1)}^{x + 4} = 1$ 中，等式成立的有（），① $x = 0$ ；② $x = 1$ ；③ $x = - 1$ ；④ $x = - 2$ ；⑤ $x = - 4$ .

A、①②③ B、②③④ C、①②⑤ D、①④⑤

查看试题解析
5. 如果 $a = {(- 99)}^{0}$ ， $b = {(- 0.1)}^{- 1}$ ， $c = {(- \frac{5}{3})}^{- 2}$ ，那么a、b、c三数的大小（）

A、 $c < b < a$ B、 $b < a < c$ C、 $b < c < a$ D、 $a < b < c$

查看试题解析
6. 下列各数中，结果是2023的是（）

A、 $202 3^{0}$ B、 $| - 2023 |$ C、 $0 - (+ 2023)$ D、 $2023 \times (- 1)$

查看试题解析
7. 如图，约定：上方相邻两数之和等于这两数下方箭头共同指向的数．下列判断正确的是（）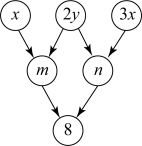

结论 Ⅰ ：若n的值为5，则y的值为1；

结论Ⅱ： $x + y$ 的值为定值；

结论Ⅲ：若 $x^{m - 3 n} = 1$ ，则y的值为4或1．

A、Ⅰ ，Ⅲ均对 B、Ⅱ对，Ⅲ错 C、Ⅱ错，Ⅲ对 D、Ⅰ ，Ⅱ均错

查看试题解析
8. 下列结论中： ①若 ${(1 - x)}^{x + 1} = 1$ ，则 $x = - 1$ ；②若 $a^{2} + b^{2} = 3 ， a - b = 1$ ，则 $(2 - a) (2 - b)$ 的值为 $5 - 2 \sqrt{5}$ ； ③若规定：当 $a b \neq 0$ 时， $a \otimes b = a + b - a b$ ，若 $a \otimes (4 - a) = 0$ ，则 $a = 2$ ；④若 $4^{x} = a ， 8^{y} = b$ ，则 $2^{4 x - 3 y}$ 可表示为 $\frac{2 a}{b}$ ； ⑤若 $(x + 1) (x - a)$ 的运算结果中不含 $x$ 的一次项，则 $a = 1$ . 其中正确的个数是（）

A、5 B、4 C、3 D、2

查看试题解析

二、填空题

9. 已知 $a = - (0.3)^{2} ， b = - 3^{- 2} ， c = {(- \frac{1}{3})}^{- 2} ， d = {(- \frac{1}{3})}^{0}$ ，则a、b、c、d的大小关系是．（用“>”号连接）

查看试题解析
10. 计算 $2^{5} \div 0 . 5^{- 4} - {(2 π - 6.28)}^{0}$ 的结果是.

查看试题解析
11. 若 ${(x + 4)}^{0}$ 有意义，则x的取值范围是．

查看试题解析
12. 若（t-3）^t-2=1，则t=.

查看试题解析
13. 若 ${(x + 3)}^{x - 3} = 1$ ，则 $x =$ 。

查看试题解析

三、解答题

14. 某种液体每升含有10¹²个细菌，某种杀菌剂1滴可以杀死10⁹个此种有害细菌，现在若要将3L这种液体中的有害细菌杀死，要用这种杀菌剂多少滴？
若10滴这种杀菌剂为10^-3L，要用多少升？

查看试题解析
15. 阅读材料：
（ 1 ）1的任何次幂都为1；

（ 2 ）-1的奇数次幂为-1；

（ 3 ）-1的偶数次幂为1；

（ 4 ）任何不等于零的数的零次幂为1.

请问当 $x$ 为何值时，代数式 ${(2 x + 3)}^{x + 2020}$ 的值为1.

查看试题解析

四、计算题

16. 计算：

(1)、（-1）²+ ${(\frac{1}{2})}^{- 1}$ -5-（2004-π）⁰

(2)、[（2x+y）²-y（y+4x）-8x]÷2x．

查看试题解析

五、综合题

17. 本学期我们学习了“有理数乘方”运算，知道乘方的结果叫做“幂”，下面介绍一种有关“幂”的新运算.
定义： $a^{m}$ 与 $a^{n}$ （ $a \neq 0$ ， $m$ ， $n$ 都是正整数）叫做同底数幂，同底数幂除法记作 $a^{m} \div a^{n}$ .

运算法则如下： $a^{m} \div a^{n} = {\begin{array}{l} 当 m > n 时， a^{m} \div a^{n} = a^{m - n} \\ 当 m = n 时， a^{m} \div a^{n} = 1 \\ 当 m < n 时， a^{m} \div a^{n} = \frac{1}{a^{n - m}} \end{array}$

根据“同底数幂除法”的运算法则，回答下列问题：

(1)、填空： ${(\frac{1}{3})}^{3} \div {(\frac{1}{3})}^{2} =$ ， $5^{2} \div 5^{4} =$ ；

(2)、如果 $x > 0$ ，且 $2^{x} \div 2^{2 x} = \frac{1}{8}$ ，求出 $x$ 的值；

(3)、如果 ${(x - 2)}^{2 x + 2} \div {(x - 2)}^{12} = 1$ ，则 $x =$ .

查看试题解析
18.

(1)、观察： ${(\frac{2}{3})}^{2} = \frac{2}{3} \times \frac{2}{3}$ ， ${(\frac{3}{2})}^{- 2} = \frac{1}{{(\frac{3}{2})}^{2}} = \frac{1}{\frac{3}{2}} \times \frac{1}{\frac{3}{2}} = \frac{2}{3} \times \frac{2}{3}$ ，我们发现 ${(\frac{2}{3})}^{2}$ ${(\frac{2}{3})}^{- 2}$ ；

(2)、仿照（1），请你通过计算，判断 ${(\frac{5}{4})}^{3}$ 与 ${(\frac{4}{5})}^{- 3}$ 之间的关系；

(3)、我们可以发现： ${(\frac{b}{a})}^{- m}$ （ $\frac{a}{b}$ ）^m（ab≠0）；

(4)、计算： ${(\frac{7}{15})}^{- 3} \cdot {(\frac{7}{5})}^{4}$ .

查看试题解析

2023-2024学年初中数学八年级上册 1.3.2 零次幂和负整数指数幂 同步分层训练培优卷(湘教版)

一、选择题

二、填空题

三、解答题

四、计算题

五、综合题

2023-2024学年初中数学八年级上册 1.3.2 零次幂和负整数指数幂同步分层训练培优卷(湘教版)