人教版初中数学2023-2024学年七年级上学期期末模拟卷（三）

试卷更新日期：2023-12-11 类型：期末考试

进入出卷网下载

一、选择题

1. 下列四个式子中，计算结果最小的是（）

A、（-3-2）2 B、（-3）×（-2）² C、-3²÷（-2）² D、-2³-3²

查看试题解析
2. 两数相乘，若积为正数，则这两个数（）

A、都是正数 B、都是负数 C、都是正数或都是负数 D、一个正数和一个负数

查看试题解析
3. 已知 $2 m - n = 2$ ， $m n = - 1$ ，则 $2 (m - n) - (m n - n) =$ （）

A、－5 B、5 C、－3 D、3

查看试题解析
4. 下面说法正确的是（）

A、－2x是单项式 B、 $\frac{3 a b}{5}$ 的系数是3 C、 $2 a b^{2}$ 次数是2 D、 $x^{2} + 2 x y$ 是四次多项式

查看试题解析
5. 下列去括号中，正确的是（）

A、 $a^{2} - (1 - 2 a) = a^{2} - 1 - 2 a$ B、 $a^{2} + (- 1 - 2 a) = a^{2} - 1 + 2 a$ C、 $a - [5 b - (2 c - 1)] = a - 5 b + 2 c - 1$ D、 $- (a + b) + (c - d) = - a - b - c + d$

查看试题解析
6. 下列各式是一元一次方程的是（）

A、 $2 x = 5 + 3 y$ B、 $y^{2} = y + 4$ C、 $3 x + 2 = 1 - x$ D、 $\frac{1}{x} = 2$

查看试题解析
7. 在足球比赛的前11场比赛中，某队仅负一场共积22分，按比赛规则，胜一场得三分，平一场得一分，负一场得0分，则该队共胜（）场

A、4 B、5 C、6 D、7

查看试题解析
8. 小何同学在做作业时，不小心将方程 $2 (x - 3) -$ ▊ $= x + 1$ 中一个常数污染了，在询问老师后，老师告诉他方程的解是 $x = 9$ ，请问这个被污染的常数▊是（）

A、4 B、3 C、2 D、1

查看试题解析
9. 如图是一个正方体的展开图，将它折叠成正方体后，“学”字对面的文字是（）

A、考 B、试 C、加 D、油

查看试题解析
10. 已知，点C在直线 AB 上， AC=a ， BC=b ，且 a≠b ，点 M是线段 AB 的中点，则线段 MC的长为（）

A、 $\frac{a + b}{2}$ B、 $\frac{a - b}{2}$ C、 $\frac{a + b}{2}$ 或 $\frac{a - b}{2}$ D、 $\frac{a + b}{2}$ 或 $\frac{| a - b |}{2}$

查看试题解析

二、填空题

11. 浙江省陆域面积为101 800平方千米，用科学记数法表示为平方千米．

查看试题解析
12. 将多项式5x²-4-3x³按x的降幂排列为：．

查看试题解析
13. 已知关于x的多项式4x²－3x＋5－2mx²－x＋1化简后不含x²项，则m的值是．

查看试题解析
14. 为迎接初一新生，47中清华分校对校园重新美化装修．现计划对教室墙体重新粉刷一遍（所有教室面积相同）．现有甲，乙两个装修队承担此项工作．已知甲队3天粉刷5个教室，结果其中有30平方米墙面未来得及粉刷；乙队5天粉刷7个教室外还多粉刷20平方米．已知甲队比乙队每天多粉刷10平方米，则每间教室的面积为平方米．

查看试题解析
15. 我们将圆形钟面的时针和分针看作是两条从圆心发出的射线，当时针和分针夹角180度时形成一条直线，这条直线刚好平分钟面，我们将这样的时刻称为“平衡时刻”，如图，6点整就是一个平衡时刻，请问从0时到24时共有个平衡时刻.

查看试题解析

三、计算题

16. 计算：

(1)、-11-7+6．

(2)、7.2+（-1.8）-（-0.8）．

(3)、 $- \frac{1}{3} + \frac{3}{4} - \frac{1}{6} - \frac{1}{2}$ .

查看试题解析
17. 化简

(1)、3x-2x²+5+3x²-2x

(2)、3（x²+y²）-（3y²-2x²）．

查看试题解析
18. 先化简，再求值：3x²y+2[2xy²-（xy+ $\frac{1}{2}$ x²y）]-xy² ，其中x＝2，y＝- $\frac{1}{2}$ ．

查看试题解析

四、解答题

19. 已知 $x = 2$ 是关于 $x$ 的方程 $m x = - 6$ 的解，求代数式 $m^{2} - (1 - 2 m) + 3 m$ 的值．

查看试题解析
20. 小亮在解方程3a-x=7时，由于粗心，错把-x看成了+x，结果解得x=-2．求a的值．

查看试题解析
21. 某工程甲单独完成要45天，乙单独完成要30天，若乙先单独干22天，剩下的由甲单独完成．问甲、乙一共用几天可以完成全部工作？

查看试题解析
22. 我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微：数形结合百般好，隔离分家万事休”．数学中，数和形是两个最主要的研究对象，它们之间有着十分密切的联系．数形结合是解决数学问题的重要思想方法．如图，数轴上A，B两点对应的有理数分别为-10和20，点P从点O出发，以每秒1个单位长度的速度沿数轴正方向匀速运动，点Q同时从点A出发，以每秒2个单位长度的速度沿数轴正方向匀速运动，设运动时间为t秒．

(1)、分别求当t＝2及t＝12时，对应的线段PQ的长度；

(2)、当PQ＝5时，求所有符合条件的t的值，并求出此时点Q所对应的数；

(3)、若点P一直沿数轴的正方向运动，点Q运动到点B时，立即改变运动方向，沿数轴的负方向运动，到达点A时，随即停止运动，在点Q的整个运动过程中，是否存在合适的t值，使得PQ=8？若存在，求出所有符合条件的t值，若不存在，请说明理由．

查看试题解析

五、综合题

23. 如图，已知同一平面内 $∠ A O B = 9 0^{∘}$ ， $∠ A O C = 6 0^{∘}$ ．

(1)、填空 $∠ B O C =$ ．

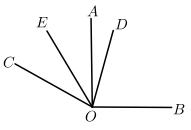(2)、如 $O D$ 平分 $∠ B O C$ ， $O E$ 平分 $∠ A O C$ ，直接写出 $∠ D O E$ 的度数为°．

(3)、试问在（2）的条件下，如果将题目中 $∠ A O C = 6 0^{∘}$ 改成 $∠ A O C = 2 α (α < 4 5^{∘})$ ，其他条件不变，你能求出 $∠ D O E$ 的度数吗？若能，请你写出求解过程；若不能，请说明理由．

查看试题解析