人教版初中数学2023-2024学年七年级上学期期末模拟卷（一）

试卷更新日期：2023-12-11 类型：期末考试

进入出卷网下载

一、选择题

1. 用科学记数法表示20 000，正确的是（）

A、2×10⁵ B、2×10⁴ C、0.2×10⁴ D、0.2×10⁵

查看试题解析
2. 下列计算正确的是（）

A、 $\frac{1}{3} - \frac{1}{3}$ ×4=0×4=0 B、4÷（-2）×（ $- \frac{1}{2}$ ）=4÷1=4 C、-3²-（-2）³=9-8=1 D、 $(- \frac{1}{4}) \div (\frac{1}{12} + \frac{1}{16}) = (- \frac{1}{4}) \div \frac{7}{48} = - \frac{12}{7}$

查看试题解析
3. 某天中午的气温是 $3 ℃$ ，记作 $+ 3 ℃$ ，晚上的气温是零下 $2 ℃$ ，则这天晚上的气温可记作（）

A、 $2 ℃$ B、 $1 ℃$ C、 $- 2 ℃$ D、 $- 1 ℃$

查看试题解析
4. 多项式2a²b-3mab²+ab的项数及次数分别是（）

A、3，4 B、3，3 C、3，2 D、2，3

查看试题解析
5. 如图，7张全等的小长方形纸片（既不重叠也无空隙）放置于矩形ABCD中，设小长方形的长为a ，宽为b（a＞b），若要求出两块黑色阴影部分的周长和，则只要测出下面哪个数据（）

A、a B、b C、a+b D、a-b

查看试题解析
6. 下列说法正确的是（）

A、如果ac＝bc ，那么a＝b B、如果a＝b ，那么a+2＝b-2 C、如果a＝b ，那么ac＝bc D、如果a²＝b² ，那么a＝b

查看试题解析
7. 一个两位数，十位上的数是 $1$ ，个位上的数是 $x$ ．把 $1$ 与 $x$ 对调，新两位数比原两位数大 $18$ ．根据题意列出的方程为（）．

A、 $10 x + 1 - 10 + x = 18$ B、 $10 x + 1 - (10 + x) = 18$ C、 $10 + x - 10 x + 1 = 18$ D、 $10 + x - (10 x + 1) = 18$

查看试题解析
8. 整式mx+2n的值随x的取值不同而不同，下表是当x取不同值时整式mx+2n对应的值，则关于x的方程-mx-2n=2的解为（）
x
-2
-1
0
1
2
mx+2n
2
0
-2
-4
-6

A、x=-1 B、x=-2 C、x=0 D、无法确定

查看试题解析
9. 如图是一个正方体的展开图，则该正方体可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图，在数轴上，点A表示1，现将点A沿数轴做如下移动：第一次将点A向左移动3个单位长度到达点A₁ ，第二次将点A向右移动6个单位长度到达点A₂ ，第三次将点A₂向左移动9个单位长度到达点A₃ ，按照这种移动规律移动下去，第n次移动到点A_n ，如果点A_n与原点的距离不小于20，那么n的最小值是（　　）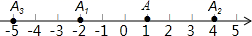

A、12 B、13 C、14 D、15

查看试题解析

二、填空题

11. 若单项式： $\frac{1}{2} a^{n - 2} b^{n - 1}$ 与 $\frac{1}{2} a^{3} b^{m + 3}$ 的和仍是单项式，则 $m + n =$ ．

查看试题解析
12. 已知关于 $x$ 的方程 $2 x + m - 8 = 0$ 的解是 $x = 3$ ，则 $m$ 的值为.

查看试题解析
13. 如图，在数轴上点A、B表示的数分别为-2、4，若点M从A点出发以每秒5个单位长度的速度沿数轴向右匀速运动，点N从B出发以每秒4个单位长度的速度沿数轴匀速运动，设点M、N同时出发，运动时间为t秒，经过秒后，M、N两点间的距离为12个单位长度．

查看试题解析
14. 同学们都知道，|5﹣（﹣2）|表示5与﹣2之差的绝对值，实际上也可以理解为5与﹣2两数在数轴上所对应的两点之间的距离，则使得|x﹣1|+|x+5|＝6这样的整数x有个．

查看试题解析
15. 如图，点 $A$ ， $B$ 是直线 $l$ 上的两点，点 $C$ ， $D$ 在直线 $l$ 上且点 $C$ 在点 $D$ 的左侧，点 $D$ 在点 $B$ 的右侧， $A C ： C B = 2 ： 1$ ， $B D ： A B = 3 ： 2$ .若 $C D = 11$ ，则 $A B =$ .

查看试题解析

三、解答题

16. 已知：A＝3a²+ab+2b ， B＝2a²-ab+b ．

(1)、求2A-3B的值；

(2)、若a²-3ab＝4，求A-2B的值．

查看试题解析
17. 某工业园区对甲、乙两个项目共投资2000万元甲项目的年收益率为5.4%，乙项目的年收益率为8.28%，投资一年后，该工业园区在这两个项目中共获得收益122.4万元．问：该工业园区对这两个项目各投资了多少万元？

查看试题解析
18. 某校组织七年级师生赴农场参加社会实践．如果单独租用45座客车若干辆，刚好坐满；如果单独租用60座客车，可少租1辆，且余15个座位．

(1)、求七年级师生参加社会实践的人数．

(2)、已知租45座的客车日租金为每辆2250元，60座的客车日租金为每辆2760元问：租哪种客车更合算？

(3)、你还有其他更省钱的租车方法吗？如果有，请给出方案，并说明理由．

查看试题解析
19. 如图，∠AOC=30°，∠BOC=80°，OC平分∠AOD．求∠BOD的度数．

查看试题解析
20. 数轴是学习有理数的一种重要工具，任何有理数都可以在数轴上表示，这样能够运用数形结合的方法解决一些问题，例如，两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示，如，在数轴上，有理数3与1对应的两点之间的距离为 $| 3 － 1 |$ =2，有理数5与-2对应的两点之间的距离为 $| 5 －（ - 2 ） |$ =7，有理数-8与-5对应的两点之间的距离为 $| - 8 －（ - 5 ） |$ =3.
如图，在数轴上有理数a对应的点为点A，有理数b对应的点为B，A，B两点之间的距离表示为 $| a － b |$ 或 $| b － a |$ ，记为 $| A B |$ = $| a － b |$ = $| b － a |$ .

(1)、解决问题：
数轴上有理数-10与3对应的两点之间的距离等于 ▲ ；数轴上有理数x与-5对应的两点之间的距离用含x的式子表示为 ▲ ；若数轴上有理数x与1对应的两点A，B之间的距离 $| A B |$ =6，则x等于 ▲ .

(2)、联系拓广：
如图，点M，N，P是数轴上的三点，点M表示的数为4，点N表示的数为-2，动点P表示的数为x.
①若点P在点M，N两点之间，则 $| P M |$ + $| P N |$ = ▲ ；若 $| P M |$ + $| P N |$ =10，则点P表示的数x为 ▲ ；由此可得：当 $| x + 3 |$ + $| x － 7 |$ 取最小值时，整数x的所有取值的和为 ▲ .
②当点P到点M的距离等于点P到点N的距离的2倍时，请直接写出x的值.

查看试题解析
21. 如图，OC在∠BOD内.

(1)、如果∠AOC和∠BOD都是直角.
①若∠BOC=60°，则∠AOD的度数是 ▲ ；
②猜想∠BOC与∠AOD的数量关系，并说明理由；

(2)、如果∠AOC=∠BOD=x°，∠AOD=y°，求∠BOC的度数.

查看试题解析

四、计算题

22. 计算：

(1)、0.6- $\frac{1}{4}$ -（-3.75）+ $\frac{2}{5}$

(2)、 $(- \frac{2}{5}) + (- 3 \frac{4}{7}) - 1.6 - (- \frac{11}{7})$

查看试题解析

x	-2	-1	0	1	2
mx+2n	2	0	-2	-4	-6