广东省深圳市2022-2023学年七年级上册数学期末仿真模拟卷

试卷更新日期：2023-12-11 类型：期末考试

进入出卷网下载

一、选择题

1. 神舟十五号载人飞船于2022年11月29日成功发射，载人飞船与空间站组合体对接后，在距离地球表面约430000米左右的轨道上运行.430000米用科学记数法表示是（）．

A、 $4.3 \times 1 0^{3}$ 米 B、 $4.3 \times 1 0^{5}$ 米 C、 $43 \times 1 0^{4}$ 米 D、 $0.43 \times 1 0^{4}$ 米

查看试题解析
2. 龙岗某校七年级（1）班期末考试数学的平均成绩是73分，小亮得了90分，记作+17分，若小英的成绩记作-3分，表示小英得了（）分．

A、76 B、73 C、77 D、70

查看试题解析
3. 如图，数轴上的三个点A、B、C表示的数分别是a、b、C，且|a|=|b|，AB=BC，则下列结论中①ab<0；②a=-b：③a+c>0；④3a+c=0中，正确的有（）个．

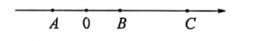A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列图形中，是棱柱表面展开图的是（）

A、 B、 C、 D、

查看试题解析
5. 单项式 $\frac{3}{5}$ a²b^y与单项式2a^xb³是同类项，则x+y的值是（）

A、3 B、5 C、7 D、8

查看试题解析
6. 方程 $\frac{3 x - 7}{4} = \frac{x + 17}{5} - 1$ ，去分母得（）

A、 $5 (3 x - 7) = 4 (x + 17) - 1$ B、 $15 x - 35 = 4 x + 68$ C、 $5 (3 x - 7) = 4 x + 48$ D、 $5 (3 x - 7) = 4 (x + 17)$

查看试题解析
7. 下列变形正确的是（）

A、由 $\frac{x - 5}{3} - 1 = \frac{2 x + 1}{5}$ 去分母，得 $5 (x - 5) - 1 = 3 (2 x + 1)$ B、由 $3 (2 x - 1) - 2 (x + 5) = 4$ 去括号，得 $6 x - 3 - 2 x + 10 = 4$ C、由 $- 6 x - 1 = 2 x$ 移项，得 $- 6 x - 2 x = 1$ D、由 $2 x = 3$ 系数化为1， $x = \frac{2}{3}$

查看试题解析
8. 将一副三角板如图①的位置摆放，其中30°直角三角板的直角边与等腰直角三角板的斜边重合，30°直角三角板直角顶点与等腰直角三角板的锐角顶点重合（为点O）．现将30°的直角三角板绕点O顺时针旋转至如图②的位置，此时 $∠ 1$ 为25°，则 $∠ 2 =$ （）

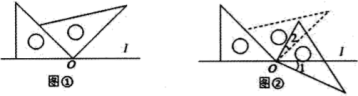A、15° B、20° C、25° D、30°

查看试题解析
9. 在光明区举办的“周年艺术季”期间，小颖一家去欣赏了一台音乐剧，路上预计用时25分钟，但由于堵车，所以实际车速比预计的每小时慢了10千米，且路上多用了5分钟．设预计车速为x千米/时，根据题意可列方程为（）

A、 $\frac{25}{60} x = \frac{30}{60} (x + 10)$ B、 $\frac{25}{60} (x + 10) = \frac{30}{60} x$ C、25x＝30x﹣10 D、 $\frac{25}{60} x = \frac{30}{60} (x - 10)$

查看试题解析
10. 如图，在同一平面内， $∠ A O B = ∠ C O D = 90 °$ ， $∠ A O F = ∠ D O F$ ，点 $E$ 为 $O F$ 反向延长线上一点（图中所有角均指小于 $180 °$ 的角）．下列结论：
① $∠ C O E = ∠ B O E$ ；
② $∠ A O D + ∠ B O C = 180 °$ ；
③ $∠ B O C - ∠ A O D = 90 °$ ；
④ $∠ C O E + ∠ B O F = 180 °$ ．其中正确结论的个数有（）

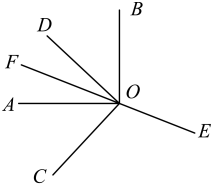A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 某企业对应聘人员进行专业考试，试题由50道不定项选择题组成，评分标准规定：每道题全选对得4分，不选得0分，选错或符合题意选项不全倒扣2分．已知某人有4道题未选，得了172分，则这个人全选对了道题．

查看试题解析
12. 在一条可以折叠的数轴上， $A$ ， $B$ 表示的数分别是 $- 9$ ， 4，如图，以点 $C$ 为折点，将此数轴向右对折，若点 $A$ 在点 $B$ 的右边，且 $A B = 1$ ，则点 $C$ 表示的数是．

查看试题解析
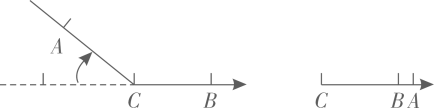13. 一项工程甲单独做9天完成，乙单独做12天完成．现甲、乙合作一段时间后乙休假，结果共用了6天完成这项工程．设乙休假x天，可列方程为．

查看试题解析
14. 在一张零件图中，如图，已知 $A D = 35 m m$ ， $B D = 32 m m$ ， $C D = 9 m m$ ，则 $A B =$ $m m$ ， $B C =$ $m m$ ．

查看试题解析
15. 如图所示是一个运算程序，若输出的结果是-2，则输入的值为．

查看试题解析

三、解答题

16. 计算：

(1)、 $8 + (- 10) + (- 2) - (- 5)$ ；

(2)、 $1 - \frac{4}{7} + \frac{1}{5} - \frac{3}{7} + \frac{9}{5}$ ；

(3)、 $(- 27) \div (- 3) \times \frac{1}{3} + {(- 1)}^{2023}$ ；

(4)、 $(\frac{1}{2} - \frac{5}{9} + \frac{7}{12}) \times (- 36)$ ．

查看试题解析
17.

(1)、化简： $- 3 a^{3} + 5 a - a^{3} + a$ ；

(2)、解方程： $\frac{1}{2} (3 x - 4) = \frac{1}{2} x - 2$ ．

查看试题解析
18. 某自行车厂计划平均每天生产自行车200辆，但是由于种种原因，实际每天生产量与计划量相比有出入．如表是某周的生产情况（超产记为正，减产记为负，单位：辆）：
星期一二三四五六日
增减 +6 -3 -8 +10 -10 +23 -4

(1)、该厂星期三生产自行车多少辆？

(2)、产量最多的一天比产量最少的一天多生产自行车多少辆？

(3)、该厂本周实际平均每天生产自行车多少辆？

查看试题解析
19. 如图是暖瓶与水杯的价格示意图．

(1)、一个暖瓶与一个水杯的价格分别是多少元？

(2)、甲、乙两家商场同时出售同样的暖瓶和水杯．为了迎接新年，两家商场都在搞促销活动．甲商场规定：这两种商品都打九折；乙商场规定：买一个暖瓶赠送一个水杯．若某单位想要买4个暖瓶和15个水杯，请问选择哪家商场购买更合算，并说明理由．

查看试题解析
20. 李明同学设计了某个产品的正方体包装盒如图所示，由于粗心少设计了其中一个顶盖，请你把它补上，使其成为一个两面均有盖的正方体盒子．

(1)、共有种弥补方法；

(2)、任意画出一种成功的设计图 $($ 在图中补充 $)$ ；

(3)、在你帮忙设计成功的图中，要把 $- 10$ ， $8$ ， $10$ ， $- 12$ ， $- 8$ ， $12$ 这些数字分别填入六个小正方形，使得折成的正方体相对面上的两个数相加得 $0 . ($ 直接在图中填上 $)$

查看试题解析
21. 如图1，点O为直线 $A B$ 上一点，过点O作射线 $O C$ ，使 $∠ B O C = 120 °$ ，将一直角三角板的直角顶点放在点O处，一边 $O M$ 在射线 $O B$ 上，另一边 $O N$ 在直线 $A B$ 的下方．

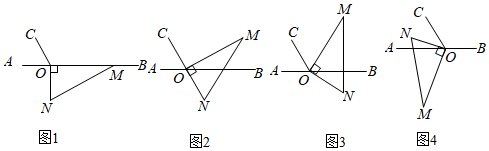(1)、将图1中的三角板绕点O逆时针旋转至图2，使点N在 $O C$ 的反向延长线上，请直接写出图中 $∠ M O B$ 的度数；

(2)、将图1中的三角板绕点O顺时针旋转至图3，使一边 $O M$ 在 $∠ B O C$ 的内部，且恰好平分 $∠ B O C$ ，求 $∠ C O N$ 的度数；

(3)、将图1中的三角尺绕点O顺时针旋转至图4，使 $O N$ 在 $∠ A O C$ 内部，请探究 $∠ A O M$ 与 $∠ N O C$ 之间的数量关系，并说明理由．

查看试题解析
22.
【背景知识】
数轴是我们学习数学的一个重要工具，利用数轴可以很好地将数与形结合．
如图，若数轴上 $A ， B$ 两点表示的数分别为 $a ， b$ ，则 $A ， B$ 两点之间的距离 $A B = | b - a |$ ，例如， $a = - 2 ， b = 1$ ，则 $A B = | 1 - (- 2) | = 1 - (- 2) = 3$ ．

(1)、【问题情境】
如图， $A ， B$ 两点在数轴上对应的数分别为 $- 8$ 和12，甲、乙分别从 $A ， B$ 处同时出发，甲的速度为1个单位长度/秒，乙的速度为3个单位长度/秒，设运动的时间为秒．
$A B =$ ．

(2)、【综合运用】
如果甲、乙相向运动（甲向右运动，乙向左运动），记相遇点为 $P$ ，则点 $P$ 表示的数为，此时 $t =$ ．

(3)、如果甲、乙都向左运动，
①当为何值时，乙恰好追上甲？
②当为何值时，甲、乙之间恰好相距5个单位长度？

查看试题解析

星期	一	二	三	四	五	六	日
增减	+6	-3	-8	+10	-10	+23	-4