广东省佛山市南海区2023-2024学年高二上学期11月期中考试数学试题
试卷更新日期:2023-12-09 类型:期中考试
一、选择题
-
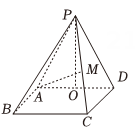
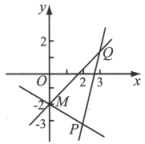
1. 如图,已知直线PM、QP、QM的斜率分别为、、 , 则、、的大小关系为( )
 A、 B、 C、 D、2. 在一个不透明的袋中有4个红球和个黑球,现从袋中有放回地随机摸出2个球,已知取出的球中至少有一个红球的概率为 , 则( )A、1 B、2 C、3 D、43. 如图,在空间四边形中, , , , 点满足 , 点为的中点,则( )
A、 B、 C、 D、2. 在一个不透明的袋中有4个红球和个黑球,现从袋中有放回地随机摸出2个球,已知取出的球中至少有一个红球的概率为 , 则( )A、1 B、2 C、3 D、43. 如图,在空间四边形中, , , , 点满足 , 点为的中点,则( )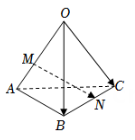 A、 B、 C、 D、4. 已知方程表示的曲线是椭圆,则实数的取值范围是( )A、 B、 C、 D、5. 若两异面直线 与 的方向向量分别是 , ,则直线 与 的夹角为( )A、30° B、60° C、120° D、150°6. 在圆:内,过点的最长弦和最短弦分别是和 , 则四边形的面积为( )A、24 B、12 C、10 D、87. 抛掷一枚质地均匀的骰子两次,设“第一次向上的点数是2”为事件 , “第二次向上的点数是奇数”为事件 , “两次向上的点数之和能被3整除”为事件 , 则下列说法正确的是( )A、事件与事件互为对立事件 B、 C、 D、事件与事件相互不独立8. 已知动点在正方体的对角线(不含端点)上.设 , 若为钝角,则实数的取值范围为( )
A、 B、 C、 D、4. 已知方程表示的曲线是椭圆,则实数的取值范围是( )A、 B、 C、 D、5. 若两异面直线 与 的方向向量分别是 , ,则直线 与 的夹角为( )A、30° B、60° C、120° D、150°6. 在圆:内,过点的最长弦和最短弦分别是和 , 则四边形的面积为( )A、24 B、12 C、10 D、87. 抛掷一枚质地均匀的骰子两次,设“第一次向上的点数是2”为事件 , “第二次向上的点数是奇数”为事件 , “两次向上的点数之和能被3整除”为事件 , 则下列说法正确的是( )A、事件与事件互为对立事件 B、 C、 D、事件与事件相互不独立8. 已知动点在正方体的对角线(不含端点)上.设 , 若为钝角,则实数的取值范围为( )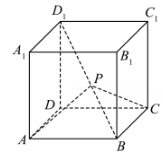 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 下列说法正确的是( )A、设 , 是两个随机事件,且 , , 则 B、若 , , , 则事件与事件相互独立 C、一个人连续射击2次,事件“两次均未击中”与事件“至多一次击中”互为对立事件 D、从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是10. 已知椭圆:的左、右焦点分别为 , , 点在上,且的最大值为3,最小值为1,则( )A、椭圆的离心率为 B、的周长为4 C、若 , 则的面积为 D、若 , 则11. 已知经过点的圆的圆心坐标为(为整数),且与直线:相切,直线:与圆相交于、两点,下列说法正确的是( )A、圆的标准方程为 B、若 , 则实数的值为 C、若 , 则直线的方程为或 D、弦的中点的轨迹方程为12. 如图,正方体中,为的中点,为棱上的动点,则下列结论正确的是( )
 A、存在点 , 使平面 B、存在点 , 使 C、四面体的体积为定值 D、二面角的余弦值取值范围是
A、存在点 , 使平面 B、存在点 , 使 C、四面体的体积为定值 D、二面角的余弦值取值范围是三、填空题
-
13. 已知直线经过椭圆的一个焦点和一个顶点,则此椭圆的离心率.14. 已知点 , 直线过原点 , 且平行于向量 , 则点到直线的距离是.15. 已知事件 , 相互独立,且 , , 则.16. 已知 , , 若直线上存在点 , 使得 , 则的取值范围是.
四、解答题
-
17. 如图,在中,边上的高所在的直线方程为 , 的平分线所在的直线方程为 , 若点的坐标为 , 求:
 (1)、点和点的坐标;(2)、求的面积.18. 学校为丰富同学们的课余活动,在体艺节活动中举办了艺术比赛,现甲乙两组进入到决赛阶段,决赛采用三局两胜制决出冠军,每一局比赛中甲组获胜的概率为 , 且甲组最终获得冠军的概率为(每局比赛没有平局)(1)、求;(2)、已知冠军奖品为28个礼品,在甲组第一局获胜后,比赛被迫取消,奖品分配方案是:如果比赛继续进行下去,按照甲乙两组各自获胜的概率分配礼品,请问按此方案,甲组、乙组分别可获得多少个礼品?19. 如图,已知正方体的棱长为4,点满足 , 点是的中点,点满足.
(1)、点和点的坐标;(2)、求的面积.18. 学校为丰富同学们的课余活动,在体艺节活动中举办了艺术比赛,现甲乙两组进入到决赛阶段,决赛采用三局两胜制决出冠军,每一局比赛中甲组获胜的概率为 , 且甲组最终获得冠军的概率为(每局比赛没有平局)(1)、求;(2)、已知冠军奖品为28个礼品,在甲组第一局获胜后,比赛被迫取消,奖品分配方案是:如果比赛继续进行下去,按照甲乙两组各自获胜的概率分配礼品,请问按此方案,甲组、乙组分别可获得多少个礼品?19. 如图,已知正方体的棱长为4,点满足 , 点是的中点,点满足.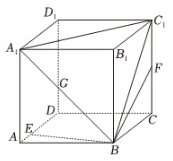 (1)、求证:、、、四点共面;(2)、求平面与平面夹角的余弦值
(1)、求证:、、、四点共面;(2)、求平面与平面夹角的余弦值