浙江省杭州竺可桢教育集团2023-2024学年九年级上学期期中阶段性检测数学试题
试卷更新日期:2023-12-08 类型:期中考试
一、选择题(本题有10个小题,每小题3分,共30分)
-
1. 一个不透明的盒子中装有2个红球和1个白球,它们除颜色外都相同,若从中任意摸出一个球,则下列叙述正确的是( )A、摸到红球是必然事件 B、摸到白球是不可能事件 C、摸到红球和摸到白球的可能性相等 D、摸到红球比摸到白球的可能性大2. 抛物线y=x2-2x的图象与x轴交点的横坐标分别是( )A、0,1 B、1,2 C、0,2 D、-1,-23. 如图在⊙O中,弦AB为8,圆心O到AB的距离为3,则⊙O的半径为( )
 A、3 B、4 C、5 D、84. 在指定的5个男生和3个女生中,随机抽调1人参加“湘湖”志愿服务队,恰好抽到男生的概率是( )A、1 B、 C、 D、5. 如图,已知四边形ABCD内接于⊙O,若∠ADC=110°,则∠AOC等于( )°.
A、3 B、4 C、5 D、84. 在指定的5个男生和3个女生中,随机抽调1人参加“湘湖”志愿服务队,恰好抽到男生的概率是( )A、1 B、 C、 D、5. 如图,已知四边形ABCD内接于⊙O,若∠ADC=110°,则∠AOC等于( )°. A、130 B、140 C、150 D、1606. 已知A(-5,y1),B(1,y2),C(2,y3)为二次函数y=x2+2x+m的图象上的三点,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y3<y1 C、y2<y1<y3 D、y3<y1<y27. 下列命题:①长度相等的弧是等弧;②过平面内三点可以作一个圆;③平分弦的直径垂直于弦;④90°的圆周角所对的弦是直径;⑤等弦对等弧 .其中正确的是( )A、1个 B、2个 C、3个 D、4个8. 在同一坐标系中,一次函数y=-mx+n2与二次函数y=x2+m的图象可能是( )A、
A、130 B、140 C、150 D、1606. 已知A(-5,y1),B(1,y2),C(2,y3)为二次函数y=x2+2x+m的图象上的三点,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y3<y1 C、y2<y1<y3 D、y3<y1<y27. 下列命题:①长度相等的弧是等弧;②过平面内三点可以作一个圆;③平分弦的直径垂直于弦;④90°的圆周角所对的弦是直径;⑤等弦对等弧 .其中正确的是( )A、1个 B、2个 C、3个 D、4个8. 在同一坐标系中,一次函数y=-mx+n2与二次函数y=x2+m的图象可能是( )A、 B、
B、 C、
C、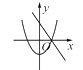 D、
D、 9. 如图,已知正六边形ABCDEF中,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的值最小时,BP与HG的夹角(锐角)度数为 ( )度.
9. 如图,已知正六边形ABCDEF中,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的值最小时,BP与HG的夹角(锐角)度数为 ( )度.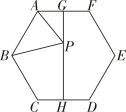 A、 B、60 C、 D、10. 二次函数、、是常数,且的自变量与函数值的部分对应值如下表:
A、 B、60 C、 D、10. 二次函数、、是常数,且的自变量与函数值的部分对应值如下表:x
…
-1
0
1
2
…
y … m 2 2 n … 且当时,对应的函数值有以下结论:;;关于的方程的负实数根在和之间;和在该二次函数的图象上,则当实数时, .
其中正确的结论是( )A、 B、 C、 D、二、填空题(本题有 6 个小题,每小题 4 分,共 24 分)
-
11. 已知扇形的圆心角为120°,半径为2,则这个扇形的面积=.12. 一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率 .
 13. 将二次函数y=(x-2)2-3的图象向右平移2个单位,再向上平移3个单位后得到新函数表达式是.14. 在⊙O中,若弦BC垂直平分半径OA,则弦BC所对的圆周角等于15. 已知二次函数(m为常数)的图象与x轴有交点,且当x<-3时,y随x的增大而增大,则m的取值范围是16. 如图,在等腰Rt△ABC中,AC=BC=3,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是 .
13. 将二次函数y=(x-2)2-3的图象向右平移2个单位,再向上平移3个单位后得到新函数表达式是.14. 在⊙O中,若弦BC垂直平分半径OA,则弦BC所对的圆周角等于15. 已知二次函数(m为常数)的图象与x轴有交点,且当x<-3时,y随x的增大而增大,则m的取值范围是16. 如图,在等腰Rt△ABC中,AC=BC=3,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是 .
三、解答题(共66分)
-
17. 小红的爸爸积极参加社区亚运志愿服务工作,根据社区的安排,志愿者被随机分到A组(巡逻服务),B组(询问服务),C组(茶水服务).(1)、小红的爸爸被分到B组的概率是;(2)、某中学王老师也参加了该社区的志愿者队伍,他和小红爸爸被分到同一组的概率是多少?(请用画树状图或列表的方法写出分析过程)18. 求下列函数解析式(1)、已知二次函数顶点坐标是(-2,1),形状与此二次函数相同(2)、已知二次函数过点(3,0),(1,8)(-1,0)19. 如图所示,在△ABC中,BE=CE,∠C=70°,以AB为直径的半圆分别交AC、BC于点D,E,O为圆心,求∠DOE的度数.
 20. 如图,已知一次函数-x+m与二次函数-3图象交于A(-1,0)、B(2,-3)两点.
20. 如图,已知一次函数-x+m与二次函数-3图象交于A(-1,0)、B(2,-3)两点. (1)、求m的值和二次函数图象的对称轴(2)、当时,直接写出自变量x的取值范围.21. 如图,AB是⊙O的直径,点C为⊙O上一点,D为弧BC的中点,过D作DF⊥AB于点E,交⊙O于点F,交弦BC于点G,连接CD,BF.
(1)、求m的值和二次函数图象的对称轴(2)、当时,直接写出自变量x的取值范围.21. 如图,AB是⊙O的直径,点C为⊙O上一点,D为弧BC的中点,过D作DF⊥AB于点E,交⊙O于点F,交弦BC于点G,连接CD,BF. (1)、求证:BC=DF.(2)、若BC=8,BE=2,求⊙O的半径.22. 某商场以每件42元的价格购进一批商品,经试销发现,若每件商品售价60 元,则每天可卖出50件,若售价每降低2元,则每天可多卖10件,根据相关规定,每件售价60元已达到毛利润上限,不能再涨价,但也不能以低于进价销售,在销售过程中,商场每天还需支付其它费用共200元.(1)、写出每天销售量 y(件)与销售单价m(元)之间的函数关系式,并指出自变量m范围.(2)、商场应把售价定为多少元才能使每天获得的利润最大?最大利润是多少元?
(1)、求证:BC=DF.(2)、若BC=8,BE=2,求⊙O的半径.22. 某商场以每件42元的价格购进一批商品,经试销发现,若每件商品售价60 元,则每天可卖出50件,若售价每降低2元,则每天可多卖10件,根据相关规定,每件售价60元已达到毛利润上限,不能再涨价,但也不能以低于进价销售,在销售过程中,商场每天还需支付其它费用共200元.(1)、写出每天销售量 y(件)与销售单价m(元)之间的函数关系式,并指出自变量m范围.(2)、商场应把售价定为多少元才能使每天获得的利润最大?最大利润是多少元?
