浙江省杭州竺可桢教育集团2023-2024学年八年级上学期期中阶段性检测数学试题

试卷更新日期：2023-12-08 类型：期中考试

进入出卷网下载

一、仔细选一选（每小题3分）

1. 下列四个图形中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列长度（单位：cm）的三条线段能组成三角形的是（）

A、5，5，13 B、1，2，3 C、5，7，12 D、11，12，13

查看试题解析
3. 如图，已知点A、D、C、F在同一条直线上，AB＝DE，BC＝EF，要使△ABC≌△DEF，还需要添加一个条件是（）

A、∠BCA＝∠F B、∠B＝∠E C、BC∥EF D、∠A＝∠EDF

查看试题解析
4. 若x＞y，则下列式子中错误的是（）

A、x﹣3＞y﹣3 B、 $\frac{x}{3}$ > $\frac{y}{3}$ C、x+3＞y+3 D、﹣3x＞﹣3y

查看试题解析
5. 用直尺和圆规作一个角等于已知角，如图，能得出∠A′O′B′＝∠AOB的依据是（　　）

A、（SAS） B、（SSS） C、（ASA） D、（AAS）

查看试题解析
6. 下列条件中，不能判断一个三角形是直角三角形的是（）

A、三个角的比为1：2：3 B、三条边满足关系a²=b²﹣c² C、三条边的比为1：2：3 D、三个角满足关系∠B+∠C=∠A

查看试题解析
7. 如图，AD是△ABC的角平分线，DE⊥AB于点E，S_△_ABC＝9，DE＝2，AB＝5，则边AC的长是（　　）

A、3 B、4 C、5 D、6

查看试题解析
8. 物美超市（滨江浦沿店）某商品的标价比成本价高m%，根据市场需要，该商品需降价n%出售，为了不亏本，n应满足（　　）

A、n≤m B、 $n ⩽ \frac{100 m}{100 + m}$ C、 $n ⩽ \frac{m}{100 + m}$ D、 $n ⩽ \frac{100 m}{100 - m}$

查看试题解析
9. 如图，四边形ABCD是正方形，直线a，b，c分别通过A、D、C三点，且a∥b∥c．若a与b之间的距离是5，b与c之间的距离是7，则正方形ABCD的面积是（　　）

A、148 B、144 C、74 D、70

查看试题解析
10. 如图，正方形网格中的每个小正方形边长都是1．已知A、B是两格点，若△ABC为等腰三角形，且S_△ABC＝1.5，则满足条件的格点C有（）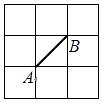

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、认真填一填（每小题4分）

11. 命题“如果a+b＞0，那么a＞0，b＞0”的逆命题是.

查看试题解析
12. 不等式（a﹣b）x＜a﹣b的解集是x＞1，则a、b的大小关系是：ab．

查看试题解析
13. 等腰三角形的两条边长为2，4，则等腰三角形的周长为

查看试题解析
14. 等腰三角形有一个角是36°，则它的顶角度数是．

查看试题解析
15. 已知关于x的不等式组 ${\begin{array}{l} x - a ⩾ 0 \\ 3 - 2 x > - 1 \end{array}$ 的整数解有3个，则a的取值范围是．

查看试题解析
16. 如图，∠BOC＝ɑ°，点A在OB上，且OA＝1，按下列要求画图：
以A为圆心，1为半径向右画弧交OC于点A₁ ，得第1条线段AA₁；
再以A₁为圆心，1为半径向右画弧交OB于点A₂ ，得第2条线段A₁A₂；
再以A₂为圆心，1为半径向右画弧交OC于点A₃ ，得第3条线段A₂A₃；…
这样画下去，直到得第n条线段，之后就不能再画出符合要求的线段了，
则当ɑ=20°时n＝；求出的ɑ取值范围（用含有n的代数式表示）．

查看试题解析

三、全面答一答解答应写出文字说明，证明过程或推演步骤．

17. 解不等式 5x＞3（x-2）+2

查看试题解析
18. 如图，在Rt△ABC中，∠ACB＝90°．

(1)、尺规作图在边BC上求作一点P，使PA＝PB，并连接AP；（不写作法，保留作图痕迹）

(2)、在（1）的条件下，当AC＝3，AB＝5时，求△ACP的周长；

查看试题解析
19. 如图，四边形ABCD的对角线AC与BD相交于O点，∠1＝∠2，∠3＝∠4．
求证：△ABC≌△ADC；AC垂直平分BD．

查看试题解析
20. 如图，△ABC是等边三角形，BD⊥AC，AE⊥BC，垂足分别为D、E，AE、BD相交于点O，连接DE．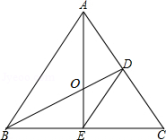

(1)、判断△CDE的形状，并说明理由．

(2)、若AO＝12，求OE的长．

查看试题解析
21. 金盛嘉悦广场销售每台进价分别为200元，170元的A、B两种型号的电风扇，表中是近两周的销售情况：
销售时段销售数量销售收入
A种型号 B种型号
第一周 3台 5台 1800
第二周 4台 10台 3100
（进价、售价均保持不变，利润＝销售收入-进货成本）

(1)、求A、B两种型号的电风扇的销售单价；

(2)、若金盛嘉悦广场准备用不多于5400元的金额再采购这两种型号的电风扇共30台，求A种型号的电风扇最多能采购多少台？

(3)、在（2）的条件下，金盛嘉悦广场销售完这30台电风扇能否实现利润为1400元的目标？若能，请给出相应的采购方案；若不能，请说明理由．

查看试题解析
22. 在Rt△ABC中，∠ACB＝90°，M是边AB的中点，CH⊥AB于点H，CD平分∠ACB．

(1)、求证：CD平分∠MCH；

(2)、过点M作AB的垂线交CD的延长线于点E，
①求证：CM＝EM；
②△AEM是什么三角形？证明你的猜想．

查看试题解析
23. 我们用[a]表示不大于a的最大整数，例如：[2.5]＝2，[3]＝3，[-2.5]＝-3；用＜a＞表示大于a的最小整数，例如：＜2.5＞＝3，＜3＞＝4，＜-2.5＞＝-2．根据上述规定，解决下列问题：

(1)、[-4.5]＝，＜3.01＞＝；

(2)、若x为整数，且[x]+＜x＞＝2023，求x的值；

(3)、若x、y满足方程组 ${\begin{array}{l} 3 [x] + 2 < y > = 3 \\ 3 [x] - < y > = - 6 \end{array}$ ，求x、y的取值范围．

查看试题解析
24. 如图，△ABC中，∠C＝90°，AC＝8cm，BC＝6cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒2cm，设运动的时间为t秒．

(1)、当t=1时，求△PBC的面积．

(2)、当t为何值时，CP把△ABC的面积分成相等的两部分，并求出此时CP的长；

(3)、当t为何值时，△BCP为等腰三角形？

查看试题解析

销售时段	销售数量		销售收入
销售时段	A种型号	B种型号	销售收入
第一周	3台	5台	1800
第二周	4台	10台	3100