浙江省宁波市江北区五校2023-2024学年九年级上学期期中数学试题
试卷更新日期:2023-12-08 类型:期中考试
一、选择题(本大题有10小题,每小题3分,共30分)
-
1. 抛物线的对称轴是( )A、直线 B、直线 C、直线 D、直线2. 下列事件是必然事件的是( )A、任意一个三角形的内角和等于 B、投掷一个均匀的硬币100次,正面朝上的次数是50次 C、射击运动员射击一次,命中10环 D、宁波今年冬天会下雪3. 等腰中, , 以点A为圆心,的长为半径画 , 则点C与的位置关系是( )A、点C在内 B、点C在上 C、点C在外 D、以上均不可能4. 如图,在中,点D、E分别是边、上的中点,则的值为( )
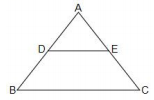 A、2 B、 C、4 D、5. 某射击运动员在同一条件下的射击成绩记录如下:
A、2 B、 C、4 D、5. 某射击运动员在同一条件下的射击成绩记录如下:射击次数
20
80
100
200
400
1000
“射中8环以上”的次数
18
68
82
168
327
823
“射中8环以上”的频率(结果保留两位小数)
0.90
0.85
0.82
0.84
0.82
0.82
根据频率的稳定性,估计这名运动员射击一次时“射中8环以上”的概率约是( )
A、0.90 B、0.82 C、0.85 D、0.846. 如图,是的直径,点A、C是圆上不与点B、D重合的两个点,若 , 则的度数为( )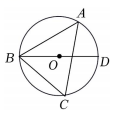 A、 B、 C、 D、7. 将抛物线向右平移1个单位,再向上平移2个单位后,得到的新的抛物线的解析式为( )A、 B、 C、 D、8. 如图,为测量学校旗杆的高度,小明用长为3.2m的竹竿作测量工具,移动竹竿,使竹竿顶端与旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为( )
A、 B、 C、 D、7. 将抛物线向右平移1个单位,再向上平移2个单位后,得到的新的抛物线的解析式为( )A、 B、 C、 D、8. 如图,为测量学校旗杆的高度,小明用长为3.2m的竹竿作测量工具,移动竹竿,使竹竿顶端与旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为( )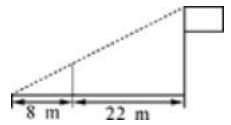 A、8.8m B、10m C、12m D、14m9. 若、、为二次函数的图象上的三点,则、、的大小关系是( )A、 B、 C、 D、10. 如图,直线与y轴交于点A,与直线交于点B,以为边向右作菱形 , 点C恰与原点O重合,抛物线的顶点在直线上移动.若抛物线与菱形的边、都有公共点,则h的取值范围是( )
A、8.8m B、10m C、12m D、14m9. 若、、为二次函数的图象上的三点,则、、的大小关系是( )A、 B、 C、 D、10. 如图,直线与y轴交于点A,与直线交于点B,以为边向右作菱形 , 点C恰与原点O重合,抛物线的顶点在直线上移动.若抛物线与菱形的边、都有公共点,则h的取值范围是( )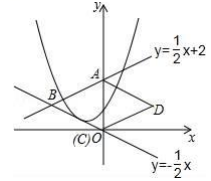 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题有6小题,每小题4分,共24分)
-
11. 若 , 则 .
12. 二次函数的图象开口方向向上,则a的取值范围 .13. 不透明袋子中装有1个红球和2个黄球,这些球除颜色外无其他差别.从袋子中随机摸出1个球,摸出红球的概率是14. 如图,内接于 , 是的直径,连结 , 若 , , 则的半径为 .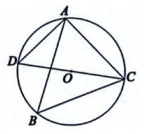 15. 已知抛物线的部分图象如图所示,当时,则x的取值范围是 .
15. 已知抛物线的部分图象如图所示,当时,则x的取值范围是 .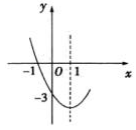 16. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.将小正方形对角线双向延长,分别交边 , 和边的延长线于点G,H.若大正方形与小正方形的面积之比为5, , 则大正方形的边长为 .
16. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.将小正方形对角线双向延长,分别交边 , 和边的延长线于点G,H.若大正方形与小正方形的面积之比为5, , 则大正方形的边长为 .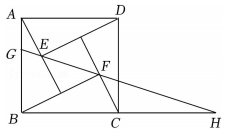
三、解答题(本大题有8小题,第17、18题每题6分,第19、20、21、22题每题8分,第23题10分,第24题12分,共66分)
-
17. 如图,正三角形网格中,已知两个小正三角形被涂黑.
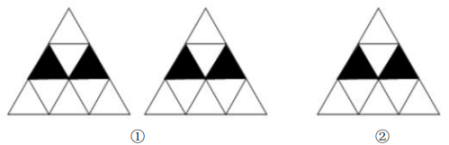 (1)、再将图①中其余小三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形(画出两种不同的涂法);(2)、再将图②中其余小三角形涂黑两个,使整个被涂黑的图案构成一个中心对称图形.18. 一只不透明的袋子中装有3个球,球上分别标有数字0,1,2,这些球除了数字外其余都相同,甲、乙两人玩摸球游戏,规则如下:先由甲随机摸出一个球(不放回),再由乙随机摸出一个球,两人摸出的球所标的数字之和为偶数时则甲胜,和为奇数时则乙胜.(1)、用画树状图或列表的方法列出所有可能的结果;(2)、这样的游戏规则是否公平?请说明理由.19. 如图,在平面直角坐标系中,已知的三个顶点的坐标分别为 , , .
(1)、再将图①中其余小三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形(画出两种不同的涂法);(2)、再将图②中其余小三角形涂黑两个,使整个被涂黑的图案构成一个中心对称图形.18. 一只不透明的袋子中装有3个球,球上分别标有数字0,1,2,这些球除了数字外其余都相同,甲、乙两人玩摸球游戏,规则如下:先由甲随机摸出一个球(不放回),再由乙随机摸出一个球,两人摸出的球所标的数字之和为偶数时则甲胜,和为奇数时则乙胜.(1)、用画树状图或列表的方法列出所有可能的结果;(2)、这样的游戏规则是否公平?请说明理由.19. 如图,在平面直角坐标系中,已知的三个顶点的坐标分别为 , , .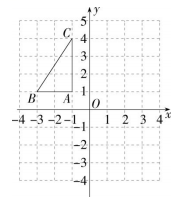 (1)、的外接圆的半径为;(2)、将绕点B顺时针旋转后得到 , 请在图中画出;(3)、在(2)的条件下,求出点C经过的路径长.20. 如图,为的直径,是弦,且于点E.连接、、 .
(1)、的外接圆的半径为;(2)、将绕点B顺时针旋转后得到 , 请在图中画出;(3)、在(2)的条件下,求出点C经过的路径长.20. 如图,为的直径,是弦,且于点E.连接、、 .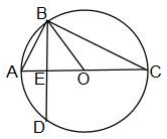 (1)、求证:;(2)、若 , , 求弦的长.21. 如图,已知二次函数的图象经过点、点 .
(1)、求证:;(2)、若 , , 求弦的长.21. 如图,已知二次函数的图象经过点、点 .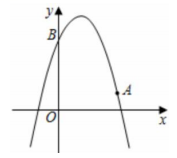 (1)、求该二次函数的表达式及顶点坐标.(2)、点在该二次函数图象上.
(1)、求该二次函数的表达式及顶点坐标.(2)、点在该二次函数图象上.①当时,求n的值;
②当时,n的最大值为5,最小值为1,请根据图象直接写出m的取值范围.
22. 如图,在等腰直角中, , , 点D、E分别在边、上(不与点A、B、C重合),连接、 , 有 .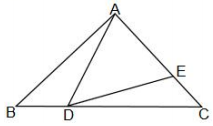 (1)、证明: .(2)、若 , 当是等腰三角形时,求的长.23. 随着近几年宁波城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木.根据市场调查与预测,种植树木的利润与投资量x成正比例关系,如图①所示;种植花卉的利润与投资量x成二次函数关系,如图②所示(利润与投资量的单位:万元)
(1)、证明: .(2)、若 , 当是等腰三角形时,求的长.23. 随着近几年宁波城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木.根据市场调查与预测,种植树木的利润与投资量x成正比例关系,如图①所示;种植花卉的利润与投资量x成二次函数关系,如图②所示(利润与投资量的单位:万元)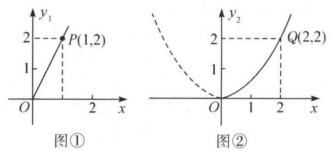 (1)、分别求出利润与关于投资量x的函数关系式.(2)、如果这个专业户以8万元资金投入种植花卉和树木,则他至少可以获得多少利润,他能获取的最大利润是多少.24. 如图1,E点为x轴正半轴上一点,交x轴于A、B两点,交y轴于C、D两点,P点为劣弧上一个动点,且、 .
(1)、分别求出利润与关于投资量x的函数关系式.(2)、如果这个专业户以8万元资金投入种植花卉和树木,则他至少可以获得多少利润,他能获取的最大利润是多少.24. 如图1,E点为x轴正半轴上一点,交x轴于A、B两点,交y轴于C、D两点,P点为劣弧上一个动点,且、 . (1)、的度数为;(2)、如图2,连结 , 取中点G,连结 , 则的最大值为;(3)、如图3,连接、、、 . 若平分交于Q点,求的长;(4)、如图4,连接、 , 当P点运动时(不与B、C两点重合),求证:为定值,并求出这个定值.
(1)、的度数为;(2)、如图2,连结 , 取中点G,连结 , 则的最大值为;(3)、如图3,连接、、、 . 若平分交于Q点,求的长;(4)、如图4,连接、 , 当P点运动时(不与B、C两点重合),求证:为定值,并求出这个定值.