浙江省湖州市南浔区九校2023-2024学年七年级上学期期中联考数学试题

试卷更新日期：2023-12-08 类型：期中考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. $- \frac{1}{2}$ 的相反数是（）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、 $- 2$ D、2

查看试题解析
2. 南浔冬季某天的最高气温 $9 ° C$ ，最低气温 $- 1 ° C$ ，这一天最高气温比最低气温高（）

A、 $10 ° C$ B、 $- 10 ° C$ C、 $8 ° C$ D、 $- 8 ° C$

查看试题解析
3. 下列运算正确的是（）

A、 $a^{3} - a^{2} = a$ B、 $- a + 5 a = 4 a$ C、 $a + a^{2} = a^{3}$ D、 $a b^{2} + a^{2} b = a b^{2}$

查看试题解析
4. 餐桌边的一蔬一饭，舌尖上的一饮一酌，实属来之不易，舌尖上的浪费让人触目惊心．据统计，中国每年浪费的食物总量折合粮食约530亿千克，这个数据用科学记数法表示为（）

A、 $530 \times 1 0^{8}$ 千克 B、 $53 \times 1 0^{9}$ 千克 C、 $5.3 \times 1 0^{10}$ 千克 D、 $0.53 \times 1 0^{11}$ 千克

查看试题解析
5. 如果 $2 x^{n + 2} y^{3}$ 与 $- 3 x^{3} y^{2 m - 1}$ 是同类项，那么m，n的值是（）

A、 $m = 2$ ， $n = 1$ B、 $m = 0$ ， $n = 1$ C、 $m = 2$ ， $n = 2$ D、 $m = 1$ ， $n = 2$

查看试题解析
6. 若 $| a - 2 |$ 与 $| m + n + 3 |$ 互为相反数，则 $a + m + n =$ （）

A、5 B、 $- 5$ C、1 D、 $- 1$

查看试题解析
7. 定义新运算“*”，规定 $a * b = a \times b - (b - 1) \times b$ ，则 $2 * (- 3)$ 的值为（）

A、6 B、 $- 18$ C、 $- 6$ D、18

查看试题解析
8. 若2023的两个平方根是 $m$ 和 $n$ ，则 $m + 2 m n + n$ 的值是（）

A、0 B、2023 C、 $- 4046$ D、4046

查看试题解析
9. 正方形 $A B C D$ 在数轴上的位置如图所示，点A、D对应的数分别为0和 $- 1$ ，若正方形 $A B C D$ 绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1；…，则连续翻转2023次后，数轴上数2023所对应的点是（）

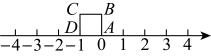A、点A B、点B C、点C D、点D

查看试题解析
10. 蛟蛟和川川一起玩拼图游戏，蛟蛟将六块拼图拼成如图所示的长方形 $A B C D$ ，其中 $① ② ③ ④$ 为正方形，川川发现如果知道 $⑤ ⑥$ 两块拼图的周长差，就可以知道其中一块正方形的边长了，那么这个正方形（）

A、① B、② C、③ D、④

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 计算： $\sqrt{16}$ = ．

查看试题解析
12. 比较大小：-2 3 （用“ $>$ 或 $=$ 或 $<$ ”填空）．

查看试题解析
13. 已知 $5 m + 3 n = 2$ ，那么 $10 m + 6 n - 5 =$ ．

查看试题解析
14. 已知 $2 a - 1$ 的平方根是 $\pm 3$ ， $c$ 是 $\sqrt{17}$ 的整数部分，则 $a + c$ 的值为．

查看试题解析
15. 有一个数值转换器，原理如下：当输入的 $x$ 为 $64$ 时，输出的 $y$ 的值．

查看试题解析
16. 如图，A点的初始位置位于数轴上表示1的点，现对A点做如下移动：第1次向左移动3个单位长度至B点，第2次从B点向右移动6个单位长度至C点，第3次从C点向左移动9个单位长度至D点，第4次从D点向右移动12个单位长度至E点，…，依此类推，则点E在数轴上所表示的数为，这样第次移动到的点到原点的距离为2020．

查看试题解析

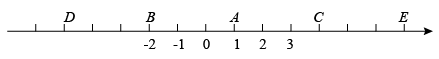
三、解答题（本题有8小题，共66分）

17. 把下列各数对应的序号填在相应的括号里.
①0 ， ② $\sqrt{5}$ ， ③ $- 3.5$ ，④ $π$ ， ⑤ $- \frac{12}{7}$ ， ⑥ $\sqrt[3]{- 27}$ ， ⑦ $| - 8 |$ ， ⑧ $1.202002 \dots$ （每两个“2”之间依次多一个“0” ）.
正整数：（）
负分数：（）
无理数：（）

查看试题解析
18. 计算：

(1)、 $8 - (- 4) - (+ 3) - 5$

(2)、 $- \frac{9}{10} \div \frac{2}{5} \times (- 2 \frac{1}{2})$

(3)、 $(\frac{1}{2} - \frac{5}{9} + \frac{5}{6} - \frac{7}{12}) \times (- 36) + {(- 3)}^{2}$

(4)、 $- 1^{2} + 16 \div (- 2)^{3} \times (- 3 - 1)$

查看试题解析
19.

(1)、计算： $2 a^{2} + 9 b - 5 a^{2} - 4 b$

(2)、先化简，再求值： $3 m n^{2} + m^{2} n - 2 (2 m n^{2} - m^{2} n)$ ，其中 $m = 1 ， n = - 2$ ．

查看试题解析
20. 出租车司机老姚某天上午8：00～9：15的营运全是在东西走向的解放路上进行，如果规定向东为正，向西为负．他这天上午行车里程（单位：km）如下：+5，-3，+6，-7，+6，-2，-5，-4，+6，-8．

(1)、将第几名乘客送到目的地时，老姚刚好回到上午出发点？

(2)、将最后一名乘客送到目的地时，老姚距上午出发点多远？在出发点的东面还是西面？

查看试题解析
21. 观察下列两个等式： $2 - \frac{1}{3} = 2 \times \frac{1}{3} + 1$ ， $5 - \frac{2}{3} = 5 \times \frac{2}{3} + 1$ 给出定义如下：我们称使等式 $a - b = a b + 1$ 成立的一对有理数“a，b”为“共生有理数对”，记为 $(a ， b)$ ，如：数对 $(2 ， \frac{1}{3})$ ， $(5 ， \frac{2}{3})$ 都是“共生有理数对”．

(1)、通过计算判断数对 $(1 ， 2)$ 是不是“共生有理数对”；

(2)、若 $(m ， n)$ 是“共生有理数对”，则 $(- n ， - m)$ “共生有理数对”（填“是”或“不是”）；

(3)、如果 $(m ， n)$ 是“共生有理数对”，且 $m - n = 4$ ，求 ${(- 5)}^{m n}$ 的值．

查看试题解析
22. 某超市在双十一期间对顾客实行优惠，规定如下：
一次性购物优惠办法
少于200元不予优惠
低于500元但不低于200元八折优惠
500元或超过500元其中500元部分给予八折优惠，超过500元部分给予七折优惠

(1)、若王老师一次性购物600元，他实际付款元．若王老师实际付款160元，那么王老师一次性购物可能是元；

(2)、若顾客在该超市一次性购物x元，当x小于500元但不小于200时，他实际付款元，当x大于或等于500元时，他实际付款元（用含x的代数式表示并化简）；

(3)、如果王老师有两天去超市购物原价合计900元，第一天购物的原价为a元（ $200 < a < 300$ ），用含a的代数式表示这两天购物王老师实际一共付款多少元？当 $a = 250$ 元时，王老师两天一共优惠了多少元？

查看试题解析
23. 如图，有这样一个探究：把两个边长为1的小正方形分别沿对角线剪开，将所得的4个直角三角形拼在一起，可以得到一个面积为2的大正方形，试根据这个研究方法回答下列问题：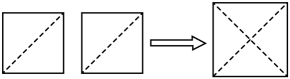

(1)、所得到的面积为2的大正方形的边长就是原边长为1的小正方形的对角线长，因此可得小正方形的对角线长为；

(2)、由此我们得到一种在数轴上找到无理数的方法：如下图，以单位长度为边长画一个正方形，以数字1所在的点为圆心，正方形的对角线为半径画弧，与数轴交于 $A$ 、 $B$ 两点，那么 $A$ 点表示的数为；

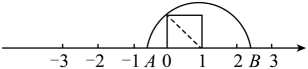(3)、通过动手操作，漠子同学把长为5，宽为1的长方形进行裁剪，拼成如图所示的正方形．请借鉴（2）中的方法在数轴上找到表示 $\sqrt{5} - 1$ 的点 $P$ ．（保留作图痕迹并标出必要线段长）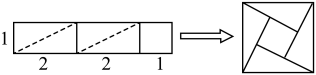

查看试题解析
24. 如图，已知数轴上两点A、B对应的数分别为a、b，且|a+4|+（b-12）²＝0．动点P从点B出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t秒（t＞0）．

(1)、写出数轴上点A表示的数为，点B表示的数为，点P表示的数为（用含t的式子表示）；

(2)、动点Q从点A出发，以每秒3个单位长度的速度向左匀速运动，动点M从点B出发，以每秒1个单位长度的速度向右匀速运动，且点P、Q、M同时出发．
①当t为何值时，点P、Q两点到点A的距离相等？
②式子mBQ-2MP的值不随时间t的变化而变化，求m的值．

查看试题解析

一次性购物	优惠办法
少于200元	不予优惠
低于500元但不低于200元	八折优惠
500元或超过500元	其中500元部分给予八折优惠，超过500元部分给予七折优惠