广东省深圳市龙华区2023-2024学年九年级上学期期中数学试题
试卷更新日期:2023-12-08 类型:期中考试
一、选择题:本大题共10小题,每小题3分,共30分。每小题只有一个选项符合题目要求。
-
1. 将一元二次方程化成一般形式之后,则一次项系数和常数项分别为( )A、 , B、5, C、5,7 D、 , 52. 若四条线段a,b,c,d是成比例线段,其中b=3cm,c=6cm,d=9cm,则线段a的长度为( )A、8cm B、2cm C、4cm D、1cm3. 如图,若直线l1∥l2∥l3 , 且DE:EF=3:4,AB=6,则BC=( )
 A、5 B、8 C、9 D、104. 若 , 是方程的两个根,则的值是( )A、 B、15 C、 D、55. 用配方法解一元二次方程 , 配方后可变形为( )A、 B、 C、 D、6. 如图,延长的边到 , 使 , 连接 , , .再添加一个条件,不能使四边形成为矩形的是( )
A、5 B、8 C、9 D、104. 若 , 是方程的两个根,则的值是( )A、 B、15 C、 D、55. 用配方法解一元二次方程 , 配方后可变形为( )A、 B、 C、 D、6. 如图,延长的边到 , 使 , 连接 , , .再添加一个条件,不能使四边形成为矩形的是( ) A、 B、 C、 D、7. 一次聚会,每两个参加聚会的人互送一件不同的小礼物,有人统计一共送了56件小礼物,如果参加这次聚会的人数为 , 根据题意可列方程为( )A、 B、 C、 D、8. 如图,将边长为的正方形沿其对角线剪开,再把沿方向平移,得到 , 若两个三角形重叠部分的面积是 , 则它移动的距离等于( )
A、 B、 C、 D、7. 一次聚会,每两个参加聚会的人互送一件不同的小礼物,有人统计一共送了56件小礼物,如果参加这次聚会的人数为 , 根据题意可列方程为( )A、 B、 C、 D、8. 如图,将边长为的正方形沿其对角线剪开,再把沿方向平移,得到 , 若两个三角形重叠部分的面积是 , 则它移动的距离等于( ) A、 B、 C、 D、9. 如图,用七支长度相同的铅笔,排成一个菱形和一个等边 , 使得点 , 分别在和上,那么的度数为( )
A、 B、 C、 D、9. 如图,用七支长度相同的铅笔,排成一个菱形和一个等边 , 使得点 , 分别在和上,那么的度数为( ) A、 B、 C、 D、10. 如图,正方形ABCD中,P是对角线BD上一点,过P作PE⊥BC,PF⊥DC,垂足分别为E、F,连接EF,若EF= , , 点D到AP的距离( )
A、 B、 C、 D、10. 如图,正方形ABCD中,P是对角线BD上一点,过P作PE⊥BC,PF⊥DC,垂足分别为E、F,连接EF,若EF= , , 点D到AP的距离( )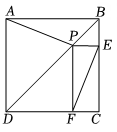 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共5小题,每小题3分,共15分)
-
11. 已知关于的方程有实数根,则的取值范围是.12. 一个盒子中装有20颗蓝色幸运星,若干题红色幸运星和15颗黄色幸运星,小明通过多次摸取幸运星试验后发现,摸取到红色幸运星的频率稳定在0.5左右,则摸到红色幸运星颗数约为颗.13. 如图,一张的纸片,在边上,将点折至点时,为折痕,其中点在边上,若的面积为100,的面积为60,则.
 14. 如图,若菱形的面积为 , , 将菱形折叠,使点恰好落在菱形对角线的交点处,折痕为 , 则cm.
14. 如图,若菱形的面积为 , , 将菱形折叠,使点恰好落在菱形对角线的交点处,折痕为 , 则cm.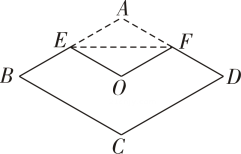 15. 在△ABC中,AD是∠BAC的角平分线,BE⊥AD交线段AD于点E,AB= , AC=5,BC=4,则△BEC的面积为。
15. 在△ABC中,AD是∠BAC的角平分线,BE⊥AD交线段AD于点E,AB= , AC=5,BC=4,则△BEC的面积为。
三、解答题(共7小题)
-
16. 解方程:(1)、;(2)、;(3)、.17. 不透明的盒中有4个完全相同的球,球上分别标有数字“1,2,3,4”.(1)、若从盒中随机取出1个球,取出的球上的数字是奇数的概率是;(2)、若从盒中取出一个球,记录球上的数字后不放回.再从剩下的球中取出一个球,并再次记录球上的数字,求两次数字的和为偶数的概率是多少?通过画树状图或列表法解决.18. 大新同学在学习北师大版九上第一章《特殊平行四边形》,通过习题1.4的第4题,知道了“如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。”大新设计了一个新的游戏机:如图1,用点表示灯泡,外圈8个灯泡平均分布在大圆内,内圈8个灯泡也平均分布在同一个圆心的小圆上,亮着的4个灯泡形成平行四边形。规定每一次4个灯泡亮,若形成某个特殊平行四边形,可换取对应的五角星★数;示例:图1,可获得.
 (1)、如果其中亮起的3个灯号为、、三点,则第4个亮着的灯号为哪一.点时,获得的★数?请在图2上画出对应的图形.(2)、如果获得 , 其中亮起的2个灯号为、两点,则另外2个亮着的灯号可能为哪两个?并请在图3上画出所有的可能的情况.19. 随着“一盔一带”安全守护行动在全国各地积极开展,道路上不戴头盔骑行的现象得到了极大的改善,七七超市的某品牌头盔的销量逐月攀升,已知4月份销售150个,6月份销售216个,且从4月份到6月份销售量的月增长率相同.(1)、求该品牌头盔销售量的月平均增长率;(2)、若此头盔的进价为30元/个,经测算当售价为40元/个时,月销售量为300个;售价每上涨1元,则月销售量减少10个,为使月销售利润达到3960元,并尽可能让顾客得到实惠,则该品牌头盔的售价应定为多少元/个?20. 如图1,在中,的角平分线交边于点 , 甲、乙两人想作菱形 , 使得、两点分别在边和边上,他们的作法如下:甲:作的中垂线分别交、于点、 , 连接、 , 则四边形即为所求;乙:分别作交边于点 , 交于点 , 则四边形即为所求.
(1)、如果其中亮起的3个灯号为、、三点,则第4个亮着的灯号为哪一.点时,获得的★数?请在图2上画出对应的图形.(2)、如果获得 , 其中亮起的2个灯号为、两点,则另外2个亮着的灯号可能为哪两个?并请在图3上画出所有的可能的情况.19. 随着“一盔一带”安全守护行动在全国各地积极开展,道路上不戴头盔骑行的现象得到了极大的改善,七七超市的某品牌头盔的销量逐月攀升,已知4月份销售150个,6月份销售216个,且从4月份到6月份销售量的月增长率相同.(1)、求该品牌头盔销售量的月平均增长率;(2)、若此头盔的进价为30元/个,经测算当售价为40元/个时,月销售量为300个;售价每上涨1元,则月销售量减少10个,为使月销售利润达到3960元,并尽可能让顾客得到实惠,则该品牌头盔的售价应定为多少元/个?20. 如图1,在中,的角平分线交边于点 , 甲、乙两人想作菱形 , 使得、两点分别在边和边上,他们的作法如下:甲:作的中垂线分别交、于点、 , 连接、 , 则四边形即为所求;乙:分别作交边于点 , 交于点 , 则四边形即为所求. (1)、对于两人的作法,你认为: ▲
(1)、对于两人的作法,你认为: ▲(A)甲、乙都对;(B)甲、乙都错;(C)甲正确,乙错误;(D)甲错误、乙正确;
请你选择一种甲或乙中你认为正确的作法进行证明(作图无须用尺规);
(2)、如图2,菱形中,过点作 , 垂足为点 , 若点是的中点, , 求的长.21. 小学阶段,我们了解到圆:平面上到定点的距离等于定长的所有的点组成的图形叫做圆。在一节数学实践活动课上,老师手拿着三个正方形硬纸板和几个不同的圆形的盘子,他向同学们提出了这样一个问题:已知手中圆盘的直径为 , 手中的三个正方形硬纸板的边长均为 , 若将三个正方形纸板不重叠地放在桌面上,能否用这个圆盘将其盖住?问题提出后,同学们七嘴八舌,经过讨论,大家得出了一致性的结论是:本题实际上是求在不同情况下将三个正方形硬纸板无重叠地适当放置,圆盘能盖住时的最小直径.然后将各种情形下的直径值与进行比较,若小于或等于就能盖住,反之,则不能盖住.老师把同学们探索性画出的四类图形画在黑板上,如图所示. (1)、通过计算,在图1中圆盘刚好能盖住正方形纸板的最小直径应为.(填准确数(2)、图2能盖住三个正方形硬纸板所需的圆盘最小直径为 , 图3能盖住三个正方形硬纸板所需的圆盘最小直径为.(填准确数)(3)、拓展:按图4中的放置,三个正方形放置后为轴对称图形,当圆心落在边上时,圆的直径是多少,请你写出该种情况下求圆盘最小直径的过程,并判断是否能盖住.(计算中可能用到的数据,为了计算方便,本问在计算过程中,根据实际情况最后的结果可对个别数据取整数)22. 【温故知新】在证明“三角形的中位线平行于第三边,且等于第三边的一半”时,小明结合图1给出如下证明思路:作交的延长线于点 , 再证 , 再证四边形是平行四边形,即可证明定理。
(1)、通过计算,在图1中圆盘刚好能盖住正方形纸板的最小直径应为.(填准确数(2)、图2能盖住三个正方形硬纸板所需的圆盘最小直径为 , 图3能盖住三个正方形硬纸板所需的圆盘最小直径为.(填准确数)(3)、拓展:按图4中的放置,三个正方形放置后为轴对称图形,当圆心落在边上时,圆的直径是多少,请你写出该种情况下求圆盘最小直径的过程,并判断是否能盖住.(计算中可能用到的数据,为了计算方便,本问在计算过程中,根据实际情况最后的结果可对个别数据取整数)22. 【温故知新】在证明“三角形的中位线平行于第三边,且等于第三边的一半”时,小明结合图1给出如下证明思路:作交的延长线于点 , 再证 , 再证四边形是平行四边形,即可证明定理。
图1 图2 图3 图4
(1)、【新知体验】小明思考后发现:作平行线可以构成全等三角形或平行四边形,以达到解决问题的目的.如图2,在四边形中, , , 若 , , , 则的值为(2)、【灵活运用】如图3,在矩形和中,连接、交于点 , 连接。若 , 求的度数;(3)、【拓展延伸】如图4在第(2)题的条件下,连接 , 若 , 求的面积