人教版（贵州地区）初中数学2023-2024学年七年级上学期期末模拟卷（一）

试卷更新日期：2023-12-07 类型：期末考试

进入出卷网下载

一、选择题

1. 下列各数中，负整数是（　　）

A、3 B、-2.1 C、0 D、-7

查看试题解析
2. 某年某月某日，我国神舟十六号飞船发射成功，神舟十六号飞船身高9米，重约8吨，飞行速度约每秒7800米，请将数7800用科学记数法表示为（）

A、0.78×10⁴ B、7.8×10⁴ C、7.8×10³ D、0.78×10³

查看试题解析
3. 下列各式是一元一次方程的是（）

A、2x＝5+3y B、y²＝y+4 C、3x+2＝1-x D、 $x + \frac{1}{x} = 2$

查看试题解析
4. 开学整理教室时，老师总是先把每一列最前和最后的课桌摆好，然后再依次摆中间的课桌，一会儿一列课桌摆在一条线上，整整齐齐，这是因为（）

A、两点之间，线段最短 B、经过一点有无数条直线 C、两点确定一条直线 D、两点之间线段的长度，叫做这两点之间的距离

查看试题解析
5. 下列运算结果正确的是（）

A、5x-x=5 B、2x²+2x³=4x⁵ C、-n²-n²=-2n² D、a²b-ab²=0

查看试题解析
6. 已知a，b两数在数轴上对应的位置如图所示，则下列结论正确的是（）

A、a+b>0 B、a-b>0 C、|a|>|b| D、ab<0

查看试题解析
7. 把方程 $\frac{2 x - 1}{4} = 1 - \frac{3 - x}{8}$ 作去分母变形，结果正确的是（）

A、2x-1=1-(3-x) B、2(2x-1)=1-(3-x) C、2(2x-1)=8-3-x D、2(2x-1)=8-(3-x)

查看试题解析
8. 单项式-x³y^m与2xⁿy⁴是同类项，则m+n的值为（　　）

A、7 B、-7 C、5 D、-5

查看试题解析
9. 一项工程甲单独做需20天完成，乙单独做需30天完成，甲先单独做5天，然后甲、乙两人合作x天完成这项工程，则下面所列方程正确的是（）

A、 $\frac{5}{20} + \frac{x}{20 + 30}$ =1 B、 $\frac{5}{20} + \frac{x}{20 \times 30}$ =1 C、 $\frac{5}{20} + \frac{x}{30}$ =1 D、 $\frac{5 + x}{20} + \frac{x}{30}$ =1

查看试题解析
10. 一只跳蚤在数轴上从原点O开始沿数轴左右跳动，第1次向右跳1个单位长度，第2次向左跳2个单位长度，第3次向右跳3个单位长度，第4次向左跳4个单位长度，…，依此规律跳下去，当它第2023次落下时，落点处对应的数为（）

A、-1012 B、1012 C、-2023 D、2023

查看试题解析

二、填空题

11. 请写出一个比 $- 3.1$ 大的负整数是．（写出一个即可）

查看试题解析
12. 若∠1=75°，则∠1的补角的大小为

查看试题解析
13. 关于 $x$ 的一元一次方程 $2 x^{a + 2} + m = 4$ 的解为 $x = 1$ ，则 $a^{m}$ 的值为．

查看试题解析
14. 某商场以每件 $200$ 元的价格购进一批秋季夹克衫，由于季节突变导致滞销，于是商场决定在标价基础上打八折销售，每件夹克衫仍可获利 $20 %$ ，则该夹克衫的标价为元.

查看试题解析
15. 有一无弹性细线，拉直时测得细线 $O P$ 长为 $8 cm$ ，现进行如下操作：1.在细线上任取一点 $A$ ；2.将细线折叠，使点 $O$ 与点 $A$ 重合，记折点为点 $B$ ；3.将细线折叠，使点 $P$ 与点 $A$ 重合，记折点为点 $C$ .

(1)、如图， $B C$ 的长为 $cm$ ；

(2)、继续进行折叠，使点 $B$ 与点 $C$ 重合，并把 $B$ 点和与其重叠的 $C$ 点处的细线剪开，使细线分成长为 $a$ ， $b$ ， $c$ 的三段 $(a < b < c)$ ，当 $a ： b = 1 ： 3$ ，则细线未剪开时 $O A$ 的长为 $cm$ .

查看试题解析

三、计算题

16. 计算：

(1)、0.6- $\frac{1}{4}$ -（-3.75）+ $\frac{2}{5}$

(2)、 $(- \frac{2}{5}) + (- 3 \frac{4}{7}) - 1.6 - (- \frac{11}{7})$

查看试题解析
17. 计算：

(1)、 $(- 3) \times (- 4) - 60 \div (- 12)$ ；

(2)、 $4 + (- 2)^{2} \times 2 - (- 36) \div 4$ ；

(3)、 $- (- 5)^{2} - (- 2)^{3} + (1 - 0.8 \times \frac{3}{4}) \div (- 2)$ ．

查看试题解析
18. 解方程：

(1)、3x-9=6x-1．

(2)、 $x - \frac{x - 1}{4} = 1 - \frac{3 - x}{2}$

查看试题解析

四、解答题

19. 有理数a ， b ， c在数轴上的位置如图所示．

(1)、由图可得：a－c0，a－b0，b－c0（填＜，＞，＝）；

(2)、结合（1）化简： $| a - c | + | a - b | - | b - c |$ ．

查看试题解析

五、综合题

20. 如图是一个正方体纸盒的展开图，已知这个正方体纸盒相对两个面上的代数式的值相等．

(1)、求 $a$ ， $b$ ， $c$ 的值；

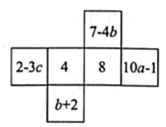(2)、求代数式 $b c - [2 a b - (3 a b c - b c) + 4 a b c]$ 的值．

查看试题解析
21. 某文艺团体为“希望工程”募捐组织了一场义演，共售出1000张票，筹出票款6920元，且每张成人票8元，学生票5元.

(1)、问成人票与学生票各售出多少张？

(2)、若票价不变，仍售出1000张票，所得的票款可能是7290元吗？为什么？

查看试题解析
22. 卡塔尔世界杯的举办掀起了青少年校园足球热，某体育用品商店对甲、乙两种品牌足球开展促销活动，已知甲、乙两种品牌足球的标价分别是：160元/个，60元/个，现有如下两种优惠方案：
方案一：不办理会员卡，购买甲种品牌足球享受8.5折优惠；购买乙种品牌足球，5个（含5个）以上享受8.5折优惠，5个以下按标价购买．

方案二：办理一张会员卡100元，购买甲、乙两种品牌足球均享受7.5折优惠．

(1)、若购买甲种品牌足球3个，乙种品牌足球4个，哪一种方案更优惠？多优惠多少元？

(2)、若购买甲种品牌足球若干个，乙种品牌足球6个，方案一与方案二所付金额相同，求购买甲种品牌的足球个数．

查看试题解析
23. 如图，点 $C$ 是线段 $A B$ 上一点，并且 $A C ： C B = 1 ： 2$ ，点 $M$ ， $N$ 分别为 $A C$ ， $C B$ 的中点.

(1)、若线段 $A B = 24 c m$ ，求 $B C - A C$ 的值；

(2)、若线段 $A B = a c m$ ，求线段 $M N$ 的长.（用含 $a$ 的式子表示）

查看试题解析
24. 如图，P是线段AB上一点，AB＝18cm，C，D两动点分别从点P，B同时出发沿射线BA向左运动，到达点A处即停止运动.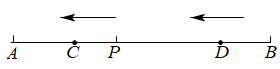

(1)、若点C，D的速度分别是1cm/s，2cm/s.
①当动点C，D运动了2s，且点D仍在线段PB上时，AC＋PD＝cm；
②若点C到达AP中点时，点D也刚好到达BP的中点，则AP∶PB＝；

(2)、若动点C，D的速度分别是1cm/s，3cm/s，点C，D在运动时，总有PD＝3AC，求AP的长度.

查看试题解析

六、实践探究题

25. 如图1，O是直线AB上的一点，OC⊥OD ， OE平分∠BOC ．

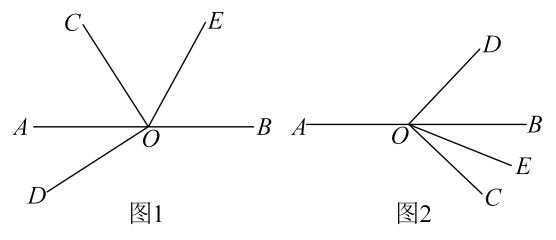(1)、若∠AOD＝35°，求∠BOE的度数；

(2)、将图1中的∠DOC绕顶点O顺时针旋转至图2的位置．
①探究∠AOC和∠DOE的度数之间的关系，并说明理由；
②在∠AOC的内部有一条射线OF ， ∠BOE内部有一条射线OM ，且3∠AOD－∠AOF＋2∠MOE＝13∠COE＋∠AOF ，试确定∠FOM与∠DOE的度数之间的关系，并说明理由．

查看试题解析