新高考四大基础题(三角+数列+立体几何+概率)一天两题--专练5
试卷更新日期:2023-12-06 类型:二轮复习
一、作业1
-
1. 已知的内角A,B,C的对边分别为a,b,c, .(1)、证明:为定值;(2)、若 , , 求的周长.2. 已知为数列的前项和, , .(1)、求;(2)、若 , 证明: .
二、作业2
-
3. 青少年近视问题备受社会各界广泛关注,某研究机构为了解学生对预防近视知识的掌握程度,对某校学生进行问卷调查,并随机抽取200份问卷,发现其得分(满分:100分)都在区间中,并将数据分组,制成如下频率分布表:
分数
频率
0.15
0.25
0.30
0.10
(1)、试估计这200份问卷得分的平均值(同一组中的数据用该组区间的中点值代表);(2)、用样本估计总体,用频率估计概率,从该校学生中随机抽取4人深入调查,设X为抽取的4人中得分在的人数,求的分布列与数学期望.4. 在四棱锥中,底面 , , , , , .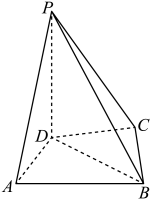 (1)、证明:平面平面;(2)、若 , 求二面角的余弦值.
(1)、证明:平面平面;(2)、若 , 求二面角的余弦值.三、作业3
-
5. 在中,内角A,B,C的对边分别为a,b,c,且 .(1)、求C;(2)、若 , 求 .6. 已知数列的前n项和为 , , 且 .(1)、求证:数列为等差数列;(2)、若 , 求数列的前n项和 .
四、作业4
-
7. 某大型国有企业计划在某双一流大学进行招聘面试,面试共分两轮,且第一轮通过后才能进入第二轮面试,两轮均通过方可录用.甲、乙、丙、丁4名同学参加面试,已知这4人面试第一轮通过的概率分别为 , , , , 面试笫二轮通过的概率分别为 , , , , 且4人的面试结果相互独立.(1)、求甲、乙、丙、丁4人中至少有1人被录用的概率;(2)、记甲、乙、丙、丁4人中最终被录用的人数为X,求X的分布列和数学期望.8. 如图,在四棱锥中,四边形为梯形, , , , 为正三角形, , , O为的中点.
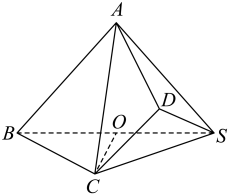 (1)、求证;平面;(2)、求二面角的余弦值.
(1)、求证;平面;(2)、求二面角的余弦值.五、作业5
-
9. 小明同学参加了本次数学质检测验,在做选择题时(每题5分),前9道题均会做,但由于粗心做错一题,后3题不会做,只好每题从四个选项中随机蒙了一个.(1)、求小明同学选择题得分不低于50分的概率;(2)、当小明同学完成填空题时,考试时间只剩55分钟,此时还需完成6道解答题.若根据小明同学近期几次模拟考时一道解答题平均所需花费时间估计概率(下表所示)
一题所需时长/分钟
8
9
10
概率
0.5
以小明同学答题时间的期望为依据,预计小明同学这次质检能顺利完成所有题目,求 的取值范围.
10. 已知数列 满足:奇数项 组成的数列 为等差数列;偶数项 组成的数列 为等比数列,且 .(1)、求 ;(2)、求 的前20项和 .六、作业6