2023-2024学年北师大版数学八年级上册 6.4数据的离散程度 同步练习（培优卷）

试卷更新日期：2023-12-06 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 为迎接中国共产党建党101周年，某班40名同学进行了党史知识竞赛，测试成绩统计表如下，其中有两个数据被遮盖．下列关于成绩的统计量中，与被遮盖的数据无关的是（ ）

    成绩

    91

    92

    93

    94

    95

    96

    97

    98

    99

    100

    人数

    1

    3

    2

    3

    5

    5

    8

    10

    ■

    ■

    A、平均数，方差 B、中位数，方差 C、平均数，众数 D、中位数，众数

    查看试题解析

  • 2. 一组数据的方差计算公式为：s2=14[(6−x¯)2+(6−x¯)2+(7−x¯)2+(9−x¯)2] ， 下列关于这组数据的说法错误的是（ ）
    A、平均数是7 B、中位数是6.5 C、众数是6 D、方差是1

    查看试题解析

  • 3. 在一次射击比赛中，甲、乙两名运动员10次射击的平均成绩都是9环，其中甲成绩的方差为1.21，乙成绩的方差为3.98，由此可知（ ） 
    A、甲比乙的成绩稳定 B、乙比甲的成绩稳定 C、甲、乙两人的成绩一样稳定 D、无法确定谁的成绩更稳定

    查看试题解析

  • 4. 如图是甲、乙两名同学五次数学测试成绩的折线图.比较甲、乙两名同学的成绩，下列说法正确的是（ ）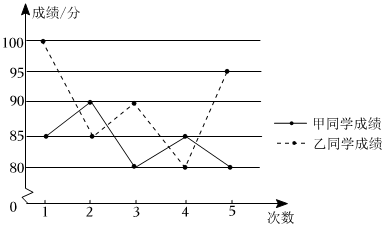

    A、甲同学平均分高，成绩波动较小 B、甲同学平均分高，成绩波动较大
     C、乙同学平均分高，成绩波动较小 D、乙同学平均分高，成绩波动较大

    查看试题解析

  • 5. 初中三年学习生涯，让懵懂青涩的少年逐渐成长为奋发向上的青年．比较九(1)班50名同学三年前后的年龄数据，在平均数、众数、中位数和方差四个统计量中，大小没有发生变化的统计量是（ ）
    A、平均数 B、众数 C、中位数 D、方差

    查看试题解析

  • 6. 下列说法正确的是（ ）
    A、调查红塔区中小学生的视力情况，应该采用全面调查的方式
     B、一组数据2 ， 0 ， 2 ， 3 ， 2 ， 1的众数和平均数都是2 C、抛掷一枚质地均匀的硬币1000次，一定有500次正面向上 D、甲、乙两个班级参加体育艺术节的开幕式，若甲、乙两个班级学生身高的平均数相同，方差分别是S甲2=0.41 ， S乙2=2.9 ， 则甲班级学生的身高较乙班级学生的身高更整齐

    查看试题解析

  • 7. 我校《足球》社团有30名成员，下表是社团成员的年龄分布统计表，对于不同的x ， 下列关于年龄的统计量不会发生改变的是（ ）                                                                                                                           

    年龄(单位：岁)

             11

             12

             13

             14

             15

    频数(单位：名)

             5

             12

             x

             11−x

        2

    A、平均数、中位数 B、平均数、方差 C、众数、中位数 D、众数、方差

    查看试题解析

  • 8. 某次比赛中，五位同学答对题目的个数分别为7 ， 5 ， 3 ， 5 ， 10 ， 则关于这组数据的说法正确的是（ ）
    A、方差是3.6 B、众数是10 C、中位数是3 D、平均数是6

    查看试题解析

  • 9. 若一组数据x1+1 ， x2+1 ， ⋯ ， xn+1的平均数为17，方差为2，则另一组数据x1+2 ， x2+2 ， ⋯ ， xn+2的平均数和方差分别为（  ）
    A、17，2 B、17，3 C、18，1 D、18，2

    查看试题解析

  • 10. 一组数据a、b、c、d、e、f、g的平均数是m ， 方差是n ， 则另一组数据2a-3、2b-3、2c-3、2d-3、2e-3、2f-3、2g-3的平均数和方差分别是（　　）
    A、2m、 2n−3 B、2m−3 、n C、m−3 、2n D、2m−3 、4n

    查看试题解析

二、填空题

  • 11.  某射击队要从甲、乙、丙三名队员中选出一人代表射击队参加市里举行的射击比赛，如表是这三名队员在相同条件下10次射击成绩的数据：                                                                                                                                       


    甲

    乙

    丙

    平均数

             8.5

             9

             8.8

    方差

             0.25

             0.23

             0.27

    如果要选出一个成绩好且又稳定的队员去参加比赛，这名队员应是 ．

    查看试题解析

  • 12.  甲、乙两名射击爱好者10次射击测试成绩(单位：环)的统计图如图所示.根据图中的信息，两人中发挥相对稳定的是 ．

    查看试题解析

  • 13. 有一组数据：5，2，a ， 5，2，6，它们的中位数是4.5，则这组数据的方差是.

    查看试题解析

  • 14. 甲、乙两班举行一分钟跳绳比赛，参赛学生每分钟跳绳个数的统计结果如表：                                                                                                                                                           

    班级

    参加人数

    中位数

    方差

    平均数

    甲

    45

    109

    181

    110

    乙

    45

    111

    108

    110

    某同学分析上表后得到如下结论：①甲、乙两班学生平均成绩相同；②乙班优秀人数多于甲班优秀人数(每分钟跳绳≥110个为优秀)；③甲班成绩的波动比乙班大，则正确结论的序号是. 

    查看试题解析

  • 15. 某乳业公司要出口一批规格为500克/罐的奶粉，现有甲、乙两个厂家提供货源，它们的价格相同，品质也相近.质检员从两厂的产品中各随机抽取15罐进行检测，测得它们的平均质量均为500克，质量的折线统计图如图所示，观察图形，甲、乙两个厂家分别提供的15罐奶粉质量的方差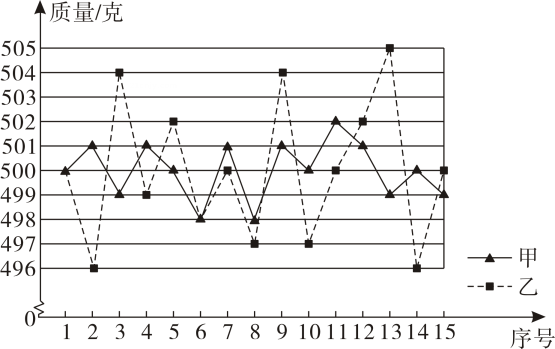s甲2s乙2.(填“>”或“=”或“<”)

    查看试题解析

三、综合题

  • 16. 甲、乙两位同学5次参加“数学学科素养赛”选拔赛的成绩统计如表，他们5次测试的总成绩相同，请同学们完成下列问题：


    第1次

    第2次

    第3次

    第4次

    第5次

    甲成绩

    80

    40

    70

    50

    60

    乙成绩

    70

    50

    70

    a

    70

    (1)、根据统计表求a ， 甲同学成绩的中位数，乙同学成绩的众数；
    (2)、小林计算出甲同学的成绩平均数为60，方差是s2甲=200 ． 请你求出乙同学成绩的平均数和方差；
    (3)、从平均数和方差的角度分析，甲、乙两位同学谁的成绩更稳定．

    查看试题解析

  • 17. 棉花的纤锥长度是棉花质量的重要指标．在甲、乙两类送检的棉花中各随机抽测了20根棉花的纤锥长度（单位：毫米），按从小到大排序结果如下：

    甲：51 ， 54 ， 59 ， 60 ， 64 ， 68 ， 68 ， 68 ， 70 ， 71 ， 72 ， 72 ， 74 ， 76 ， 77 ， 78 ， 79 ， 79 ， 80 ， 80 ．

    乙：51 ， 53 ， 53 ， 56 ， 66 ， 68 ， 68 ， 71 ， 71 ， 71 ， 72 ， 73 ， 73 ， 74 ， 79 ， 80 ， 80 ， 80 ， 80 ， 81 ．

    根据以上数据绘制成统计表：

    名称

    平均数

    众数

    中位数

    方差

    甲

             70

             a

             71.5

             74.84

    乙

             70

             80

             b

             94.84

    (1)、填空：a=；b=；
    (2)、若甲类棉花共有10000根，试估计甲类棉花的纤维长度不低于70毫米的数量；
    (3)、抽检员看了数据及统计表后认为甲类棉花纤维长度的稳定性更好，请结合所学知识和统计数据，写出支持检测员的结论的依据．

    查看试题解析

  • 18. 某中学积极推进校园文学创作，倡导每名学生每学期向校报编辑部至少投1篇稿件．学期末，学校对七、八年级的学生投稿情况进行调查．

    【数据的收集与整理】

    分别从两个年级随机抽取相同数量的学生，统计每人在本学期投稿的篇数，制作了频数分布表．

    投稿篇数（篇）

    1

    2

    3

    4

    5

    七年级频数（人）

    7

    10

    15

    12

    6

    八年级频数（人）

    2

    10

    13

    21

    4

    【数据的描述与分析】

    (1)、求扇形统计图中圆心角α的度数，并补全频数直方图．

      

    (2)、根据频数分布表分别计算有关统计量：

    统计量

    中位数

    众数

    平均数

    方差

    七年级

    3

    3

    x¯

    1.48

    八年级

    m

    n

    3.3

    1.01

    直接写出表格中m、n的值，并求出x¯ ．

    (3)、【数据的应用与评价】

    从中位数、众数、平均数、方差中，任选两个统计量，对七、八年级学生的投稿情况进行比较，并做出评价．

    查看试题解析

  • 19. 为了解甲、乙两个班在数学测试中对某一个解答题的解答情况，分别在两个班随机抽取了20名学生的成绩（满分10分），对其进行整理、描述和分析．下面给出①、②两组信息：

    ①乙班20名学生成绩的条形统计图如图所示：

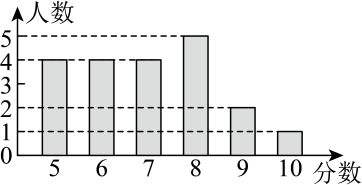
    ②甲、乙两个班所抽取的20名学生成绩的平均数、众数、中位数和方差如下表所示：（单位：分）

    班级

    平均数

    众数

    中位数

    方差

    甲

    7

    7

    7

    S甲2=2.15

    乙

    7

    m

    p

    S乙2

    根据以上信息，解答下列问题：

    (1)、填空：上表中m= ， p=；
    (2)、求上表中S乙2的值，并用样本估计总体的方法分析哪个班学生的成绩表现更稳定？

    查看试题解析

  • 20.  我校在七、八年级举行了“新冠疫情防控”知识竞赛，从七、八年级各随机抽取了10名学生进行比赛（百分制）．测试成绩整理、描述和分析如下：

    成绩得分用x表示，共分成四组：

    （A）.80≤x<85；（B）85≤x<90；（C）90≤x<95；（D）95≤x≤100 ．

    七年级10名学生的成绩：96 ， 86 ， 96 ， 86 ， 99 ， 96 ， 90 ， 100 ， 89 ， 82 ．

    八年级10名学生的成绩在C组中的数据是：94 ， 90 ， 92 ．

    七、八年级抽取的学生竞赛成绩统计表

                                                                                                                                                               

    年级

    平均数

    中位数

    众数

    方差

    七年级

             92

             b

             c

             d

    八年级

             92

             93

             100

             50.4

    根据以上信息，解答下列问题：

    (1)、a= ， b= ， c= ．
    (2)、这次比赛中哪个年级成绩更稳定？说明理由．
    (3)、我校八年级共800人参加了此次活动，估计参加此次活动成绩优秀(x≥90)的八年级学生人数是多少？

    查看试题解析