2023-2024学年北师大版数学八年级上册 6.3从统计图分析数据的集中趋势同步练习（培优卷）

试卷更新日期：2023-12-06 类型：同步测试

进入出卷网下载

一、选择题

1. 甲、乙、丙、丁四名射击运动员进行射击测试，每人10次射击成绩的平均数 $\bar{x}$ （单位：环）及方差S²（单位：环）如表所示：根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择（　　）

甲
乙
丙
丁
$\bar{x}$
9
8
9
9
S²
1.8
0.6
5
0.6

A、甲 B、乙 C、丙 D、丁

查看试题解析

2. “多读书，读好书”是提升学生阅读能力的重要举措，某校倡议学生在家多读一些教育部推荐的中外名著，王老师为了解学生每周在家阅读中外名著的时间，随机调查了本班20名学生，收集到如下数据：

时间（小时）	6	5	4	3	2
人数（人）	2	6	4	6	2

关于每周在家阅读中外名著的时间的描述，正确的是（）

A、众数是6 B、平均数是4 C、中位数是3 D、方差是1

查看试题解析

3. 某射击队计划从甲、乙、丙、丁四名运动员中选拔一人参加国际射击比赛，在选拔过程中，每人射击10次，计算他们的平均成绩及方差如下表所示：

	甲	乙	丙	丁
$\bar{x}$ /环	9.6	9.6	9.7	9.7
$s^{2}$	0.015	0.042	0.015	0.042

射击队决定依据他们的平均成绩及稳定性进行选拔，那么被选中的运动员是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

4. 为贯彻落实教育部办公厅关于“保障学生每天校内、校外各1小时体育活动时间”的要求，学校要求学生每天坚持体育锻炼．小亮记录了自己一周内每天校外锻炼的时间（单位：分钟），并制作了如图所示的统计图．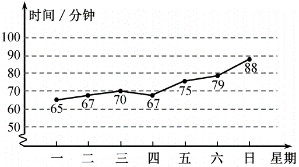

根据统计图，下列关于小亮该周每天校外锻炼时间的描述，正确的是（）

A、平均数为70分钟 B、众数为67分钟 C、中位数为67分钟 D、方差为0

查看试题解析
5. 一次数学测试，甲、乙两班同学的成绩统计并分析如图所示，则下列说法正确的是（）

参加人数
平均数
中位数
方差
甲
50
85
83
5.1
乙
50
85
85
4.6

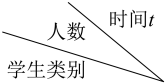
A、甲班的成绩比乙班的成绩稳定 B、小明得84分将排在甲班的前25名 C、甲，乙两班竞赛成绩的众数相同 D、甲班的整体成绩比乙班好

查看试题解析
6. 甲、乙两人在相同的条件下各射击10次，将每次命中的环数绘制成如图所示统计图．根据统计图得出的结论正确的是（）

A、甲的射击成绩比乙的射击成绩更稳定 B、甲射击成绩的众数大于乙射击成绩的众数 C、甲射击成绩的平均数大于乙射击成绩的平均数 D、甲射击成绩的中位数大于乙射击成绩的中位数

查看试题解析
7. 某校共有200名学生．为了解本学期学生参加公益劳动的情况，收集了他们参加公益劳动时间（单位：小时）等数据．下图是根据数据绘制的统计图表的一部分．下面有四个推断：
①这200名学生参加公益劳动时间的平均数一定在 $24.5 \sim 25.5$ 之间；②这200名学生参加公益劳动时间的中位数在 $20 ∼ 30$ 之间；③这200名学生中的初中生参加公益劳动时间的中位数一定在 $20 ∼ 30$ 之间；④这200名学生中的高中生参加公益劳动时间的中位数可能在 $20 ∼ 30$ 之间．
所有合理推断的序号是（）
$0 \leq t < 10$
$10 \leq t < 20$
$20 \leq t < 30$
$30 \leq t < 40$
$t \geq 40$
性别
男
7
31
25
30
4
女
8
29
26
32
8
学段
初中
25
36
44
11
高中

A、①③ B、②④ C、①②③ D、①②③④

查看试题解析
8. 如图是某班去年1～8月份全班同学每月的课外阅读数量折线统计图，下列说法正确的是（）

A、每月阅读数量的中位数是58 B、每月阅读数量的众数是83 C、每月阅读数量的平均数是50 D、每月阅读数量的极差是65

查看试题解析
9. 某地2022年6月上半个月日最高气温统计图、表如下：

日最高温度（℃）

天数

27

4

28

4

29

2

30

3

32

2

则计算这半个月平均最高气温的算式错误的是（）

A、 $(28 + 29 + 30 + 32 + 32 + 30 + 28 + 27 + 30 + 29 + 28 + 27 + 28 + 27 + 27) \div 15$ B、 $(27 + 28 + 29 + 30 + 32) \div 5$ C、 $[27 \times 4 + 28 \times 4 + 29 \times 2 + 30 \times 3 + 32 \times 2] \div 15$ D、 $[(27 + 28) \times 4 + (29 + 32) \times 2 + 30 \times 3] \div 15$

查看试题解析
10. 某中学积极响应党的号召，大力开展各项有益于德智体美劳全面发展的活动小明同学在某学期德智体美劳的评价得分如图所示，则小明同学五项评价的平均得分为（）

A、7分 B、8分 C、9分 D、10分

查看试题解析

二、填空题

11. 甲、乙、丙、丁四名射击队员考核赛的平均成绩（环）及方差统计如表，现要根据这些数据，从中选出一人参加比赛，如果你是教练员，你的选择是．
队员
平均成绩（环）
方差
甲
9.7
2.12
乙
9.6
0.56
丙
9.7
0.56
丁
9.6
1.34

查看试题解析

12. 两台A、B型号的大米自动封装机包装的质量为

50 k m

的袋食品中各封装了10袋大米，测得其实际质量如下表（单位：

k m

）：

A	$50.1$	$\begin{array}{l} 50.6 \end{array}$	$\begin{array}{l} 50.8 \end{array}$	$49.7$	$\begin{array}{l} 50.8 \end{array}$	$49.6$	$50.5$	$50.3$	$\begin{array}{l} 49.5 \end{array}$	$\begin{array}{l} 49.9 \end{array}$
B	$50.5$	$\begin{array}{l} 50.2 \end{array}$	$\begin{array}{l} 49.8 \end{array}$	$50.1$	$\begin{array}{l} 49.9 \end{array}$	$50.3$	$\begin{array}{l} 49.8 \end{array}$	$\begin{array}{l} 50.2 \end{array}$	$50.1$	$\begin{array}{l} 49.9 \end{array}$

由上表可以判断型号自动封装机性能更好．

查看试题解析

13. 质检部门从甲，乙两个厂家生产的同一种产品中，各抽出8件产品，对其使用寿命进行跟踪调查，结果如下（单位：年）
甲：3，4，5，6，7，7，8，8；乙：4，6，6，6，8，9，12，13．
已知两个厂家在广告中都称该种产品的使用寿命是6年．请根据调查结果判断厂家在广告中分别运用了平均数、众数、中位数中哪一种特征数？
甲：，乙：．

查看试题解析
14. 寒假期间，滑雪冬令营的同学们都参加了“单板滑雪”这个项目的40次的训练测试，每次测试成绩分别为5分，4分，3分，2分，1分五档，甲、乙两位同学在这个项目的测试成绩统计结果如图所示：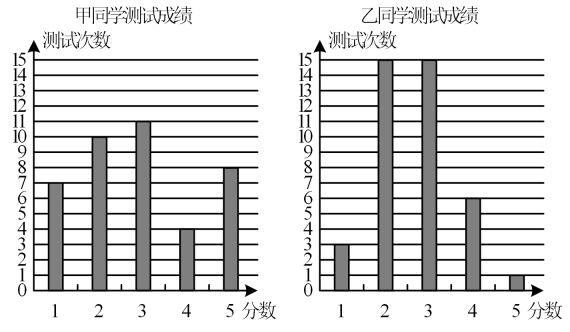
结合图中数据，请你从平均数、众数、中位数、方差中选择一方面评论一下两位同学的滑雪成绩．

查看试题解析
15. 现有1，2，3，…，9九个数字，甲、乙轮流从中选出一个数字，从左至右依次填入下图所示的表格中（表中已出现的数字不再重复使用），每次填数时，甲会选择填入后使表中现有数据平均数最大的数字，乙会选择填入后使表中现有数据中位数最小的数字．如图，若表中第一个数字是4，甲先填，则满足条件的填法有种，请你在表中空白处填出一种符合要求的填数结果．

4

查看试题解析

三、综合题

16. 甲、乙两位同学5次参加“数学学科素养赛”选拔赛的成绩统计如表，他们5次测试的总成绩相同，请同学们完成下列问题：

第1次
第2次
第3次
第4次
第5次
甲成绩
80
40
70
50
60
乙成绩
70
50
70
$a$
70

(1)、根据统计表求 $a$ ，甲同学成绩的中位数，乙同学成绩的众数；

(2)、小林计算出甲同学的成绩平均数为60，方差是 ${s^{2}}_{甲} = 200$ ．请你求出乙同学成绩的平均数和方差；

(3)、从平均数和方差的角度分析，甲、乙两位同学谁的成绩更稳定．

查看试题解析

17. 某校为了了解初一年级共480名同学对环保知识的掌握情况，对他们进行了环保知识测试．现随机抽取甲、乙两班各15名同学的测试成绩（满分100分）进行整理分析，过程如下：

【收集数据】

甲班15名学生测试成绩分别为：78，83，85，87，89，90，92，93，94，96，97，98，99，100，100

乙班15名学生测试成绩中 $80 \leq x < 95$ 的成绩如下：90，91，92，93，94

【整理数据】：

班级	$75 \leq x < 80$	$80 \leq x < 85$	$85 \leq x < 90$	$90 \leq x < 95$	$95 \leq x < 100$
甲	1	1	3	4	6
乙	1	2	3	5	4

【分析数据】：

班级	平均数	众数	中位数	方差
甲	92	$a$	93	47.3
乙	90	87	$b$	50.2

【应用数据】：

(1)、根据以上信息，填空：

a =

，

b =

；

(2)、若规定测试成绩92分及其以上为优秀，请估计参加环保知识测试的480名学生中成绩为优秀的学生共有多少人？

(3)、根据以上数据，你认为哪个班的学生环保知识测试的整体成绩较好？请说明理由（一条理由即可）．

查看试题解析

18. 某校为了改善学生伙食，准备午餐为学生提供鸡翅，现有A ， B两家副食品厂可以提供规格为75g的鸡翅，而且它们的价格相同，品质也相近，质检人员分别从两家随机各抽取10个，记录它们的质量（单位：g）如下：

A副食品厂：74，74，74，75，73，77，78，72，76，77．

B副食品厂：78，74，77，73，75，75，74，74，75，75．

并对以上数据进行整理如下：

	平均数	中位数	众数	方差
A副食品厂	75	74.5	b	3.4
B副食品厂	75	a	75	2

根据以上分析，回答下列问题：

(1)、统计表中

a =

，

b =

；

(2)、根据以上信息估计B副食品厂加工的100个鸡翅中，质量为75g的鸡翅有多少个？

(3)、如果只考虑鸡翅质量与规格的匹配程度，学校应该选购哪家副食品厂的鸡翅？说明理由．

查看试题解析

19. 某螺母加工厂为了解工人的日均生产能力，随机调查了一部分工人日均加工螺母的数量、根据调查结果，绘制出如下统计图①和图②．

请根据相关信息，解答下列问题：

(1)、本次接受调查的工人人数为；图①中m的值为；

(2)、求所抽取工人日均加工螺母个数数据的平均数、众数和中位数；

(3)、若该工厂共有加工螺母的工人84人，则日均加工螺母数为16个的约有多少人？

查看试题解析
20. 2022年3月25日，教育部印发《义务教育课程方案和课程标准（2022年版）》，优化了课程设置，将劳动从综合实践活动课程中独立出来.某校为了解该校学生一周的课外劳动情况，随机抽取部分学生调查了他们一周的课外劳动时间，将数据进行整理并制成如下统计图.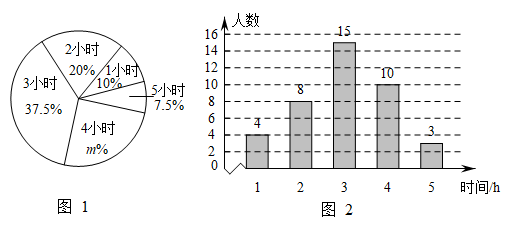
请根据图中提供的信息，解答下面的问题：

(1)、求图1中的m= ，本次调查数据的中位数是h，本次调查数据的众数是h；

(2)、该校此次抽查的这些学生一周平均的课外劳动时间是多少？

(3)、若该校共有2000名学生，请根据统计数据，估计该校学生一周的课外劳动时间不小于 $3 h$ 的人数.

查看试题解析

	参加人数	平均数	中位数	方差
甲	50	85	83	5.1
乙	50	85	85	4.6

		$0 \leq t < 10$	$10 \leq t < 20$	$20 \leq t < 30$	$30 \leq t < 40$	$t \geq 40$
性别	男	7	31	25	30	4
性别	女	8	29	26	32	8
学段	初中		25	36	44	11
学段	高中

队员	平均成绩（环）	方差
甲	9.7	2.12
乙	9.6	0.56
丙	9.7	0.56
丁	9.6	1.34

	第1次	第2次	第3次	第4次	第5次
甲成绩	80	40	70	50	60
乙成绩	70	50	70	$a$	70

日最高温度（℃）	天数
27	4
28	4
29	2
30	3
32	2

2023-2024学年北师大版数学八年级上册 6.3从统计图分析数据的集中趋势 同步练习（培优卷）

一、选择题

二、填空题

三、综合题

2023-2024学年北师大版数学八年级上册 6.3从统计图分析数据的集中趋势同步练习（培优卷）