吉林省名校调研卷系列（省命题A）2023-2024学年八年级上学期第三次月考数学试题

试卷更新日期：2023-12-06 类型：月考试卷

进入出卷网下载

一、选择题（每小题 2 分，共 12分）

1. 围棋起源于中国，古代称之为“弈”，至今已有四千多年的历史.下列由黑白棋子摆成的图案是轴对称图形的是（）

A、 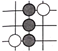B、 C、 D、

查看试题解析
2. 如图，已知AB⊥BD，CD⊥BD，若用“HL”判定 Rt△ABD和Rt△CDB 全等，则需要添加的条件是（）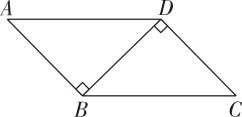

A、AD = CB B、∠A = ∠C C、BD = DB D、AB =CD

查看试题解析
3. 若 $a \cdot a^{m} \cdot a^{2 m + 1} = a^{14} ，$ 则 m的值为（）

A、1 B、2 C、3 D、4

查看试题解析
4. 如图，AD 是△ABC中∠BAC的平分线，DE⊥AB于点E，△ABC的面积为12，DE =2，AB = 7，则 AC 的长是（）

A、3 B、4 C、5 D、6

查看试题解析
5. 下列计算正确的是（）

A、 $x^{3} \cdot 2 x ⁴ = 2 x^{7}$ B、 $x^{6} \div x^{3} = x^{2}$ C、 ${(x^{3})}^{4} = x^{7}$ D、 $x^{2} + x = x^{3}$

查看试题解析
6. 如图是由一副常规直角三角板摆放得到的图形，图中∠ABF 的度数为（）

A、30° B、15° C、60° D、25°

查看试题解析

二、填空题（每小题 3 分，共 24分）

7. 分解因式：2a²+a=.

查看试题解析
8. 已知点 M（1，2）关于 y轴的对称点为点M'，则点 M'的坐标为.

查看试题解析
9. 如图，在四边形 ABCD中，AD∥BC，EF 过BD的中点O，分别交AD和BC于点E、F，若 OE = 2cm，则 OF =cm.

查看试题解析
10. 已知 $a$ 、 $b$ 、 $c$ 是 $△ A B C$ 的三边， $a = 3$ ， $b = 7$ ， $c$ 为整数.则 $c$ 的最小值为.

查看试题解析
11. 若 m+n=2，n-m =-3，则 $n^{2} - m^{2} =$ .

查看试题解析
12. 如图，在△ABC中，边AC的垂直平分线交AC 于点M，交 BC 于点 N，若AB =3，BC=13，那么△ABN 的周长是.

查看试题解析
13. 如图是第四套人民币中的菊花1角硬币，则该硬币边缘镌刻的正九边形的一个外角的度数为.

查看试题解析
14. 若 $x^{2} + (3 - m) x + 25$ 是一个完全平方式，则m的值为.

查看试题解析

三、解答题

15. 计算： $a^{2} \cdot a^{4} + {(- 2 a^{3})}^{2} - a^{7} \div a .$

查看试题解析
16. 如图，E是AC上一点， $B C = C E ， B C + A E = D E ， A B = C D .$ ，求证： $△ A B C ≅ △ D C E .$

查看试题解析
17. 先化简，再求值： ${(x - 2 y)}^{2} - x (x + 3 y) - 4 y^{2} ，$ 其中 $x = - 4 ， y = \frac{1}{2} .$

查看试题解析
18. 如图，AB = BC，∠CDE =120°，DF ∥BA，且 DF 平分∠CDE，求证： $△ A B C$ 是等边三角形.

查看试题解析

四、解答题（每小题7分，共 28 分）

19. 如图，在 $△ A B C$ 中， $∠ C = 90 ° ， ∠ A = 15 ° ，$ ，斜边AB 的垂直平分线交AC于点E，交AB于点 D，AE = 8cm，求 BC 的长.

查看试题解析
20. 如图，在长度为1个单位长度的小正方形组成的网格中，点A、B、C在小正方形的顶点上.

(1)、在图中画出与△ABC关于直线l成轴对称的△A'B'C'；

(2)、在直线 l上找一点Q，使得 BQ = AQ.

查看试题解析
21. 规定“U”“∩”是两种新的运算符号，（ $a \cup b = 10^{a} \times 10^{b} ， a \cap b = 10^{a} \div 10^{b} ，$ 例如： $2 \cup 3 = 10^{2} \times 10^{3} = 10^{5} ； 3 \cap 2 = 10^{3} \div 10^{2} = 10$

(1)、求（2023 ∩2021）的值；

(2)、当x为何值时， $(x \cup 5)$ 的值与 $(23 \cap 17)$ 的值相等.

查看试题解析
22. 如图，在 $△ A C B$ 中， $∠ A C B = 90 ° ， C D ⊥ A B$ 于点D.

(1)、求证： $∠ A C D = ∠ B ；$

(2)、若 AF 平分 $∠ C A B$ 分别交CD、BC于点E、F，求证： $△ C E F$ 是等腰三角形.

查看试题解析

五、解答题（每小题 8 分，共 16 分）

23. 某种植基地有一块长方形和一块正方形实验田，长方形实验田每排种植 $(3 a - b)$ 株豌豆幼苗，种植了（3a+b）排，正方形实验田每排种植（a+b）株豌豆幼苗，种植了 $(a + b)$ 排（a>b>0）.

(1)、长方形实验田比正方形实验田多种植豌豆幼苗多少株？

(2)、当a=4，b=3时，该种植基地这两块实验田一共种植了多少株豌豆幼苗？

查看试题解析

六、解答题（每小题 10分，共 20 分）

24. 【知识生成】
如图①，在边长为a的正方形中剪掉一个边长为b的小正方形 $(a⟩ b ），$ ，把余下的部分剪开拼成一个长方形（如图 ②），图①中阴影部分面积可表示为 $a^{2} - b^{2} ，$ 图②中阴影部分面积可表示为（a+b）（a﹣b），因为两个图中的阴影部分面积是相同的，所以可得到等式： $a^{2} - b^{2} = (a + b) (a - b) .$
【拓展探究】
图③是一个长为2a，宽为2b的长方形，沿图中虚线剪开平均分成四个小长方形，然后按图 ④ 的形状拼成一个正方形，

(1)、用两种不同的方法表示图④中阴影部分的面积：方法1：，方法2：.可得到的等量关系式是；

(2)、若a-b = 5， ab = 3，求 $(a + b)^{2}$ 的值；

(3)、【知识迁移】如图⑤，正方形ABCD 和正方形EFGH 的边长分别为α、b（a>b），若 $a + b = 8 ，$ ab = 5，E 是 AB 的中点，求图中阴影部分的面积和.

查看试题解析
25. 如图，在 $△ A B C$ 中， $A B = A C = 10$ 厘米，BC = 8 厘米，点D为AB的中点，已知点P在线段BC上由点B出发向终点C 运动，同时点 Q在线段CA 上由点C出发向终点A运动.设运动时间为t 秒.

(1)、若点 P 的速度是3 厘米/ 秒，用含t的式子表示线段BP 和CP 的长度；

(2)、若点 P 的速度是3 厘米/ 秒，点Q 的速度是a 厘米/ 秒，且△BPD 和△CPQ恰好全等，求出相对应的 a 和t 的值；

(3)、若点P比点Q的运动速度每秒快1厘米，请直接写出t为何值时，△BPD是以∠B为顶角、 $△ C P Q$ 是以 $∠ C$ 为顶角的等腰三角形.

查看试题解析