吉林省吉林九中2023-2024学年八年级上学期期中数学试卷
试卷更新日期：2023-12-06 类型：期中考试
一、选择题（每小题2分，共12分）
-
1. 下列图形中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 计算（﹣a）3•a2的结果是（ ）A、﹣a6 B、a6 C、﹣a5 D、a53. 若等腰三角形的两条边的长分别为4cm和10cm，则它的周长是（ ）A、14cm B、18cm C、24cm D、18cm或24cm4. 如图，直角三角形被挡住了一部分，小明根据所学知识很快就另外画出了一个与原来完全一样的三角形，这两个三角形全等的依据是（ ）
A、SAS B、ASA C、AAS D、HL5. 若
×4a2b3＝﹣12a3b5c，那么代表的整式是（ ） A、﹣3abc B、﹣3ab2c C、﹣3b2c D、3abc6. 把边长相等的正五边形和正六边形按照如图的方式叠合在一起，AB是正六边形的对角线，则∠α等于（ ）
A、72° B、84° C、88° D、90°二、填空题（每小题3分，共24分）
-
7. 若（x﹣4）0＝1成立，则x应满足的条件是 ．8. 二十边形的外角和等于 ．9. 分解因式：x2﹣9y2＝ ．10. 在△ABC中，AB＝AC＝1cm，当BC＝cm时，△ABC是等边三角形．11. 如图，在中， ， ， 平分的外角 ， 则 ．
12. 若10a＝3，10b＝2，则102a﹣b＝ ．13. 如图，在△ABC中，∠A＝90°，BD平分∠ABC，BC＝12，AD＝4，则△DBC的面积为 ．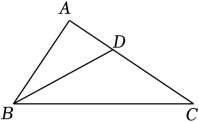
14. 如图，在平面直角坐标系中，点A的坐标为（0，2），点B的坐标为（4，0），在y轴上取一点C使△ABC为等腰三角形，符合条件的C点有 个．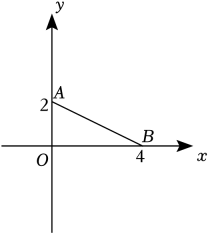
三、解答题（每小题5分，共20分）
-
15. 计算：﹣3x2y2•2xy+（xy）316. 如图，AD是等边三角形ABC的中线，以AD为斜边作等腰直角三角形ADE，求∠EAC的度数．
17. 先化简，再求值：（x﹣2y）2﹣x（x+2y），其中x＝﹣4， ．18. 已知，如图，AD＝BC，AC＝BD，求证：AE＝EB．
四、解答题（每小题7分，共28分）
-
19. 如图，在平面直角坐标系中，△ABC的各顶点坐标分别为A（4，﹣4），B（1，﹣1），C（3，﹣1）．
(1)、画出△ABC关于x轴对称的△A1B1C1；(2)、直接写出点A的对应点A1的坐标．20. 如图，在△ABC中，AB＝AC，∠A＝36°，AC的垂直平分线DE分别交AB，AC于点D，E.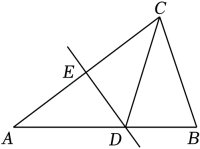
(1)、求证：△BCD是等腰三角形；(2)、若△BCD的周长是13，BC＝5，求AC的长.21. 小刚同学计算一道整式乘法：（3x+a）（2x+3），由于他抄错了多项式中a前面的符号，把“+”写成“﹣”，得到的结果为6x2+bx﹣6．(1)、求a，b的值；(2)、计算这道整式乘法的正确结果．22. 如图，在△ABC中，∠ACB＝90°，∠A＝30°，AB的垂直平分线分别交AB和AC于点D，E．
(1)、求证：AE＝2CE；(2)、连接CD，请判断△BCD的形状，并说明理由．五、解答题（每小题8分，共16分）
-
23. 如图，某小区内有一块长为（3a﹣b）米、宽为（2a+b）米的长方形地块，物业人员计划在中间留一块边长为（a+b）米的正方形地块修建一座假山，然后将剩余阴影部分进行绿化．
(1)、求绿化部分的面积（用含a、b的式子表示）；(2)、当a＝3，b＝1时，求绿化部分的面积．24. 如图
(1)、问题发现如图1，把一块三角板（AB＝BC，∠ABC＝90°）放入一个“U”形槽中，使三角形的三个顶点A、B、C分别在槽的两壁及底边上滑动，已知∠D＝∠E＝90°，在滑动过程中，发现与∠DAB始终相等的角是 ， 与线段AD相等的线段是 ；
(2)、拓展探究如图2，在△ABC中，点D在边BC上，并且DA＝DE，∠B＝∠ADE＝∠C．求证：△ADB≌△DEC．
(3)、能力提升如图3，在等边△DEF中，A，C分别为DE、DF边上的点，AE＝4，连接AC，以AC为边在△DEF内作等边△ABC，连接BF，当∠CFB＝30°时，请直接写出CD的长度．
六、解答题（每小题10分，共20分）
-
25. 【知识生成】通过第14章的学习，我们已经知道，对于一个图形，通过不同的方法计算图形的面积可以得到一个数学等式，请结合图形解答下列问题：
(1)、写出图1中所表示的数学等式 ；(2)、如图2是用4块完全相同的长方形拼成的正方形，用两种不同的方法求图中阴影部分的面积，得到的数学等式是 ；(3)、【知识应用】
若x+y＝7， ， 求x﹣y的值；(4)、【拓展提升】
图3中有两个正方形A、B，现将B放在A的内部得到图甲，将A、B并列放置（无重叠）后构造新的正方形得到图乙．若图甲和图乙中阴影部分的面积分别为2和11，则正方形A、B的面积之和是 ．26. 如图1，已知△ABC是边长为3cm的等边三角形，动点P从点A出发，沿AB边匀速运动；同时，动点Q从点B出发，沿BC边匀速运动．它们的速度都是1cm/s，当点P到达点B时，P、Q两点都停止运动，设点P的运动时间为t（s）．
(1)、BQ的长为 cm，BP的长为 cm（用含t的式子表示）；(2)、求当t为何值时，△PBQ是直角三角形？(3)、如图2，连接AQ、CP相交于点M，则点P、Q在运动的过程中，∠CMQ的大小会变化吗？若变化，请说明理由；若不变，请求出它的度数．