吉林省长春市九台区二十二中2023-2024学年九年级上学期期中数学试卷

试卷更新日期：2023-12-06 类型：期中考试

进入出卷网下载

一、选择题（本大题共8道题，每题3分，共24分）

1. 方程x²＝﹣2x+8化为一元二次方程的一般形式后，二次项系数、一次项系数、常数项分别是（　　）

A、1，﹣2，8 B、﹣1，2，8 C、1，2，﹣8 D、1，2，8

查看试题解析
2. 下列各式中是最简二次根式的是（）

A、 $\sqrt{8}$ B、 $\sqrt{\frac{1}{2}}$ C、 $\sqrt{0.25}$ D、 $\sqrt{10}$

查看试题解析
3. 用配方法解一元二次方程x²﹣6x+8＝0配方后得到的方程是（　　）

A、（x+6）²＝28 B、（x﹣6）²＝28 C、（x+3）²＝1 D、（x﹣3）²＝1

查看试题解析
4. 下列四条线段中，不能成比例的是（）

A、a=2，b=3，c=4，d=6 B、a=1，b= $\sqrt{2}$ ， c= $\sqrt{3}$ ， d= $\sqrt{6}$ C、a=4，b=5，c=6，d=10 D、a=1，b=2，c= $\sqrt{5}$ ， d=2 $\sqrt{5}$

查看试题解析
5. 已知实数a在数轴上的对应点位置如图，则化简 $| a - 1 | - \sqrt{(a - 2)^{2}}$ 的结果是（　　）

A、2a﹣3 B、﹣1 C、1 D、3﹣2a

查看试题解析
6. 泰勒斯是古希腊时期的思想家，科学家，哲学家，他最早提出了命题的证明．泰勒斯曾通过测量同一时刻标杆的影长，标杆的高度。金字塔的影长，推算出金字塔的高度。这种测量原理，就是我们所学的（）

A、图形的平移 B、图形的旋转 C、图形的轴对称 D、图形的相似

查看试题解析
7.
如图，正方形OABC与正方形ODEF是位似图形，O为位似中心，相似比为1： $\sqrt{2}$ ，点A的坐标为（1，0），则E点的坐标为（　　）

A、（ $\sqrt{2}$ ， 0） B、（ $\frac{3}{2}$ ， $\frac{3}{2}$ ） C、（ $\sqrt{2}$ ， $\sqrt{2}$ ） D、（2，2）

查看试题解析
8. 已知P是反比例函数 $y = \frac{12}{x}$ （x＞0）图象上一点，A是y轴正半轴上一点，且AP⊥BP，AP：BP＝1：3，则点P的坐标为（　　）

A、（3，4） B、（2，6） C、（6，2） D、（4，3）

查看试题解析

二、填空题（本大题共6道题，每题3分，共18分）

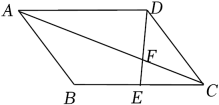
9. 若二次根式 $\sqrt{3 + x}$ 在实数范围内有意义，则 $x$ 的取值范围是 .

查看试题解析
10. 若 $\sqrt{12}$ 与最简二次根式 $\frac{1}{2} \sqrt{a - 1}$ 是同类二次根式，则a的值为

查看试题解析
11. 已知关于x的一元二次方程（a﹣1）x²+a²﹣1=0有一个根为0，则a=

查看试题解析
12. 某玩具商店出售一种“小猪佩奇”玩具，平均每天可销售50个，每个盈利36元，为了尽快减少库存，商场决定采取适当的降价措施，调查发现，若每个玩具降价1元，平均每天可多售出5个，商店要想平均每天销售这种玩具盈利2400元，则每个玩具应降价多少元？设每个玩具应降价x元，可列方程为．

查看试题解析
13. 如图，在平行四边形ABCD中，E是BC的中点，DE，AC相交于点F，S_△CFF＝1，则S_{四边形ABEF}＝．

查看试题解析
14. 在20世纪70年代，我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”，在全国大规模推广，取得了很大成果．如图，利用黄金分割法，所作EF将矩形窗框ABCD分为上下两部分，其中E为边AB的黄金分割点，即BE²＝AE•AB．已知AB为2米，则线段BE的长为米．

查看试题解析

三、解答题（本大题共10道题，共78分）

15. 计算： $\sqrt{8} - 2 \sqrt{18} + \sqrt{24}$ ；

查看试题解析
16. 解方程：x²﹣4x+3＝0．

查看试题解析
17. 如图，四边形ABCD∽四边形EFGH．若AB＝18，EF＝4，FG＝6，∠B＝77°，∠C＝83°，∠E＝117°，求线段BC的长和∠H的大小．

查看试题解析
18. 如图，已知AD•AC＝AB•AE ， ∠DAE＝∠BAC ．求证：△DAB∽△EAC ．

查看试题解析
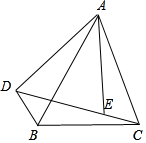19. 截至2017年年末，某市区汽车保有量约为100万辆，预计到2019年年末市区汽车保有量将达到121万辆．设这两年的汽车保有量的年平均增长率均相同．求2017年底至2019年底该市市区汽车保有量的年平均增长率．

查看试题解析
20. 图①、图②、图③都是6×6的网格，每个小正方形的顶点称为格点．△ABC顶点A、B、C均在格点上．在图①、图②、图③给定网格中按要求作图，并保留作图痕迹．

(1)、在图①中画出△ABC的BC边上的中线AD．

(2)、在图②中画出△ABC的AB边上确定一点E，使AE＝2BE．

(3)、在图③中画出△AMN，使得△AMN与△ABC是位似图形，且点A为位似中心，点M、N分别在AB、AC边上，位似比为 $\frac{1}{3}$ ．

查看试题解析
21. 关于x的一元二次方程x²+2mx+m²+m＝0有两个不相等的实数根．

(1)、求m的取值范围．

(2)、设出x₁、x₂是方程的两根，且x₁²+x₂²＝12，求m的值．

查看试题解析

22. 【教材呈现】下面是华师版教材九年级上册52页的部分内容：

我们可以发现，当两条直线与一组平行线相交时，所截得的线段存在一定的比例关系： $\frac{A D}{D B} = \frac{F E}{E C}$ ．这就是如下的基本事实：

两条直线被一组平行线所截，所得的对应线段成比例．（简称“平行线分线段成比例”）

(1)、【问题原型】如图①，在矩形ABCD中，点E为边AB的中点，过E作EF∥AD交边DC于点F，点P、Q分别在矩形的边AD、BC上，连结PQ交EF于点M．求证：PM＝QM．

(2)、【结论应用】如图②，在【问题原型】的基础上，点R在边BC上（不与点Q重合），连结PR交EF于点N．
若MN＝4，则线段QR的长为；

(3)、当点Q与点B重合，点R与点C重合时，如图③，若BC＝10，且△PMN周长的最小值为12，则边AB的长为．

查看试题解析

23. 如图1，为美化校园环境，某校计划在一块长为60米，宽为40米的长方形空地上修建一个长方形花圃，并将花圃四周余下的空地修建成同样宽的通道，设通道宽为a米．

(1)、花圃的面积为平方米（用含a的式子表示）；

(2)、如果花所占面积是整个长方形空地面积的 $\frac{5}{8}$ ，求出此时通道的宽；

(3)、已知某园林公司修建通道、花圃的造价y₁（元）、y₂（元）与修建面积x（m²）之间的函数关系如图2所示，如果学校决定由该公司承建此项目，并要求花圃的面积要超过800平方米，那么通道宽为多少时，修建的通道和花圃的总造价为105920元？

查看试题解析
24. 如图，在△ABC中，∠C＝90°，AC＝4，AB＝5，点D为边AB上的点，且BD＝1．动点P从点A出发（点P不与点A、C重合），沿AC以每秒1个单位长度的速度向终点C运动，同时点Q从点C出发，以相同的速度沿折线CB一BD向终点D运动，以DP、DQ为邻边构造▱PEQD，设点P运动的时间为t（0＜t＜4）秒．

(1)、当点Q与点B重合时，t的值为；

(2)、当点E落在AC边上时，求t的值；

(3)、设▱PEQD的面积为S（S＞0），求S与t之间的函数关系式；

(4)、连结PQ，直接写出PQ与△ABC的边平行时t的值．

查看试题解析