吉林省四平市伊通满族自治县2023-2024学年八年级上学期期中数学试题

试卷更新日期：2023-12-06 类型：期中考试

进入出卷网下载

一、单项选择题（每小题3分，共18分）

1. 在以下中国银行、建设银行、工商银行、农业银行图标中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（　　）

A、 $5 a - 2 a = 3 a$ B、 $3 a + 2 b = 5 a b$ C、 $b^{2} \cdot b^{3} = b^{6}$ D、 ${(x + y)}^{2} = x^{2} + y^{2}$

查看试题解析
3. 一个正多边形的每个外角都等于45°，则这个多边形的边数为（）

A、4 B、6 C、8 D、10

查看试题解析
4. 若 ${(x - 1)}^{0} = 1$ 成立，则 $x$ 的取值范围是（）

A、 $x = - 1$ B、 $x \neq 1$ C、 $x = 1$ D、 $x \neq 0$

查看试题解析
5. 下列长度的三条线段能组成三角形的是（）

A、3，4，8 B、 $3 a$ ， $3 a$ ， $6 a (a > 0)$ C、4，5，9 D、4，5，8

查看试题解析
6. 如图所示，点D在线段BC的延长线上， $D E ⊥ A B$ 于点E，交AC于点F.如果 $∠ A = 35 °$ ， $∠ D = 15 °$ ，则 $∠ A C B$ 的度数为（）

A、60° B、70° C、75° D、80°

查看试题解析

二、填空题（每小题4分，共32分）

7. 因式分解： $x^{2} - 2 x y + y^{2} =$ .

查看试题解析
8. 若约定 $a \otimes b = 1 0^{a} \times 1 0^{b}$ ，如 $2 \otimes 3 = 1 0^{2} \times 1 0^{3} = 1 0^{5}$ ，则 $3 \otimes 4$ 等于.

查看试题解析
9. 若 $a^{m} = 6$ ， $a^{n} = 9$ ，则 $a^{2 m - n} =$ .

查看试题解析
10. 点 $A (- 2 ， 4)$ 关于x轴对称点的坐标是.

查看试题解析
11. 已知x+y＝8，xy＝2，则x²y+xy²＝．

查看试题解析
12. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，以点A为圆心，适当的长度为半径画弧，分别交AC、AB于点M、N，再分别以M、N为圆心，以大于 $\frac{1}{2} M N$ 的长度为半径画弧，两弧交于点O，作射线AO交BC于点D，若 $∠ B = 54 °$ ，则 $∠ C D A =$ 度.

查看试题解析
13. 如图，四边形ABCD的对角线AC，BD相交于点O， $△ A B O ≌ △ A D O$ ，下列结论：① $A C ⊥ B D$ ；② $C B = C D$ ；③ $△ A B C ≌ △ A D C$ ；④ $D A = D C$ .其中正确结论的序号是.

查看试题解析
14. 如图，把 $△ A B C$ 的一角折叠，若 $∠ 1 + ∠ 2 = 130 °$ ，则 $∠ A$ 的度数为.

查看试题解析

三、解答题（每小题5分，共20分）

15. 计算： $(x + 3) (x - 1) - x (x - 2) + 1$

查看试题解析
16. 计算： $(6 x^{4} - 8 x^{3}) \div (- 2 x^{2})$

查看试题解析
17. 如图，已知 $∠ A B C = ∠ B A D$ ， $∠ C = ∠ D$ ，求证： $△ A B C ≌ △ B A D$ .

查看试题解析
18. 图①、图②均是4×4的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点叫做格点， $△ A B C$ 的顶点均在格点上，只用无刻度的直尺，在给定的网格中按要求画图，不要求写出画法，保留作图痕迹.
图①图②

(1)、在图①中画 $△ A B C$ 的角平分线BD，标出点D；

(2)、在图②中 $△ A B C$ 的BC边上找到一点E，连接AE，使线段AE将 $△ A B C$ 分成面积相等的两部分.

查看试题解析

四、解答题（每小题7分，共14分）

19. 先化简，再求值 ${(x - 2 y)}^{2} - x (x + 3 y) - 4 y^{2}$ ，其中 $x = - 4 ， y = \frac{1}{2}$ .

查看试题解析
20. 如图，点C在线段AB上， $A D ∥ E B$ ， $A C = B E$ ， $A D = B C$ .
求证： $△ D C E$ 为等腰三角形

查看试题解析

五、解答题（每小题8分，共16分）

21. 如图，在 $△ A B C$ 中，点D是边BC的中点，过点C画直线CE，使 $C E ∥ A B$ ，交AD的延长线于点E.

(1)、求证： $△ A B D ≌ △ E C D$ ；

(2)、若 $A C = 3$ ， $C E = 5$ ， BD的长是偶数，则BD的长为.

查看试题解析
22. 如图，在 $△ A B C$ 中， $∠ B = 47 °$ ， $△ A B C$ 的外角 $∠ D A C$ 和 $∠ A C F$ 的平分线相交于点E.求 $∠ A E C$ 的度数.

查看试题解析

六、解答题（每小题10分，共20分）

23. 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式.以图①中的正方形ABCD为例：
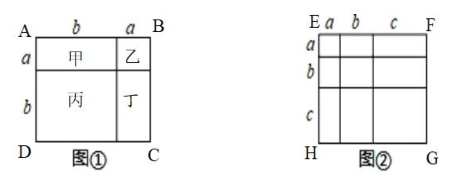
探究：如图①，用含a，b的式子完成以下题目中的（2）和（3）：（1）正方形ABCD的边长为 $a + b$ ，因为正方形的面积等于正方形边长的平方，所以正方形ABCD的面积可以表示为 ${(a + b)}^{2}$ .

(1)、仔细观察图①，正方形ABCD被分割成甲、乙、丙、丁四部分，甲部分的面积为ab，乙部分的面积为 $a^{2}$ ，丙部分的面积为，丁部分的面积为.将这四部分的面积相加就可以得到正方形ABCD的面积为：.

(2)、以上（1）和（2）的探究过程，都表示出了正方形ABCD的面积，从而得到两个数和的平方公式： ${(a + b)}^{2} =$ .

(3)、根据探究的过程，用含有a，b，c的式子表示出由图②中的正方形EFGH可以得到的数学等式：；

(4)、若 $a + b + c = 6$ ， $a^{2} + b^{2} + c^{2} = 14$ ，求 $a b + a c + b c$ 的值；

查看试题解析
24. 如图， $△ A B C$ 是等腰直角三角形， $∠ A C B = 90 °$ ， $A B = 6$ .动点P从点A出发，以每秒2个单位长度的速度在射线AB上运动.点P出发后，连接CP，以CP为直角边向右作等腰直角三角形CDP，使 $∠ D C P = 90 °$ ，连接BD.设点P的运动时间为t秒.

(1)、 $△ A B C$ 中AB边上的高的长度为；

(2)、求BP的长（用含t的式子表示）；

(3)、当 $B P ： B D = 1 ： 2$ 时，直接写出t的值.

查看试题解析