吉林省白山市江源区三校名校调研系列卷2023-2024学年八年级上学期第三次月考试卷数学试卷
试卷更新日期：2023-12-06 类型：月考试卷
一、选择题（每小题2分，共12分）
-
1. 汉字是世界上最美的文字，形美如画、有的汉字是轴对称图形，下面四个汉字中是轴对称图形的是（ ）A、
B、
C、
D、
2. 若□×3ab =- 6a5b3 ，则□内应填的单项式是（ ）A、2a4b2 B、-2a4b2 C、-2a5b D、2a3b3. 如图，将一个五边形ABCDE沿虚线裁去一个角后得到的多边形ABCDGF的内角和为（ ）
A、180° B、360° C、540° D、720°4. 如图，在△ABC和△DEF中，点B、F、C、D在同一条直线上，已知∠A=∠D．AB=DE，添加下列条件，不能判定△ABC≌△DEF的是（ ）
A、EF=BC B、AC=DF C、∠ACB=∠DFE D、∠B=∠E5. 已知（x+m）（x-5）=x2-3x+k．则k，m的值分别是（ ）A、k=10，m=2 B、k=10，m=-2 C、k=-10，m=-2 D、k=-10，m=26. 如图，△ABC与△A1B1C1关于直线l对称，若∠B =25°，∠A=35°，则∠C的度数为（ ）
A、90° B、110° C、120° D、125°二、填空题（每小题3分，共24分）
-
7. 分解因式：8y2-y=8. 已知两根长度分别为3cm.7cm的木伟，若想钉一个等腰下角形木架，第三根木棒的长度应该是 cm．9. 若（a-2023）0=1，则a的取值范围是10. 如图，已知AD=DE，AB=BE，若∠A=75°，则∠CED =度．
11. 如图，在△ABC中，AB= AC，分别以点B和点C为圆心。以大于BC的长为半径作弧，两弧交于点D，作直线AD交BC于点E．若∠BAE=44°，则∠BAC=度．
12. 若am= 4，a2m+n= 128，则an=13. 如图，△ABC是等边三角形，AD∥BC，CD⊥AD．若AD =2cm，则AB=cm．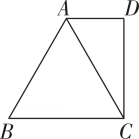
14. 如图，点D、E分别在等边△ABC的边AB、BC上，将△BDE沿直线DE翻折，使点B落在点B处，DB，、EB、分别交边AC于点F、G，若∠ADF =84°，则∠CEG=度．
三、解答题（每小题5分，共20分）
-
15. 化简：（x5）3+（-x4）2-（ x3）2·2x．16. 如图，点E在边AC上，CE =CB．∠A=∠D．∠DEC =∠ACB．求证：AB= CD．
17. 先化简，再求值：（x+3）2+（x+4）（x-4）+2x（2-x），其中x =18. 如图．在△ABC中，AD平分2 BAC交BC于点D，DF⊥AD交AB于点F，若∠B= 25°，∠C= 75° ，求证：△BFD是等腰三角形．
四、解答题（每小题7分，共28分）
-
19. 如图，点E在边BC上．AB与DE交于点F．DE= BC．∠AED =∠C．∠D=∠B．
(1)、求证：AE = AC；(2)、若∠DEB = 40° ，则∠C=度．20. 已知A、B均为整式，A= （xy+1）（xy-2）-2x2y2+2，小马在计算A÷B时，误把“÷”抄成了“-”，这样他计算的结果为-x2y2 ．
(1)、将整式A化为最简形式；(2)、求A÷B的正确结果．21. 如图。在△ABC中，DE、DF分别为BC、AB边的垂直平分线，连接AD、CD，
(1)、求证：DC = DA；(2)、若∠B=30°．AC=5，则△ACD的周长为22. 图①、图②均是由边长为1的小正方形组成的网格，每个小正方形的顶点称为格点，点A、B、C均在格点上．请用无刻度的直尺按下列要求在网格中作图．
(1)、在图①中，连接AC，以线段AC为腰作一个等腰直角三角形ACD；(2)、在图②中确定一个格点D，并画出以A、B、C、D为顶点的四边形．使其为轴对称图形．五、解答题（每小题8分，共16分）
-
23. 如图，从一个长和宽分别为x+2y，2x+y的长方形中剪下两个大小相同的边长为y的正方形（有关线段的长如图所示）。留下一个“T"型的图形（阴影部分）．
(1)、用含x、y的式子表示“T”型图形的面积并化简；(2)、若|y-3|+（x-2）2=0，请计算“T”型区域的面积．24. 如图，P为等边△ABC内一点，连接BP、PC，延长PC到点D，使CD= PC；延长BC到点E，使CE=BC，连接AE、DE．
(1)、求证：BP∥DE；(2)、求∠BAE的度数；(3)、若BP⊥AC，则∠AED=度．六、解答题（每小题10分，共20分）
-
25. [阅读理解]若x满足（32-x）（x-12） = 100，求（32-x）2+ （x-12）2的值。
解；设32-x=a．x-12= b，则（32-x）（x-12）= ab= 100，a+b= （32-x） +（x-12） = 20，（32-x）2+（x-12）2=a2+b2= （a+b）2- 2ab = 202-2×100=200．
我们把这种方法叫做换元法，利用换元法达到简化方程的目的，体现了转化的数学思想．
[解决问题]
(1)、若x满足（100-x）（x-95） = 5，则（100-x）2+（x-95）2 = ；(2)、若x满足（2023-x）2 +（x-2000）2 = 229 ，求（2023-x）（x-2000）的值；(3)、如图，在长方形ABCD中，AB = 24cm，点E、F是边BC、CD上的点，EC= 12cm，且BE = DF = xcm，分别以FC、CB为边在长方形ABCD外侧作正方形CFGH和CBMN，若长方形CBQF的面积为320cm2 ， 求图中阴影部分的面积和．
26. 如图．在正方形ABCD中，AB=BC=CD=DA=4．∠A=∠B=∠C=∠D=90°．动点P以每秒1个单位长度的速度从点B出发，沿线段BC方向运动，动点Q同时以每秒4个单位长度的速度从点A出发．沿正方形的边AD-DC-CB运动，当点P与点Q相遇时停止运动．设点P的运动时间为t秒．
(1)、运动时间为秒时，点P与点Q相遇；(2)、求t为何值时，△ABQ是等腰三角形？(3)、用含t的式子表示△AQP的面积S，并写出相应t的取值范围；(4)、连接PA，当以点Q及正方形的某两个顶点为顶点组成的三角形和△PAB全等时，直接写出t的值（点P与点Q重合时除外）．