吉林省白山市江源区三校名校调研系列卷2023-2024学年九年级上学期第三次月考数学试卷
试卷更新日期：2023-12-06 类型：月考试卷
一、选择题（每小题2分，共12分}
-
1. 下列图案中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
2. 若x=-2是一元二次方程x2+mx+2= 0的一个根，则m的值是（ ）A、-3 B、-2 C、2 D、33. 下列事件中，属于必然事件的是（ ）A、抛掷硬币时，正面朝上 B、小明发烧了，体温达到50℃ C、经过红绿灯路口，遇到红灯 D、任意写一个负数，小于正数4. 关于二次函数y=-（x-3）2+2的最值，下列说法正确的是（ ）A、有最大值3 B、有最小值3 C、有最大值2 D、有最小值25. 如图，在平面直角坐标系中，△ABC绕点C（0，1）旋转180°得到△A'B'C，已知点A的坐标为（2，-1）．则点A'的坐标是．（ ）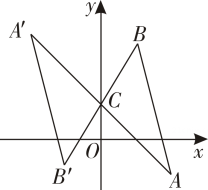
A、（- 2，1） B、（-2，3） C、（-2，-1） D、（-2，2）6. 如图，A、B、C是⊙O上的三个点，∠ABC=50°，连接AO、OC．过点O作OD⊥BC 于点D．若∠OCD=40°，则∠AOD的度数为（ ）．
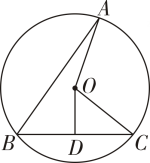A、120° B、135° C、140° D、150°二、填空题（每小题3分，共24分）
-
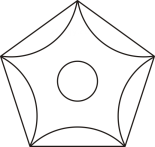
7. 方程x（4-x）=0的解为8. 抛物线y= （x-5）2+5的顶点坐标是9. 已知⊙O的半径为4cm，OP =2cm，则点P在⊙O（填“内"、“外”或“上”）．10. 如图，该图形绕其中心旋转能与自身完全重合．则其旋转角最小为度．
11. 将抛物线y=3（x-1）2+2向左平移3个单位长度，得到的新抛物线的解析式为12. 张师傅去华开了一家超市，今年2月份开始盈利，3月份盈利5000元，5月份盈利达到7200元，从3月到5月，设每月盈利的平均增长率都是x．则根据题意。可列方程：13. 如图．二次函数y=ax2+bx+c的图象与x轴交于点（3，0），对称轴是直线上x= 1．则当y<0时。自变量x的取值范围是
14. 如图，点C、D是⊙O上直径AB两侧的两点，若∠ACD= 60°．AB=8．则的长为 （结果保留π）．
三、解答题（每小题5分，共20分）
-
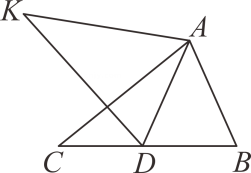
15. 解方街：x2+ 10x+24 = 3．16. 已知抛物线的顶点A（1，-4）．且经过点B（3，0）．求该抛物线的解析式：17. 如图，在△ABC中，AB=2，BC=3.6．∠B=60°，将△ABC绕点A按顺时针方向旋；转一定角度得到△ADK，当点B的对应点D恰好落在BC边上时，求CD的长．
18. 如图，AB是⊙O的一条弦，点C是AB的中点，连接OC并延长交于点D，连接OB、DB．若AB=4．CD=1．求△BOD的面积．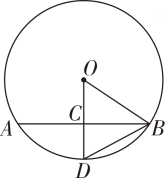
四、解答题{每小题7分，共28分}
-
19. 如图是四张不透明的卡片．除正面分别有数字1、1、2、3 外．其他均相间．将这四张卡肯面朝上洗匀后放置在桌面上．
(1)、小明从中随机抽取一张卡片，恰好得到数字1的概率是 ．(2)、小明和小丽恕用这四张卡片做游戏，游戏规则为小明先随机抽取一张卡片，小丽再从余下的卡片中随机抽取一张．如朵两张卡片上的数字和为奇数，小明胜；和为偶数，小丽胜．你认为这个游戏公平吗？请用列表或画树状图的方法说明理由．20. 光明中学准备在校园里利用围墙（墙长15m）和45m长的篱笆墙围建劳动实践基地．该校某数学兴趣小组设计了如下的围建方案（除围墙外，实线部分均为篱笆墙，且不浪费篱笆墙）：利用围墙和篱笆墙围成Ⅰ、Ⅱ两块矩形劳动实践基地，且在Ⅱ区中留一个宽度EH=1m的水池EFBH．已知CG=2DG．设DG的长度为xm．
(1)、AD的长度为m（用含x的代数式表示）；(2)、若劳动基地的总面积（不包含水池）为124m2 ， 求DG的长是多少？21. 如图。四边形ABCD内接于⊙O，BC为⊙O的直径。OA∥CD．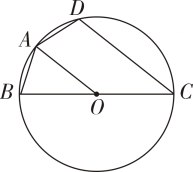
(1)、若∠ABC=70°，求∠BAD的度数；(2)、求证： ．22. 如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（-1，0）．B（-4，1）．C（-2，2）．
⑴直接写出点B关于原点O对称的点B1的坐标；
⑵请画出△ABC关于原点O成中心对称的△A2B2C2 ．
⑶画出△ABC绕点A逆时针旋转90°后得到的△AB3C3 ．
五、解答题{每小题8分，共16分}
-
23. 如图。AB是⊙O的直径，AP是⊙O的切线。点A为切点．BP与⊙O交于点C，点D是AP的中点。连接CD．
(1)、求证：CD是⊙O的切线：(2)、若AB=2，∠P=30°，求阴影部分的面积（结果保留根号和π）．24. 如图①．四边形ABCD与四边形AEFG是共一个顶点的两个大小不同的正方形．
(1)、操作发现：如图②．正方形AEFG绕顶点A逆时针旋转，使点E落在边AD上时．填空：①线段BE与IG的数量关系是
②∠ABE与∠ADG的关系是
(2)、猜想与证明：如图③，正方形AEFG绕顶点A逆时针旋转某一角度α（0<α< 90°）时．猜想（1）中的结论是否成立？并证明你的结论：(3)、拓展应用：如图④．正方形AEFG绕顶点A逆时针旋转，使点F落在边AD上时，若AB= ． AF=1，则BE=六、解答题（每小题10分，共20分）
-
25. 如图。在Rt△ABC中，∠C=90°．AC=BC，AB=4，点D为AB的中点．动点P从
点A出发沿线段AB以每秒1个单位长度的速度向终点B运动，点P关于点D中心对称的点为点Q．当点P与点D不重合时，以PQ为直角边向PQ上方作等腰直角△QPM．使∠QPM=90°．设点P的运动时间为t秒．
(1)、用含t的代数式表示线段PQ的长（直接写出）；(2)、当点M落在△ABC的边上时，求t的值；(3)、当△PQM与△ABC重叠部分为四边形时，求重叠部分的面积S与t之间的函数关系式．26. 如图，抛物线的顶点坐标为（2，6），且经过点（4，2）．点P是第一象限内的抛物线上的一点．且在对称轴右侧．过点P作PM⊥x轴于点M．PN⊥y轴于点N．设点P的横坐标为m．
(1)、求这条抛物线对应的函数解析式(2)、当四边形OMPN为正方形时，求m的值(3)、求四边形OMPN的周长的最大值(4)、若直线PN与这条抛物线的另一个交点为点Q，直接写出当时m的取值范围．