【北师大版·数学】2024年中考一轮复习之菱形的性质
试卷更新日期:2023-12-05 类型:一轮复习
一、选择题
-
1. 如图,在菱形中,点E在的延长线上, , , , 求的长( )
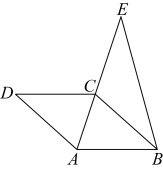 A、5 B、6 C、 D、2. 如图,某学校门口的伸缩门在伸缩的过程中,四边形始终是菱形,则下列结论不一定正确的是( )
A、5 B、6 C、 D、2. 如图,某学校门口的伸缩门在伸缩的过程中,四边形始终是菱形,则下列结论不一定正确的是( ) A、 B、 C、AB=AD D、AB=CD3. 如图,四边形为菱形, , , 则的长为( )
A、 B、 C、AB=AD D、AB=CD3. 如图,四边形为菱形, , , 则的长为( ) A、2 B、4 C、 D、4. 如图,在边长为4的菱形ABCD中,E为AD边的中点,连接CE交对角线BD于点F.若∠DEF=∠DFE,则这个菱形的面积为( )
A、2 B、4 C、 D、4. 如图,在边长为4的菱形ABCD中,E为AD边的中点,连接CE交对角线BD于点F.若∠DEF=∠DFE,则这个菱形的面积为( )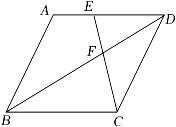 A、16 B、6 C、12 D、305. 如图,在菱形ABCD中,对角线AC、BD交于点O,已知AO=2,OB= , 则菱形ABCD的面积是( )
A、16 B、6 C、12 D、305. 如图,在菱形ABCD中,对角线AC、BD交于点O,已知AO=2,OB= , 则菱形ABCD的面积是( )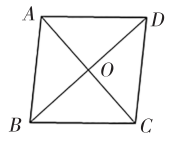 A、 B、 C、4 D、96. 如图,四边形是菱形,对角线、相交于点 , 过点作于点 , 连接 , , 则的度数是( )
A、 B、 C、4 D、96. 如图,四边形是菱形,对角线、相交于点 , 过点作于点 , 连接 , , 则的度数是( ) A、 B、 C、 D、7. 如图,菱形的两条对角线相交于点 , 若 , , 菱形的周长为( )
A、 B、 C、 D、7. 如图,菱形的两条对角线相交于点 , 若 , , 菱形的周长为( ) A、8 B、16 C、12 D、8. 如图,在边长为 的菱形 中, ,点E,F分别为折线 上的点(不含菱形顶点), , 、 相交于点G,作射线 .甲、乙二人分别对这个问题进行了研究:
A、8 B、16 C、12 D、8. 如图,在边长为 的菱形 中, ,点E,F分别为折线 上的点(不含菱形顶点), , 、 相交于点G,作射线 .甲、乙二人分别对这个问题进行了研究:甲:射线 不一定经过点C;
乙:当 垂直于菱形的边时,线段 的长可能为3.
下列判断正确的为( )
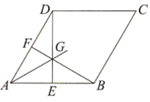 A、甲、乙都对 B、甲、乙都错 C、甲对,乙错 D、甲错,乙对9. 若菱形两条对角线的长度是方程x2﹣6x+8=0的两根,则该菱形的边长为( )A、 B、4 C、25 D、510. 如图,在平面直角坐标系中,菱形 的对称中心恰好是原点O , 已知点B坐标是 ,双曲线 经过点A , 则菱形 的面积是( )
A、甲、乙都对 B、甲、乙都错 C、甲对,乙错 D、甲错,乙对9. 若菱形两条对角线的长度是方程x2﹣6x+8=0的两根,则该菱形的边长为( )A、 B、4 C、25 D、510. 如图,在平面直角坐标系中,菱形 的对称中心恰好是原点O , 已知点B坐标是 ,双曲线 经过点A , 则菱形 的面积是( )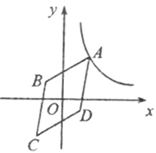 A、 B、18 C、 D、25
A、 B、18 C、 D、25二、填空题
-
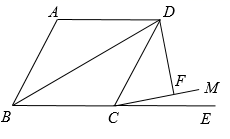
11. 已知菱形的两条对角线长分别为和 , 那么菱形的面积为 .12. 如图,四边形 为菱形, ,延长 到 ,在 内作射线 ,使得 ,过点 作 ,垂足为 ,若 ,则对角线 的长为.(结果保留根号)
 13. 如图,已知第个菱形中, , , 以对角线为边作第个菱形 , 使点在菱形的内部,且 , 再以对角线为边作第个菱形 , 使点在菱形的内部,且 , 顺次这样作下去 , 则第个菱形的面积为 .
13. 如图,已知第个菱形中, , , 以对角线为边作第个菱形 , 使点在菱形的内部,且 , 再以对角线为边作第个菱形 , 使点在菱形的内部,且 , 顺次这样作下去 , 则第个菱形的面积为 .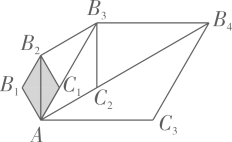 14. 如图,菱形的对角线与交于点O, , , 则 .
14. 如图,菱形的对角线与交于点O, , , 则 .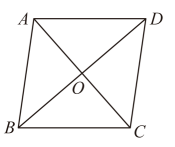 15. 在菱形中, , , 点在边上,连接 , 若 , 则线段的长为 .
15. 在菱形中, , , 点在边上,连接 , 若 , 则线段的长为 .三、作图题
-
16. 已知正六边形 , 请仅用无刻度的直尺完成下列作图(保留作图痕迹,不写作法,用虚线表示作图过程,实线表示作图结果).
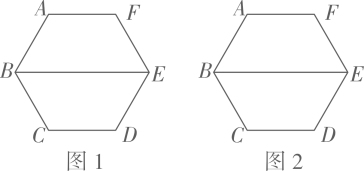 (1)、在图1中作出以为对角线的一个菱形;(2)、在图2中作出以为边的一个菱形 .
(1)、在图1中作出以为对角线的一个菱形;(2)、在图2中作出以为边的一个菱形 .四、解答题
-
17. 如图,四边形 是菱形,点 、 分别在边 、 的延长线上,且 .连接 、 .
求证: .
 18. 在如图菱形ABCD中,对角线AC、BD相交于O,E、F分别是AB、BC的中点.求证:OE=OF.
18. 在如图菱形ABCD中,对角线AC、BD相交于O,E、F分别是AB、BC的中点.求证:OE=OF.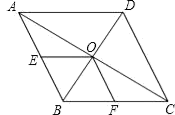
19. 已知:如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连结AE,AF.求证:AE=AF.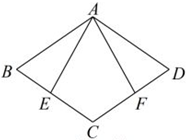 20. 如图,菱形ABCD中,E是对角线BD上的一点,连接EA、EC,求证:∠BAE=∠BCE.
20. 如图,菱形ABCD中,E是对角线BD上的一点,连接EA、EC,求证:∠BAE=∠BCE.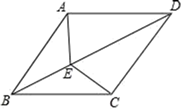
五、综合题
-
21. 已知线段a=4cm.
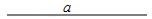 (1)、用尺规作图作一个边长为4cm的菱形ABCD,使∠A=60°(保留作图痕迹),(2)、求这个菱形的面积.22. 如图,在▱ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于 BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)、用尺规作图作一个边长为4cm的菱形ABCD,使∠A=60°(保留作图痕迹),(2)、求这个菱形的面积.22. 如图,在▱ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于 BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.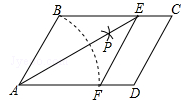 (1)、根据以上尺规作图的过程,求证:四边形ABEF是菱形;(2)、若菱形ABEF的周长为16,AE=4 ,求∠C的大小.23.
(1)、根据以上尺规作图的过程,求证:四边形ABEF是菱形;(2)、若菱形ABEF的周长为16,AE=4 ,求∠C的大小.23.邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,▱ABCD中,若AB=1,BC=2,则▱ABCD为1阶准菱形.
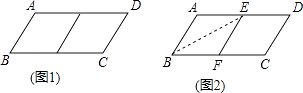 (1)、猜想与计算:
(1)、猜想与计算:邻边长分别为3和5的平行四边形是阶准菱形;已知▱ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出▱ABCD是阶准菱形.
(2)、操作与推理:小明为了剪去一个菱形,进行了如下操作:如图2,把▱ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.
-