【北师大版·数学】2024年中考一轮复习之勾股定理的应用

试卷更新日期：2023-12-05 类型：一轮复习

进入出卷网下载

一、选择题

1. 在《九章算术》中有一个问题（如图）：今有竹高一丈，末折抵地，去本三尺，问折者高几何？它的意思是：一根竹子原高一丈（10尺），中部一处折断，竹梢触地面处离竹根3尺，试问折断处离地面（）尺．

A、4 B、3.6 C、4.5 D、4.55

查看试题解析
2. 已知钓鱼杆AC的长为10米，露在水上的鱼线BC长为6m，某钓鱼者想看看鱼钩上的情况，把鱼竿AC 转动到ACˈ的位置，此时露在水面上的鱼线BʹCʹ 长度为8米，则BBʹ的长为( ）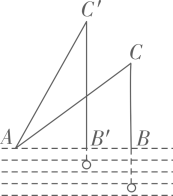

A、4米 B、3米 C、2米 D、1米

查看试题解析
3. 我国古代数学名著《九章算术》中记载：“今有竹高一丈、末折抵地，去本三尺 $.$ 问折者高几何？翻译：现有竹子高一丈，折断的末端撑着地，离地面竹根三尺远，问折断处离地面有多高？（1丈=10尺）设折断处离地的高度为 $x$ 尺，则下列方程正确的是（）

A、 $x^{2} + 3^{2} = (10 - x)^{2}$ B、 $x^{2} - 3^{2} = (10 - x)^{2}$ C、 $3^{2} + (10 - x)^{2} = x^{2}$ D、 $x^{2} + (10 - x)^{2} = 3^{2}$

查看试题解析
4. 如图，∠AOB=90°，OA=25m，OB=5m，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球，如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是（）.

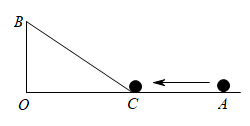A、12米 B、13米 C、14米 D、15米

查看试题解析
5. 如图，斜面AC的坡度（CD与AD的比）为1：2， $A C = 4 \sqrt{5}$ 米，坡顶有旗杆BC，旗杆顶端B点与A点有一条彩带相连，若AB=10米，则旗杆BC的高度为（）

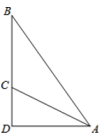A、2米 B、3米 C、 $（ 4 + \sqrt{5} ）$ 米 D、 $（ 2 + \sqrt{5} ）$ 米

查看试题解析
6. 我国古代数学著作《九章算术》中有这样一个问题：“今有方池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐.水深、葭长各几何？ ”.其大意是：如图，有一个水池，水面是一个边长为 10 尺 (丈、尺是长度单位，1 丈＝10 尺) 的正方形，在水池正中央有一根芦苇，它高出水面 1 尺.如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面.水的深度与这根芦苇的长度分别是多少？若设这跟芦苇的长度为 x 尺，根据题意，所列方程正确的是（）

A、10²＋(x－1)²＝x² B、10²＋(x－1)²＝ (x＋1)² C、5²＋(x－1)²＝x² D、5²＋(x－1)²＝ (x＋1)²

查看试题解析
7. 如图来自清朝数学家梅文鼎的《勾股举隅》，该图由四个全等的直角三角形围成，延长BC分别交AG，HG于点M，N，梅文鼎就是利用这幅图证明了勾股定理．若图中记△MNG的面积为S，△GDF的面积为9S，则阴影部分的面积为（）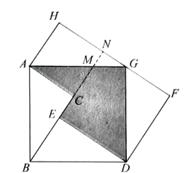

A、20S B、21S C、22S D、24S

查看试题解析
8. 勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再将较小的两个正方形分别绕直角三角形斜边上的两顶点旋转得到图2．则图2中阴影部分面积等于（）

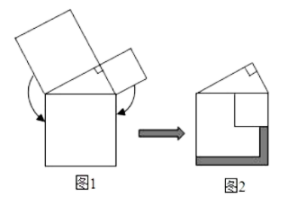A、直角三角形的面积 B、最大正方形的面积 C、最大正方形与直角三角形的面积和 D、较小两个正方形重叠部分的面积

查看试题解析
9. 如图，以正方形ABCD的边AD为直径作一个半圆，点M是半圆上一个动点，分别以线段AM、DM为边各自向外作一个正方形，其面积分别为S₁和S₂ ，若正方形的面积为10，随点M的运动S₁＋S₂的值（）

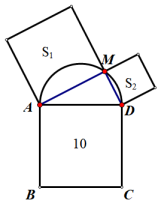A、大于10 B、小于10 C、等于10 D、不确定

查看试题解析
10. 如图，在△ABC中，AB＝AC，以点C为圆心，CB长为半径画弧，交AB于点B和点D，再分别以点B，D为圆心，大于 $\frac{1}{2}$ BD长为半径画弧，两弧相交于点M，作射线CM交AB于点E.若AE＝2，BE＝1，则EC的长度是（）

A、2 B、3 C、 $\sqrt{3}$ D、 $\sqrt{5}$

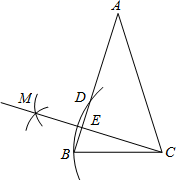查看试题解析

二、填空题

11. 刘徽是我国魏晋时期伟大的数学家，他在 $《$ 九章算术注 $》$ 中指出：“勾、股幂合为弦幂，明矣 $.$ ”也就是说，图 $1$ 中直角三角形的三边 $a$ 、 $b$ 、 $c$ 存在的关系 $.$ 他在书中构造了一些基本图形来解决问题 $.$ 如图 $2$ ，分别将以 $a$ 为边长的正方形和 $b$ 为边长的正方形置于以 $c$ 为边长的大正方形的左下角和右上角，则图中阴影部分面积等于 $($ 用含字母 $a$ 的代数式表示 $)$ ；若 $(c - a) (c - b) = 18$ ，则 $a + b - c =$ ．

查看试题解析
12. 我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”，后人称之为“赵爽弦图”，它是由4个全等的直角三角形和一个小正方形组成．如图，直角三角形的直角边长为a、b，斜边长为c，若 $b - a = 4 ， c = 20$ ，则每个直角三角形的面积为．

查看试题解析
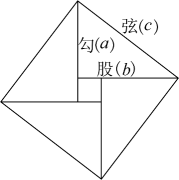13. 七巧板是古代中国劳动人民的发明，是一种古老的中国传统智力游戏，其历史至少可以追溯到公元前一世纪．小明将一个边长为4的正方形制作成一副如图1所示的七巧板，取出其中的六块，拼成了一个 $▱ A B C D$ （如图2），则 $▱ A B C D$ 的对角线AC的长度为．

查看试题解析
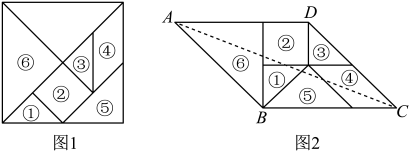14. 我国古代数学专著《九章算术》有这样一段文字“今有木长一丈，围之四尺，葛生其下，缠木六周，上与木齐，问葛几何？”题目大意为：现有一棵大树，高为 $1$ 丈，底面周长为 $4$ 尺，葛就生长在树下，缠绕了大树 $6$ 周，顶端与树一样齐，问葛有多长？葛为尺（ $1$ 丈 $= 10$ 尺）．

查看试题解析
15. 如图，三角形纸片 $A B C$ 中， $∠ B A C = 90 °$ ， $A B = 2$ ， $A C = 3$ ．沿过点A的直线将纸片折叠，使点B落在边 $B C$ 上的点D处；再折叠纸片，使点C与点D重合，若折痕与 $A C$ 的交点为E，则 $A E$ 的长是．

查看试题解析

三、作图题

16. 如图

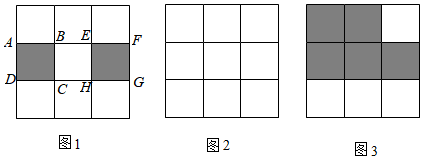(1)、如图1，在3×3的方格中，正方形ABCD，EFGH的边长均为1.求出正方形ABCD的对角线AC的长，并将正方形ABCD，EFGH剪拼成一个大正方形，在图2中画出示意图.

(2)、如图3，有5个小正方形（阴影部分），能剪拼成一个大正方形吗？若能，求出大正方形的边长；若不能，请说明理由.

查看试题解析
17. 在△ABC中，BC=a，AC=b，AB=c，若∠C=90°，如图1，则有 $a^{2} + b^{2} = c^{2}$ ；若△ABC为锐角三角形时，小明猜想： $a^{2} + b^{2} > c^{2}$ ，理由如下：如图2，过点A作AD⊥CB于点D，设CD=x．在Rt△ADC中， $A D^{2} = b^{2} - x^{2}$ ，在Rt△ADB中， $A D^{2} = c^{2} - {(a - x)}^{2}$ ，∴ $a^{2} + b^{2} = c^{2} + 2 a x$ ．
∵a＞0，x＞0，∴2ax＞0，∴ $a^{2} + b^{2} > c^{2}$ ，∴当△ABC为锐角三角形时 $a^{2} + b^{2} > c^{2}$ ．

所以小明的猜想是正确．

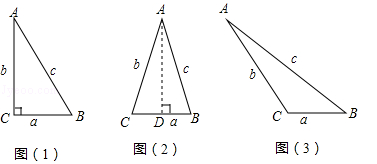(1)、请你猜想，当△ABC为钝角三角形时， $a^{2} + b^{2}$ 与 $c^{2}$ 的大小关系．

(2)、温馨提示：在图3中，作BC边上的高．

(3)、证明你猜想的结论是否正确．

查看试题解析
18. 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点。

(1)、在图1中以格点为顶点画一个面积为5的正方形；

(2)、在图2中以格点为顶点画一个三角形，使三角形三边长分别为2， $\sqrt{5}$ ， $\sqrt{13}$

查看试题解析

四、解答题

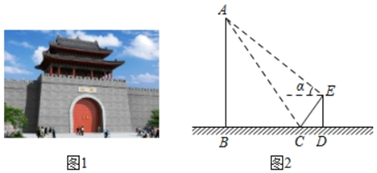
19. 如图1，是我区某村修建于清光绪年间的一座城门，某节假日随父亲回家的张菲同学想利用所学的数学知识测量此城门的高度.
如图2，她站在城门前方点D处，正好看到了城门顶端A点在地面小水潭（近似看成平面镜）里的倒影点C，此时他测得DC的长度为1米；接着她抬起头，目测城门顶端A点的仰角∠α的度数为39°，已知张菲同学的眼睛到地面的距离为1.5米，请你计算城门高度AB（结果精确到1米，sin39°≈0.63，cos39°≈0.78，tan39°≈0.81）.

查看试题解析
20. 图1是某种路灯的实物图片，图2是该路灯的平面示意图， $M N$ 为立柱的一部分，灯臂 $A C$ ，支架 $B C$ 与立柱 $M N$ 分别交于A，B两点，灯臂 $A C$ 与支架 $B C$ 交于点C，已知 $∠ M A C = 60 °$ ， $∠ A C B = 15 °$ ， $A C = 40 cm$ ，求支架 $B C$ 的长.（结果精确到 $1cm$ ，参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ， $\sqrt{6} \approx 2.449$ ）

查看试题解析
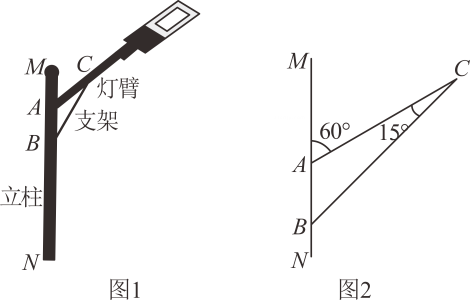21. 如图是一个可折叠的钢丝床的示意图，这是展开后支撑起来放在地面上的情况，如果折叠起来，床头部分被折到床面之上了（这里的A、B、C、D各点都是活动的）.活动床头是根据三角形的稳定性和四边形的不稳定性设计而成的，其折叠过程可用如图的变换反映出来，如果已知四边形ABCD中，AB=6，CD=15，那么BC、AD取多长时，才能实现上述的折叠变化？

查看试题解析
22. 鲁南高铁临沂段修建过程中需要经过一座小山．如图，施工方计划沿 $A C$ 方向开挖隧道，为了加快施工速度，要在小山的另一侧 $D$ ( $A$ 、 $C$ 、 $D$ 共线)处同时施工．测得 $∠ C A B = 30 °$ ， $A B = 4 k m$ ， $∠ A B D = 105 °$ ，求 $B D$ 的长．

查看试题解析

五、综合题

23. 如图，A，B是海面上位于东西方向的两个观测点，有一艘海轮在C点处遇险发出求救信号，此时测得C点位于观测点A的北偏东45°方向上，同时位于观测点B的北偏西60°方向上，且测得C点与观测点A的距离为 $25 \sqrt{2}$ 海里.

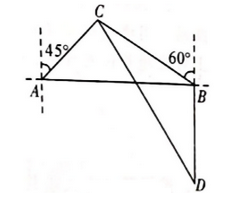(1)、求观测点B与C点之间的距离；

(2)、有一艘救援船位于观测点B的正南方向且与观测点B相距30海里的D点处，在接到海轮的求救信号后立即前往营救，其航行速度为42海里/小时，求救援船到达C点需要的最少时间.

查看试题解析
24. 某高速公路管理部门工作人员在对某段高速公路进行安全巡检过程中，发现该高速公路旁的一斜坡存在落石隐患．该斜坡横断面示意图如图所示，水平线 $l_{1} / / l_{2}$ ，点A、B分别在 $l_{1}$ 、 $l_{2}$ 上，斜坡AB的长为18米，过点B作 $B C ⊥ l_{1}$ 于点C，且线段AC的长为 $2 \sqrt{6}$ 米．

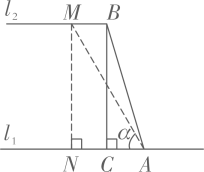(1)、求该斜坡的坡高BC；（结果用最简根式表示）

(2)、为降低落石风险，该管理部门计划对该斜坡进行改造，改造后的斜坡坡脚 $α$ 为60°，过点M作 $M N ⊥ l_{1}$ 于点N，求改造后的斜坡长度比改造前的斜坡长度增加了多少米？

查看试题解析
25. 如图，一艘船由A港沿北偏东60°方向航行10km至B港，然后再沿北偏西30°方向航行10km至C港。

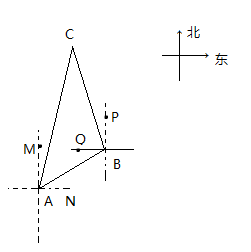(1)、求A，C两港之间的距离（结果保留到0.1km，参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）；

(2)、确定C港在A港的什么方向。

查看试题解析