【北师大版·数学】2024年中考一轮复习之二次函数的最值
试卷更新日期:2023-12-05 类型:一轮复习
一、选择题
-
1. 关于二次函数 的最大值或最小值,下列说法正确的是( )A、有最大值4 B、有最小值4 C、有最大值6 D、有最小值62. 抛物线y=x2+2x﹣3的最小值是( )A、3 B、﹣3 C、4 D、﹣43. 二次函数y=﹣(x﹣3)2+1的最大值为( )A、1 B、﹣1 C、3 D、﹣34. 定义符号min{a,b}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如:min={1,﹣2}=﹣2,min{﹣1,2}=﹣1.则min{x2﹣1,﹣2}的值是( )A、x2﹣1 B、2 C、﹣1 D、﹣25. 已知抛物线 的开口向下,顶点坐标为(2,-3),那么该二次函数有( )A、最小值-3 B、最大值-3 C、最小值2 D、最大值26. 已知抛物线 , 则当时,函数的最大值为( )A、 B、 C、0 D、27. 已知二次函数 , 当时,y的最小值为( )A、 B、 C、 D、78. 在平面直角坐标系中,设二次函数 , (a,b;是实数,)的最小值分别为m和n,若 , 则的值为( )A、0 B、 C、 D、9. 已知抛物线经过 , , 三点, . 当时,二次函数的最大值与最小值的差为16,则的值为( )A、-5 B、3 C、 D、410. 已知二次函数 , 关于该函数在的取值范围内有最大值-1,a可能为( )A、-2 B、-1 C、0.5 D、1.5
二、填空题
-
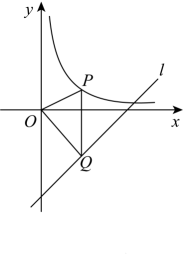
11. 如图,在直线:上方的双曲线上有一个动点 , 过点作轴的垂线,交直线于点 , 连接 , , 则面积的最大值是 .
 12. 我校办公楼前的花园是一道美丽的风景,现计划在花园里再加上一喷水装置,水从地面喷出,如图,以水平地面为x轴,出水点为原点建立平面直角坐标系,水在空中划出的曲线是抛物线(单位:米)的一部分,则水喷出的最大高度是米.
12. 我校办公楼前的花园是一道美丽的风景,现计划在花园里再加上一喷水装置,水从地面喷出,如图,以水平地面为x轴,出水点为原点建立平面直角坐标系,水在空中划出的曲线是抛物线(单位:米)的一部分,则水喷出的最大高度是米. 13. 公路上行驶的汽车急刹车时,刹车距离与时间的函数关系式为 , 当遇到紧急情况刹车时,由于惯性的作用,汽车要滑行 才能停下.14. 已知二次函数 , 当时,的最小值为 , 则的值为.15. 已知二次函数(、为常数,)的最大值为2,写出一组符合条件的和的值: .
13. 公路上行驶的汽车急刹车时,刹车距离与时间的函数关系式为 , 当遇到紧急情况刹车时,由于惯性的作用,汽车要滑行 才能停下.14. 已知二次函数 , 当时,的最小值为 , 则的值为.15. 已知二次函数(、为常数,)的最大值为2,写出一组符合条件的和的值: .三、解答题
-
16. 当k分别取﹣1,1,2时,函数y=(k﹣1)x2﹣4x+5﹣k都有最大值吗?请写出你的判断,并说明理由;若有,请求出最大值.17. 某架飞机着陆后滑行的距离单位:与滑行时间单位:近似满足函数关系 , 由电子监测获得滑行时间与滑行距离的几组数据如表:
滑行时间
滑行距离
(1)、根据上述数据,求出满足的函数关系;(2)、飞机着陆后滑行多远才能停下来?此时滑行的时间是多少?18. 对于“已知 , 求的最大值”这个问题,小明是这样求解的:∵ , ∴ , ∴
∴ , 所以的最大值为.
请你按照这种方法计算:当时,的最小值.
19. 某百货商店服装柜在销售中发现,某品牌童装平均每天可售出20件,每件盈利40元,经市场调查发现,在进货不变的情况下,若每件童装每降价1元,日销售量将增加2件.(1)、若想要这种童装销售利润每天达到1200元,同时又能让顾客得到更多的实惠,每件童装应降价多少元?(2)、当每件童装降价多少元时,这种童装一天的销售利润最多?最多利润是多少?20. 如图,抛物线 (a≠0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C , D在抛物线上.设A(t , 0),当t=2时,AD=4.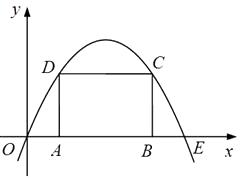 (1)、求抛物线的函数表达式.(2)、当t为何值时,矩形ABCD的周长有最大值?最大值是多少?(3)、保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G , H , 且直线GH平分矩形的面积时,求抛物线平移的距离.
(1)、求抛物线的函数表达式.(2)、当t为何值时,矩形ABCD的周长有最大值?最大值是多少?(3)、保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G , H , 且直线GH平分矩形的面积时,求抛物线平移的距离.四、综合题
-
21. 如图,在平面直角坐标系中,已知二次函数 , 顶点坐标为
(1)、若函数图象关于直线对称,求函数的表达式;
(2)、求的最大值;
(3)、是否存在实数 , 使得当时,二次函数的最大值为最小值的倍,若存在,求出;若不存在,请说明理由.22. 在二次函数中,(1)、若它的图象过点 , 则t的值为多少?(2)、当时,y的最小值为 , 求出t的值:(3)、如果都在这个二次函数的图象上,且 , 求m的取值范围。23. 傣族泼水节是流行于云南省傣族人民聚居地的传统节日,是国家级非物质文化遗产之一,又名“浴佛节”.泼水节临近,某超市销售某品牌塑料脸盆,进价为每只6元.在销售过程中发现,每天销售量(只)与每个售价(元)之间满足一次函数关系(其中 , 且为整数),当每只塑料脸盆的售价是8元时,每天销售量为100只;当每只塑料脸盆的售价是10元时,每天销售量为80只.(1)、求与之间的函数关系式;(2)、设超市销售该品牌塑料脸盆每天销售利润为元,当每只塑料脸盆的售价定为多少元时,超市销售该品牌塑料脸盆每天销售利润最大,最大利润是多少元?24. 宝珠梨盛产于昆明市呈贡区,是当地的特产水果,具有皮薄,果肉雪白,脆嫩,汁多,味浓甜,微香等特点.某果农经销某品牌的宝珠梨,成本为15元/千克.物价部门规定每千克梨的销售利润不得高于进价的 . 经市场调查发现:每天销售量y(单位:千克)与销售单价x(单位:元/千克)满足一次函数关系,部分图象如图所示: (1)、求y与x的函数解析式(解析式也称表达式).(2)、求这一天销售这种宝珠梨获得的最大利润W.25. 在锐角△ABC中,边BC长为18,高AD长为12
(1)、求y与x的函数解析式(解析式也称表达式).(2)、求这一天销售这种宝珠梨获得的最大利润W.25. 在锐角△ABC中,边BC长为18,高AD长为12 (1)、如图,矩形EFCH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K , 求 的值;(2)、设EH=x , 矩形EFGH的面积为S , 求S与x的函数关系式,并求S的最大值.
(1)、如图,矩形EFCH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K , 求 的值;(2)、设EH=x , 矩形EFGH的面积为S , 求S与x的函数关系式,并求S的最大值.