【北师大版·数学】2024年中考一轮复习之垂径定理的应用
试卷更新日期:2023-12-05 类型:一轮复习
一、选择题
-
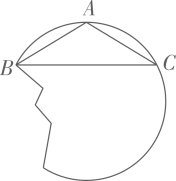
1. 如图所示为一名同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,厘米.若从目前太阳所处位置到太阳完全升出海平面的时间为16分钟,则“图上”太阳升起的速度为( ).
 A、1.0厘米/分 B、0.8厘米/分 C、12厘米/分 D、1.4厘米/分2. 如图所示,已知在5×5的正方形网格中,一条圆弧经过A,B,C三点,则这条圆弧所在圆的圆心是( ).
A、1.0厘米/分 B、0.8厘米/分 C、12厘米/分 D、1.4厘米/分2. 如图所示,已知在5×5的正方形网格中,一条圆弧经过A,B,C三点,则这条圆弧所在圆的圆心是( ).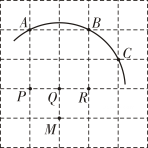 A、点P B、点Q C、点R D、点M3. 如图,排水管截面的半径为5分米,水面宽分米, , 则水的最大深度CD为( )
A、点P B、点Q C、点R D、点M3. 如图,排水管截面的半径为5分米,水面宽分米, , 则水的最大深度CD为( )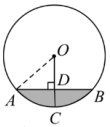 A、 B、 C、 D、4. 一条水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC的的长是( )
A、 B、 C、 D、4. 一条水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC的的长是( ) A、4 B、5 C、6 D、85. 下列命题:(1)垂直于弦的直线平分弦;(2)平分弦的直径必垂直于弦,并且平分弦所对的两条弧;(3)平分弦的直线必过圆心;(4)弦所对的两条弧的中点连线垂直平分弦。其中正确的命题有( )A、1个 B、2个 C、3个 D、4个6. 如图,“圆材埋壁”是我国古代著名数学著作九章算术中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何.”用几何语言可表述为:为的直径,弦于 , 寸,寸,则直径的长为( )
A、4 B、5 C、6 D、85. 下列命题:(1)垂直于弦的直线平分弦;(2)平分弦的直径必垂直于弦,并且平分弦所对的两条弧;(3)平分弦的直线必过圆心;(4)弦所对的两条弧的中点连线垂直平分弦。其中正确的命题有( )A、1个 B、2个 C、3个 D、4个6. 如图,“圆材埋壁”是我国古代著名数学著作九章算术中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何.”用几何语言可表述为:为的直径,弦于 , 寸,寸,则直径的长为( ) A、寸 B、寸 C、寸 D、寸7. 如图,点是上两点, , 点P是上的动点(P与不重合),连接 , 过点O分别作交于点E , 交于点F , 则等于( )
A、寸 B、寸 C、寸 D、寸7. 如图,点是上两点, , 点P是上的动点(P与不重合),连接 , 过点O分别作交于点E , 交于点F , 则等于( ) A、2 B、3 C、5 D、68. 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知 , 那么球的半径长是( )
A、2 B、3 C、5 D、68. 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知 , 那么球的半径长是( ) A、4 B、5 C、6 D、89. 如图所示的是一圆弧形拱门,其中路面AB=2m,拱高CD=3m,则该拱门的半径为( )
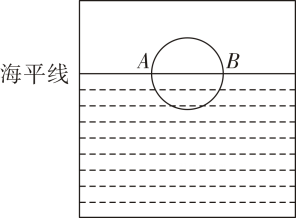
A、4 B、5 C、6 D、89. 如图所示的是一圆弧形拱门,其中路面AB=2m,拱高CD=3m,则该拱门的半径为( ) A、 B、2m C、 D、3m10. 如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( )
A、 B、2m C、 D、3m10. 如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( ) A、1.0厘米/分 B、0.8厘米/分 C、1.2厘米/分 D、1.4厘米/分
A、1.0厘米/分 B、0.8厘米/分 C、1.2厘米/分 D、1.4厘米/分二、填空题
-
11. 某市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如图所示,污水水面宽度为60 cm,水面至管道顶的距离为10 cm,则修理人员准备更换的新管道的内径为 .
 12. 《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中卷九中记载了一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”其意思是:如图,AB为⊙O的直径,弦CD⊥AB于点E , BE=1寸,CD=1尺,那么直径AB的长为多少寸?(注:1尺=10寸)根据题意,该圆的直径为寸.
12. 《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中卷九中记载了一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”其意思是:如图,AB为⊙O的直径,弦CD⊥AB于点E , BE=1寸,CD=1尺,那么直径AB的长为多少寸?(注:1尺=10寸)根据题意,该圆的直径为寸. 13. 已知直线m与半径为10cm的 O相切于点P,AB是 O的一条弦,且 = ,若AB=12cm,则直线m与弦AB之间的距离为.14. 如图,在⊙O中,直径EF⊥CD,垂足为M,若CD=2,EM=5,则⊙O的半径为.
13. 已知直线m与半径为10cm的 O相切于点P,AB是 O的一条弦,且 = ,若AB=12cm,则直线m与弦AB之间的距离为.14. 如图,在⊙O中,直径EF⊥CD,垂足为M,若CD=2,EM=5,则⊙O的半径为.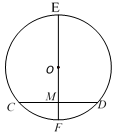 15. 一个学生荡秋千,秋千链子的长度为 ,当秋千向两边摆动时,摆角(指摆到最高位置时的秋千与铅垂线的夹角)恰好是 ,则它摆至最高位置时与其摆至最低位置时的高度之差为 m.(结果可以保留根号)
15. 一个学生荡秋千,秋千链子的长度为 ,当秋千向两边摆动时,摆角(指摆到最高位置时的秋千与铅垂线的夹角)恰好是 ,则它摆至最高位置时与其摆至最低位置时的高度之差为 m.(结果可以保留根号)三、解答题
-
16. 如图,已知AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为点E,BE=CD=16,试求⊙O的半径.
 17. 《九章算术》标志中国古代数学形成了完整的体系,第九卷《勾股》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言可表述为:“如图,是的直径,弦于点 , 寸,寸,求直径的长,”请你解答这个问题.
17. 《九章算术》标志中国古代数学形成了完整的体系,第九卷《勾股》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言可表述为:“如图,是的直径,弦于点 , 寸,寸,求直径的长,”请你解答这个问题. 18. 如图,已知 是 的外接圆,圆心O在 的外部, , ,求 的半径.
18. 如图,已知 是 的外接圆,圆心O在 的外部, , ,求 的半径.
四、综合题
-
19. 如图,是的直径,是上一点过点作于点 , 交于点 , 点是延长线上一点,连接 , , .
 (1)、求证:是切线;(2)、若 , , 求的长.
(1)、求证:是切线;(2)、若 , , 求的长.