【北师大版·数学】2024年中考一轮复习之三角形中位线定理
试卷更新日期:2023-12-05 类型:一轮复习
一、选择题
-
1. 在中, , , , 点 , , 分别为边 , , 的中点,则的周长为( )A、9 B、12 C、14 D、162. 如图,两点被池塘隔开,三点不共线.设的中点分别为 . 若米,则( )
 A、4米 B、6米 C、8米 D、10米3. 如图,在 中, ,点D,E分别为 , 的中点,则 ( )
A、4米 B、6米 C、8米 D、10米3. 如图,在 中, ,点D,E分别为 , 的中点,则 ( ) A、 B、 C、1 D、24. 如图,△ABC中,AB=10,AC=7,BC=9,点D、E、F分别是AB、AC、BC的中点,则四边形DBFE的周长是( )
A、 B、 C、1 D、24. 如图,△ABC中,AB=10,AC=7,BC=9,点D、E、F分别是AB、AC、BC的中点,则四边形DBFE的周长是( ) A、13 B、15 C、17 D、195. 如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )
A、13 B、15 C、17 D、195. 如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( ) A、24 B、14 C、12 D、66. 如图,在中, , D,E,F分别为 , , 的中点.若EF的长为10,则的长为( )
A、24 B、14 C、12 D、66. 如图,在中, , D,E,F分别为 , , 的中点.若EF的长为10,则的长为( ) A、5 B、10 C、15 D、207. 如图,在边长为的正方形中,对角线 , 相交于点 , 为线段的中点,连接 , 则线段的长为( )cm.
A、5 B、10 C、15 D、207. 如图,在边长为的正方形中,对角线 , 相交于点 , 为线段的中点,连接 , 则线段的长为( )cm. A、 B、 C、1 D、28. 如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.若AB=6,BC=8,则四边形BDEF的周长是( )
A、 B、 C、1 D、28. 如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.若AB=6,BC=8,则四边形BDEF的周长是( )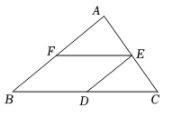 A、28 B、14 C、10 D、79. 如图,为测量B,C两地的距离,小娟在池塘外取点A,得到线段 , ,并取 , 的中点D,E,连结 .现测得 的长为6米,则B,C两地相距( )
A、28 B、14 C、10 D、79. 如图,为测量B,C两地的距离,小娟在池塘外取点A,得到线段 , ,并取 , 的中点D,E,连结 .现测得 的长为6米,则B,C两地相距( ) A、3米 B、6米 C、9米 D、12米10. 如图,在中,点D、E为边的三等分点,点F、G在边上, , 点H为与的交点.若 , 则的长为( )
A、3米 B、6米 C、9米 D、12米10. 如图,在中,点D、E为边的三等分点,点F、G在边上, , 点H为与的交点.若 , 则的长为( ) A、1 B、 C、2 D、3
A、1 B、 C、2 D、3二、填空题
-
11. 如图,已知在中, , , 点P是的中点,过点P的直线与交于点Q,依据尺规作图痕迹解决下列问题.
 (1)、与是否平行?(填“是”或“否”);(2)、的周长为 .12. 在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图所示,是格点三角形, , 与网格线分别交于 , 两点.若小正方形的边长为 , 则的长为 .
(1)、与是否平行?(填“是”或“否”);(2)、的周长为 .12. 在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图所示,是格点三角形, , 与网格线分别交于 , 两点.若小正方形的边长为 , 则的长为 . 13. 数学实践活动中,为了测量校园内被花坛隔开的A,B两点的距离,同学们在AB外选择一点C,测得AC, BC两边中点的距离DE为10m(如图),则A,B两点的距离是 m.
13. 数学实践活动中,为了测量校园内被花坛隔开的A,B两点的距离,同学们在AB外选择一点C,测得AC, BC两边中点的距离DE为10m(如图),则A,B两点的距离是 m. 14. 如图,在 中, , , 分别是边 , , 的中点,若 的周长为10,则 的周长为 .
14. 如图,在 中, , , 分别是边 , , 的中点,若 的周长为10,则 的周长为 .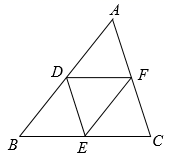 15. 如图,在中,点 , 分别是 , 的中点,若 , 则 .
15. 如图,在中,点 , 分别是 , 的中点,若 , 则 .
三、作图题
-
16. 图①、图②、图③分别是6×6的正方形网格,网格中每个小正方形的边长均为1,小正方形的顶点称为格点,点A、B、C、D、E、P、Q、M、N均在格点上,仅用无刻度的直尺在下列网格中按要求作图,保留作图痕迹.
 (1)、在图①中,画线段AB的中点F.(2)、在图②中,画△CDE的中位线GH,点G、H分别在线段CD、CE上,并直接写出△CGH与四边形DEHG的面积比.(3)、在图③中,画△PQR,点R在格点上,且△PQR被线段MN分成的两部分图形的面积比为1:3.17. 如图,在中, , 是的边上的中线,请用尺规作图法在边上求作一点 , 使得 . (不写作法,保留作图痕迹)
(1)、在图①中,画线段AB的中点F.(2)、在图②中,画△CDE的中位线GH,点G、H分别在线段CD、CE上,并直接写出△CGH与四边形DEHG的面积比.(3)、在图③中,画△PQR,点R在格点上,且△PQR被线段MN分成的两部分图形的面积比为1:3.17. 如图,在中, , 是的边上的中线,请用尺规作图法在边上求作一点 , 使得 . (不写作法,保留作图痕迹) 18. 如图,在由边长为1个单位长度的正方形组成的网格中,给出了格点(顶点为网格线的交点),请仅用无刻度直尺按下列要求作图(保留作图痕迹).
18. 如图,在由边长为1个单位长度的正方形组成的网格中,给出了格点(顶点为网格线的交点),请仅用无刻度直尺按下列要求作图(保留作图痕迹). (1)、请在网格①中,作的中位线PQ,交AB于点P,交BC于点Q.(2)、请在网格②中,作矩形ACMN,使
(1)、请在网格①中,作的中位线PQ,交AB于点P,交BC于点Q.(2)、请在网格②中,作矩形ACMN,使四、解答题
-
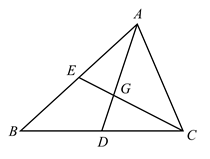
19. 三角形三条边上的中线交于一点,这个点叫三角形的重心.如图G是 的重心.求证: .
 20. 在△ABC中,点D、E、F分别是BC、AB、AC边的中点.求证:△BED≌△DFC.
20. 在△ABC中,点D、E、F分别是BC、AB、AC边的中点.求证:△BED≌△DFC. 21. 如图,在直角坐标系中,点A的坐标为(0,8),点 B(b,t)在直线x=b上运动,点D、E、F分别为OB、OA、AB的中点,其中b是大于零的常数.
21. 如图,在直角坐标系中,点A的坐标为(0,8),点 B(b,t)在直线x=b上运动,点D、E、F分别为OB、OA、AB的中点,其中b是大于零的常数. (1)、判断四边形DEFB的形状.并证明你的结论;(2)、试求四边形DEFB的面积S与b的关系式;(3)、设直线x=b与x轴交于点C,问:四边形DEFB能不能是矩形?
(1)、判断四边形DEFB的形状.并证明你的结论;(2)、试求四边形DEFB的面积S与b的关系式;(3)、设直线x=b与x轴交于点C,问:四边形DEFB能不能是矩形?若能.求出t的值;若不能,说明理由.
22.如图, 是 的中线, 是线段 上一点(不与点 重合). 交 于点 , ,连结 .
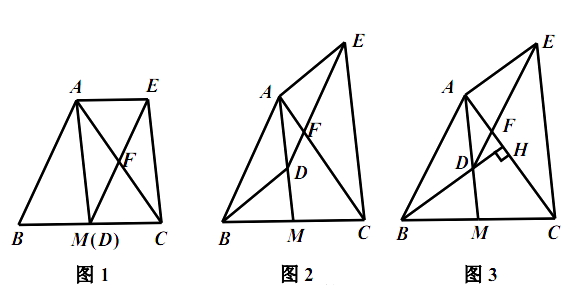 (1)、如图1,当点 与 重合时,求证:四边形 是平行四边形;(2)、如图2,当点 不与 重合时,(1)中的结论还成立吗?请说明理由.(3)、如图3,延长 交 于点 ,若 ,且 .
(1)、如图1,当点 与 重合时,求证:四边形 是平行四边形;(2)、如图2,当点 不与 重合时,(1)中的结论还成立吗?请说明理由.(3)、如图3,延长 交 于点 ,若 ,且 .①求 的度数;
②当 , 时,求 的长.
五、综合题
-
23. 如图,点E、F、G、H分别是各边的中点,连接相交于点M,连接相交于点N.
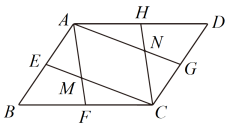 (1)、求证:四边形是平行四边形;(2)、若的面积为4,求的面积.24. 在平面直角坐标系中,已知点 , . 对于点给出如下定义:将点先向右或向左平移个单位长度,再向上或向下平移个单位长度,得到点 , 点关于点的对称点为 , 称点为点的“欢乐点”.
(1)、求证:四边形是平行四边形;(2)、若的面积为4,求的面积.24. 在平面直角坐标系中,已知点 , . 对于点给出如下定义:将点先向右或向左平移个单位长度,再向上或向下平移个单位长度,得到点 , 点关于点的对称点为 , 称点为点的“欢乐点”. (1)、如图,点 , 点在线段的延长线上.若点 , 点为点的“欢乐点”.
(1)、如图,点 , 点在线段的延长线上.若点 , 点为点的“欢乐点”.①在图中画出点与点;
②连接 , 交线段于点 , 求证:=;
(2)、⊙O的半径为1,是⊙O上一点,点在线段上,且=(<<1),若 为⊙O外一点,点为点P的“欢乐点”,连接 . 当点在⊙O上运动时,直接写出长的最大值与最小值的差(用含的式子表示).25. 如图1,在中, , 点D,E分别是的中点.把绕点B旋转一定角度,连结. (1)、如图2,当线段在内部时,求证:.(2)、当点D落在直线上时,请画出图形,并求的长.(3)、当面积最大时,请画出图形,并求出此时的面积.
(1)、如图2,当线段在内部时,求证:.(2)、当点D落在直线上时,请画出图形,并求的长.(3)、当面积最大时,请画出图形,并求出此时的面积.